
題目列表(包括答案和解析)
2.若向量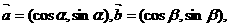 則
則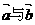 一定滿足( )
A.
一定滿足( )
A.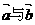 的夾角等于
的夾角等于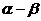 B.
B.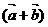 ⊥
⊥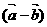
C.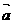 ∥
∥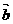 D.
D.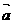 ⊥
⊥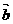
1.已知復數z1=1-i,z2=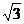 +i,則z=
+i,則z=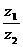 在復平面內對應點位于( )
在復平面內對應點位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
(15)(本小題滿分13分)
解關于x的不等式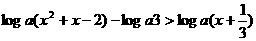 (a>0,a≠1)。
(a>0,a≠1)。
(16)(本小題滿分13分)
設函數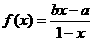 (x≠1,a>b)。
(x≠1,a>b)。
(I)求f(x)的反函數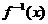 ;
;
(Ⅱ)判斷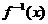 在(-b,+∞)上的單調性并用函數單調性定義加以證明。
在(-b,+∞)上的單調性并用函數單調性定義加以證明。
(17)(本小題滿分14分)
某旅游點有50輛自行車供游客租賃使用,管理這些自行車的費用為每日115元。根據經驗,若每輛自行車的日租金不超過6元,則自行車可以全部租出;若超過6元,則每超過1元,租不出去的自行車就增加3輛。
為了便于結算,每輛自行車的日租金x(元)只取整數,并且要求出租自行車一日總收入必須高于這一日的管理費用,用y(元)表示出租自行車的日凈收入(即一日中出租自行車的總收入減去管理費后的所得)。
(I)求函數y = f(x)的解析式及其定義域;
(Ⅱ)試問當每輛自行車的日租金定為多少元時,才能使一日的凈收入最多?
(必要時可參考以下數據: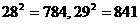 )。
)。
(18)(本小題滿分14分)
如圖,AB是圓O的直徑,PA垂直于圓O所在的平面,C是圓周上的一點,若A在PC,PB上的射影為D、E。
(Ⅰ)求證:AD⊥平面PBC;
(Ⅱ)若PA=AB=2,∠BPC=θ,試用tgθ表示△ADE的面積,當tgθ取何值時,△ADE面積最大,最大面積是多少?
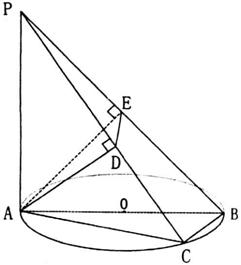
第(18)題圖
(19)(本小題滿分15分)
已知拋物線方程為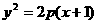 (p >0),直線l:x+y=m過拋物線的焦點F且被拋物線截得的弦長為3。
(p >0),直線l:x+y=m過拋物線的焦點F且被拋物線截得的弦長為3。
(Ⅰ)求p的值;
(Ⅱ)是否存在點M,使過點M的斜率不為零的任意直線與拋物線交于P、Q兩點,并且以PQ為直徑的圓恰過拋物線的頂點?若存在,求出M點的坐標;若不存在,請說明理由。
(20)(本小題滿分15分)
若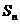 和
和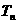 分別表示數列
分別表示數列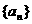 和
和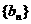 的前n項的和,對任意正整數n,
的前n項的和,對任意正整數n,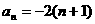 ,
,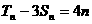 。
。
(Ⅰ)求數列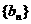 的通項公式;
的通項公式;
(Ⅱ)在平面直角坐標系內,直線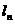 的斜率為
的斜率為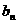 ,且與曲線
,且與曲線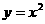 有且僅有一個交點,與y軸交于點
有且僅有一個交點,與y軸交于點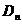 ,記
,記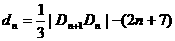 ,求
,求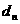 ;
;
(Ⅲ)若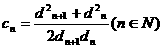 ,求證:
,求證: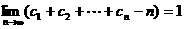 。
。
(11)已知橢圓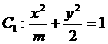 與
與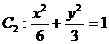 有相同的離心率e,那么m的值為___________.
有相同的離心率e,那么m的值為___________.
(12)設等差數列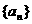 的前n項和為
的前n項和為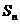 ,若
,若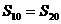 ,則
,則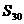 的值是_________。
的值是_________。
(13)如圖,直三棱柱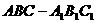 中,P、Q分別是側棱
中,P、Q分別是側棱 、
、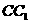 上的點,且
上的點,且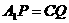 ,則四棱錐
,則四棱錐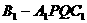 的體積與多面體
的體積與多面體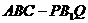 的體積的比值為________。
的體積的比值為________。
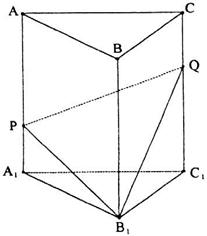
第(13)題圖
(14)已知函數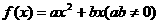 ,若
,若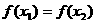 ,且
,且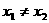 ,那么
,那么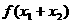 的值是_______________。
的值是_______________。
(1)下列集合中表示空集的是
(A){0} (B)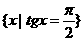
(C){x | ctgx = 0} (D)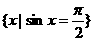
(2)(理)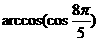 的值是
的值是
(A)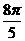 (B)
(B)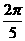
(C)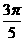 (D)
(D)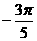
(文)已知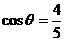 ,
,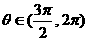 ,那么ctgθ的值等于
,那么ctgθ的值等于
(A)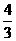 (B)
(B)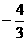
(C)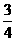 (D)
(D)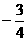
(3)已知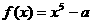 ,且f(-1)=0,那么
,且f(-1)=0,那么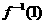 的值是
的值是
(A)0 (B)1
(C)-1 (D)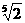
(4)(理)已知點A,B的極坐標分別是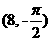 ,(8,
,(8,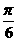 ),那么線段AB的中點C的極坐標可以是
),那么線段AB的中點C的極坐標可以是
(A)(4,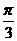 ) (B)(4,
) (B)(4,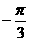 )
)
(C)(4,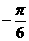 ) (D)(4,
) (D)(4,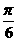 )
)
(文)若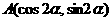 ,
,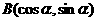 ,則A,B兩點間的距離為
,則A,B兩點間的距離為
(A)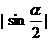 (B)
(B)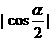
(C)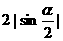 (D)
(D)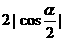
(5)將一張坐標紙折疊一次,使得點(0,2)與(-2,0)重合,且點(2002,2003)與點(m,n)重合,則m-n 的值為
(A)1 (B)-1
(C)0 (D)-2
(6)已知直線a、b和平面M、N,且a⊥M,那么
(A)b∥M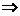 b⊥a (B)b⊥a
b⊥a (B)b⊥a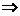 b∥M
b∥M
(C)N⊥M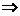 a∥N (D)
a∥N (D)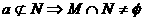
(7)從不同品牌的4臺快譯通和不同品牌的5臺錄音筆中任意抽取3臺,其中至少要有快譯通知錄音筆各1臺,則不同的取法共有
(A)140種 (B)84種
(C)70種 (D)35種
(8)若復數z與它的共軛復數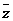 滿足
滿足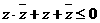 ,
,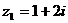 ,則
,則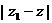 的最大值是
的最大值是
(A)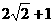 (B)
(B)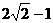
(C)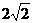 (C)2
(C)2
(9)若當P(m,n)為圓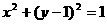 上任意一點時,不等式m+n+c≥0恒成立,則c的取值范圍是
上任意一點時,不等式m+n+c≥0恒成立,則c的取值范圍是
(A)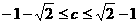 (B)
(B)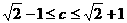
(C)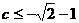 (D)
(D)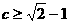
(10)已知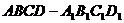 是棱長為a的正方體,P是
是棱長為a的正方體,P是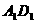 上的定點,Q是
上的定點,Q是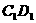 上的動點,長為b(b是常數,0 < b < a)的線段EF在棱AB上滑動,那么四面體PQEF的體積是
上的動點,長為b(b是常數,0 < b < a)的線段EF在棱AB上滑動,那么四面體PQEF的體積是
(A)常量 (B)變量且有最大值
(C)變量且有最小值 (C)變量且有最大值也有最小值
第Ⅱ卷(非選擇題共100分)
22.(2003年高考江蘇卷21)(本小題滿分12分)
已知 為正整數.
為正整數.
(Ⅰ)設 ;
;
(Ⅱ)設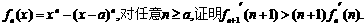
本小題主要考查導數、不等式證明等知識,考查綜合運用所數學知識解決問題的能力,滿分12分.
證明:(Ⅰ)因為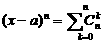
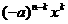 ,
,
所以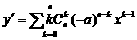
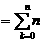
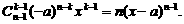
(Ⅱ)對函數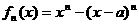 求導數:
求導數:
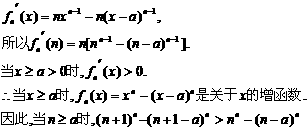
∴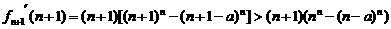
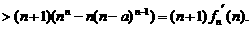
即對任意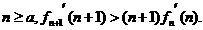
21.某商場預計全年分批購入每臺價值為2000元的電視機共3600臺。每批都購入x臺,且每批均需付運費400元;貯存購入的電視機全年所付保管費與每批購入電視機的總價值(不含運費)成正比;若每批購入400臺,則全年需用去運輸和保管總費用43600元。現在全年只有24000元資金可以用于支付這筆費用。請問:能否恰當安排每批進貨的數量使資金夠用。寫出你的結論,并說明理由。
解:設每批購入x臺,由題意,全年需用保管費為 元;設全年運輸和保管總費用為y元,則
元;設全年運輸和保管總費用為y元,則
 。
。
由已知當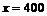 時,
時,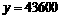 ,代入上式解之得
,代入上式解之得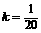
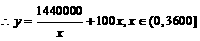
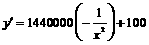 ,令
,令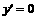 ,解之得
,解之得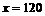 (臺)
(臺)
將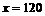 (臺)代入,
(臺)代入,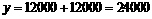 (元)
(元)
結果說明,只有安排每批進貨120臺,才能使所購資金夠用。
20.(2003年高考全國卷-理19)(本小題滿分12分)
已知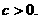 設
設
P:函數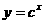 在R上單調遞減.
在R上單調遞減.
Q:不等式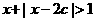 的解集為R,如果P和Q有且僅有一個正確,求
的解集為R,如果P和Q有且僅有一個正確,求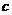 的取值范圍.
的取值范圍.
解:函數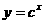 在R上單調遞減
在R上單調遞減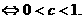
不等式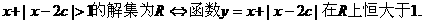

19.(2003年高考天津卷-理19)(本小題滿分12分)
設 ,求函數
,求函數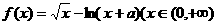 的單調區間.
的單調區間.
本小題主要考查導數的概念和計算,應用導數研究函數性質的方法及推理和運算能力. 滿分12分.
解: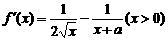 .
.
當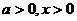 時
時 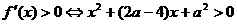 .
.
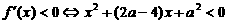
(i)當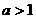 時,對所有
時,對所有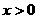 ,有
,有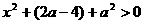 .
.
即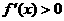 ,此時
,此時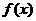 在
在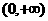 內單調遞增.
內單調遞增.
(ii)當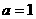 時,對
時,對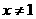 ,有
,有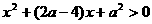 ,
,
即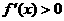 ,此時
,此時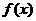 在(0,1)內單調遞增,又知函數
在(0,1)內單調遞增,又知函數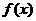 在x=1處連續,因此,
在x=1處連續,因此,
函數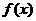 在(0,+
在(0,+ )內單調遞增
)內單調遞增
(iii)當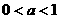 時,令
時,令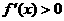 ,即
,即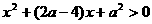 .
.
解得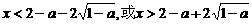 .
.
18.(2003年高考上海卷-理19)(本題滿分14分)本題共有2個小題,第1小題滿分5分,第2小題滿分9分.
已知數列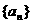 (n為正整數)是首項是a1,公比為q的等比數列.
(n為正整數)是首項是a1,公比為q的等比數列.
(1)求和: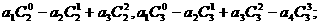
(2)由(1)的結果歸納概括出關于正整數n的一個結論,并加以證明.
[解](1)
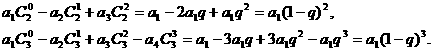
(2)歸納概括的結論為:
若數列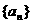 是首項為a1,公比為q的等比數列,則
是首項為a1,公比為q的等比數列,則
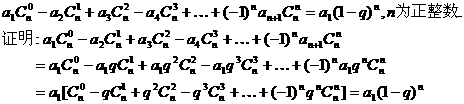
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com