
題目列表(包括答案和解析)
6.求分別滿(mǎn)足下列條件的直線(xiàn)l的方程:
(1)直線(xiàn)l過(guò)點(diǎn)A(1,-2),且點(diǎn)B(2,1)到l的距離等于1;
(2)過(guò)點(diǎn)M(-1,2)作直線(xiàn)l,使點(diǎn)A(-3,4)和B(1,-2)到l的距離相等;
(3)直線(xiàn)l過(guò)點(diǎn)P(-3,4),且在兩坐標(biāo)軸上的截距相等.
5.已知直線(xiàn)ax+3y+1=0與直線(xiàn)x+(a-2)y+a=0,當(dāng)a=_________時(shí),兩直線(xiàn)平行;當(dāng)a=_________時(shí),兩直線(xiàn)重合;當(dāng)a∈_________時(shí),兩直線(xiàn)相交.
4.已知兩點(diǎn)A(cos70°,cos20°)、B(sin80°,sin10°),則直線(xiàn)AB的傾斜角是_________.
3.點(diǎn)M(1,3),N(5,-2),點(diǎn)P在x軸上,使|PM|-|PN|取最大值的點(diǎn)P的坐標(biāo)為
A.(4,0) B.(13,0)
C.(5,0) D.(1,0)
2.如果AC<0,且BC<0,那么直線(xiàn)Ax+By+C=0不通過(guò)
A.第一象限 B.第二象限
C.第三象限 D.第四象限
1.下列命題中是真命題的是
A.經(jīng)過(guò)定點(diǎn)P0(x0,y0)的直線(xiàn)都可以用方程y-y0=k(x-x0)表示
B.經(jīng)過(guò)任意兩個(gè)不同的點(diǎn)P1(x1,y1)、P2(x2,y2)的直線(xiàn)都可以用方程(y-y1)(x2-x1)=(x-x1)(y2-y1)表示
C.不經(jīng)過(guò)原點(diǎn)的直線(xiàn)都可以用方程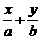 =1表示
=1表示
D.經(jīng)過(guò)定點(diǎn)A(0,b)的直線(xiàn)都可以用方程y=kx+b表示
(三)解答題
20.正方形中心為G(-1,0),一邊所在直線(xiàn)的斜率為3,且此正方形的面積為14.4,求這正方 形各邊所在直線(xiàn)的方程.
21.已知在△ABC的邊上運(yùn)動(dòng)的點(diǎn)D、E、F在t=0時(shí)分別從A、B、C出發(fā),各以一定的速度向B、 C、A前進(jìn),在t=1時(shí)分別達(dá)到B、C、A,試證明在運(yùn)動(dòng)過(guò)程中,△DEF的重心是一個(gè)定點(diǎn).
22.一條光線(xiàn)從點(diǎn)M(5,3)射出,被直線(xiàn)l∶x+y=1反射,入射光線(xiàn)到直線(xiàn)l的角為β,已知tgβ=2,求入射光線(xiàn)與反射光線(xiàn)所在直線(xiàn)的方程.
23.用解析法證明三角形內(nèi)角平分線(xiàn)性質(zhì)定理.
24.已知點(diǎn)P(6,8),過(guò)P點(diǎn)作直線(xiàn)PA⊥PB分別交x軸正半軸、y軸正半軸于A、B兩點(diǎn)。
①求線(xiàn)段AB的中點(diǎn)的軌跡。
②若△AOB面積等于△APB面積,求此時(shí)直線(xiàn)PA與直線(xiàn)PB的方程。
25.已知?jiǎng)狱c(diǎn)P(x,y)在以A(π,0)、B(-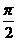 ,-
,-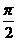 )為兩端點(diǎn)的線(xiàn)段上移動(dòng),且sinx+sin2y=0。求點(diǎn)P的坐標(biāo)。
)為兩端點(diǎn)的線(xiàn)段上移動(dòng),且sinx+sin2y=0。求點(diǎn)P的坐標(biāo)。
(二)填空題
16.兩條平行直線(xiàn)2x-7y+8=0和2x-7y-8=0間的距離是 .
17.如果直線(xiàn)l1、l2的斜率分別是二次方程x2-4x+1=0的兩根,那么l1與l2所成 角的大小是 .
18.直線(xiàn)y=-x+b和5x+3y-31=0的交點(diǎn)在第一象限,那么b的范圍是 .
19.已知點(diǎn)P是直線(xiàn)l上一點(diǎn),將直線(xiàn)l繞點(diǎn)P沿逆時(shí)針?lè)较蛐D(zhuǎn)角α(0°<α<90°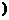 ,所得直 線(xiàn)的方程是x-y-2=0,若將它繼續(xù)為轉(zhuǎn)90°-α,所得直線(xiàn)的方程2x+y-1=0,則直線(xiàn)l的方程為
.
,所得直 線(xiàn)的方程是x-y-2=0,若將它繼續(xù)為轉(zhuǎn)90°-α,所得直線(xiàn)的方程2x+y-1=0,則直線(xiàn)l的方程為
.
(一)選擇題
1.直線(xiàn)Ax+By+C=0通過(guò)第一、二、三象限,當(dāng)且僅當(dāng)( )
A.A·B>0,A·C>0 B.A·B>0,A·C<0
C.A·B<0,A·C>0 D.A·B<0,A·C<0
2.已知點(diǎn)M(3,4),N(12,7),P在直線(xiàn)MN上,且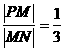 ,則點(diǎn)P的坐標(biāo)是( )
,則點(diǎn)P的坐標(biāo)是( )
A.(6,5) B.(9,6)
C.(0,3) D.(0,3)或(6,5)
3.已知點(diǎn)A(3,3),B(-1,5),直線(xiàn)y=ax+1與線(xiàn)段AB有公共點(diǎn),則實(shí)數(shù)a應(yīng)滿(mǎn)足的條件是( )
A.a∈[-4,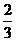 ]
B.a≠-
]
B.a≠-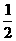
C.a∈[-4,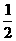 ]∪(-
]∪(-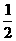 ,
,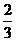 )
D.a∈(-∞,-4)∪(
)
D.a∈(-∞,-4)∪(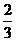 ,+∞]
,+∞]
4.方程│x-1│+y=1確定的曲線(xiàn)與x軸圍成的圖形的面積是( )
A. 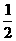 B.1 C.2 D.4
B.1 C.2 D.4
5.過(guò)點(diǎn)(2,3)且在兩坐標(biāo)軸上截距相等的直線(xiàn)方程是( )
A.x+y=5 B.3x-2y=0
C.x+y=5或3x-2y=0 D.4x-y=5
6.直線(xiàn)l過(guò)點(diǎn)P(3,2),與x軸、y軸的正半軸交于A、B兩點(diǎn),O是坐標(biāo)原點(diǎn),當(dāng)△AOB面積為最 小值時(shí),直線(xiàn)l的方程是( )
A.x-y-1=0 B.x+y-5=0
C.2x+3y-12=0 D.3x+2y-13=0
7.如果直線(xiàn)Ax+By+C=0的傾斜角是一銳角,且在y軸上的截距大于零,則( )
A.AB>0,AC>0 B.AB>0,AC<0
C.AB<0,AC>0 D.AB<0,AC<0
8.下列各點(diǎn)中,不與P(4,3)、Q(-1,6)兩點(diǎn)共線(xiàn)的點(diǎn)是( )
A.(5,6) B.(2,-3)
C.(3t,t+3)(這里t∈Z) D.(t+3,3t)(這里t∈Z)
9.兩條不重合的直線(xiàn)mx+y-n=0和x+my+1=0互相平行的充要條件是( )
A.m=1,n=1 B.m=-1,n=-1
C.m=1,n≠-1,或m=-1,n≠1 D.m≠±1,n≠±1
10.與直線(xiàn)2x+3y-6=0關(guān)于點(diǎn)(1,-1)對(duì)稱(chēng)的直線(xiàn)是( )
A.3x-2y+2=0 B.2x+3y+1=0
C.3x-2y-12=0 D.2x+3y+8=0
11.已知0≤θ≤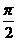 ,且點(diǎn)(1,cosθ) 到直線(xiàn)xsinθ+ycosθ=1的距離等于
,且點(diǎn)(1,cosθ) 到直線(xiàn)xsinθ+ycosθ=1的距離等于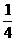 ,則θ等于( )
,則θ等于( )
A. 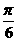 B.
B. 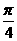 C.
C. 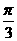 D.
D. 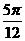
12.已知直線(xiàn)l1∶x-2y-6=0,l2∶3x-y+4=0下列說(shuō)法中錯(cuò)誤的是( )
A.l1與l2的夾角是45° B.l1到l2的角是45°
C.l2到l1的夾角是45° D.l2到l1的角是135 °
13.若a2+b2=c2,則直線(xiàn)ax+by+c=0被圓x2+y2=2所截的弦長(zhǎng)等于( )
A.1
B.2 C.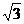 D.2
D.2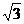
14.△ABC中,B(-a,0)、C(a,0),且兩底角的正切的乘積為定值k(k>0),則頂點(diǎn)A的軌跡方 程是( )
A.kx2+y2=ka2(y≠0) B.kx2-y2=ka2(y≠0)
C.x2+ky2=ka2(y≠0) D.x2-ky2=ka2(y≠0)
15.設(shè)點(diǎn)A(-1,2),B(2,-2),C(0,3),且M(a,b)是線(xiàn)段AB上的一點(diǎn)(a≠0),則直線(xiàn)MC的 斜率的取值范圍是( )
A.[-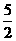 ,1]
B.[-1,
,1]
B.[-1, 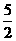 ]
]
C.[-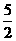 ,0]∪(0,1)
D.(-∞ ,-
,0]∪(0,1)
D.(-∞ ,-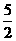 )∪(1,+∞)
)∪(1,+∞)
(四)綜合例題賞析
例4設(shè)點(diǎn)P在有向線(xiàn)段AB的延長(zhǎng)線(xiàn)上,P分AB所在的比為λ,則 ( )
A.λ<-1 B.-1<λ<0
C.0<λ<1 D.λ>1
解 由已知有λ=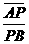 因?yàn)?sub>
因?yàn)?sub>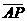 與
與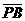 的方向相反,且|
的方向相反,且|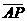 |>|
|>|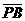 |,
|,
所以λ=?|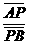 |<-1,
|<-1,
應(yīng)選A。
例5 和直線(xiàn)3x-4y+5=0關(guān)于x軸對(duì)稱(chēng)的直線(xiàn)方程是( )
A.3x+4y-5=0 B.3x+4y+5=0
C.-3x+4y-5=0 D.-3x+4y+5=0
解: 若曲線(xiàn)c的方程f(x,y)=0,曲線(xiàn)c和c′關(guān)于x軸對(duì)稱(chēng),則曲線(xiàn)c′的方程是f(x,-y)=0.
∴3x-4(-y)+5=0即3x+4y+5=0為所求.
應(yīng)選B.
例6 如圖,設(shè)圖中直線(xiàn)l1,l2,l3的斜率分 別為k1,k2,k3,則( )
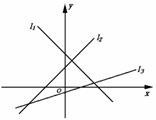
A.k1<k2<k3 B.k3<k1<k2
C.k3<k2<k1 D.k1<k1<k2
解 顯然k1<0,0<k3<k2
于是應(yīng)選D.
例7 如果直線(xiàn)y=ax+2與直線(xiàn)y=3x-b關(guān)于直線(xiàn)y=x對(duì)稱(chēng),那么( )
A.a=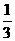 ,b=6
B.a=
,b=6
B.a=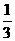 ,b=-6 C.a=3,b=-2
D.a=3,b=6
,b=-6 C.a=3,b=-2
D.a=3,b=6
解 C1的方程是f(x,y)=0,C2和C1關(guān)于直線(xiàn)y=x對(duì)稱(chēng),則C2的方程是f(y,x)=0.
于是直線(xiàn)y=ax+2關(guān)于直線(xiàn)y=x對(duì)稱(chēng)的直線(xiàn)的方程是x=ay+2,即y=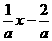 .
.
由題設(shè)y=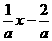 和y=3x-b是同一條直線(xiàn),
和y=3x-b是同一條直線(xiàn),
所以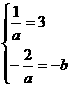 ,解得
,解得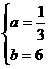
從而應(yīng)選A.
例8 通過(guò)點(diǎn)(0,2)且傾斜角為15°的直線(xiàn)方程是( )
A.y=(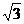 -2)x+2
B.y=(
-2)x+2
B.y=(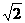 -1)x+2
-1)x+2
C.y=(2-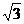 )x+2
D.y=(
)x+2
D.y=(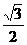 -1) x+2
-1) x+2
解: ∵直線(xiàn)通過(guò)點(diǎn)(0,2).
∴直線(xiàn)在y軸上的截距b=2.
∵直線(xiàn)的傾角為15°,
∴直線(xiàn)的斜率k=tg15°=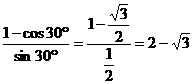 .
.
把k=2-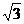 ,b=2代入直線(xiàn)的斜截式方程y=kx+b,得y=(2-
,b=2代入直線(xiàn)的斜截式方程y=kx+b,得y=(2-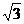 )x+2 .
)x+2 .
應(yīng)選C.
例9 直線(xiàn)3x-2y=6在y軸上的截距是( )
A.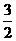 B.-2 C. -3 D.3
B.-2 C. -3 D.3
解: ∵3x-2y=6 y=-
y=-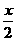 +
+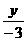 =1,
=1,
又直線(xiàn)的截距為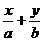 =1,
=1,
∴b=-3,即在y軸上的截距為-3.
應(yīng)選C.
例10 如果直線(xiàn)ax+2y+2=0與直線(xiàn)3x-y-2=0平行,那么 系數(shù)a=( )
A.-3
B.-6 C.-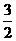 D.
D. 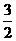
解:l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0,且A2≠0,B2≠0,C2≠ 0,則有
l1∥l2
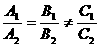
∴由題設(shè)有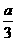 =
=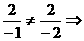 a=- 6.
a=- 6.
應(yīng)選B.
例11 兩條直線(xiàn)A1x+B1y+C1=0,A2x+B2y+C2=0垂直的充要條件是 ( )
A.A1A2+B1B2=0 B.A1A2-B1B2=0
C.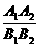 =-1
D.
=-1
D.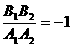
解 若B1B2=0,不妨設(shè)B1=0,則直線(xiàn)l1∶A1x+C1=0,l1是垂直與x軸的直 線(xiàn),由于l1⊥l2,所以l2是垂直y軸的直線(xiàn),從而l2∶B2y+C2=0,即A2=0
故 A1A2+B1B2=0
若B1B2≠0,則l1和l2的方程可化為y=-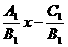 ,y=-
,y=-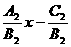 ,得k1=-
,得k1=-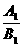 ,k2=-
,k2=-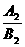 ,
,
由l1⊥l2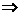 k1·k2=-1
k1·k2=-1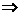
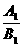 ·
·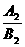 =-1
=-1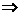 A1A2+B1B2=0.
A1A2+B1B2=0.
綜上有若l1⊥l2,則A1A2+B1B2=0
反之,若A1A2+B1B2=0
1°A1A2≠0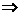 B1B2≠0
B1B2≠0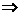 A1A2=-B1B2
A1A2=-B1B2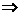
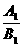 =-
=-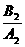
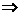
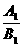 ·
·
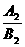 =-1
=-1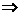 (
(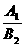 )·(
)·(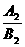 )=-1,
)=-1,
即k1·k2=-1
所以l1⊥l2.
2°若A1·A2=0,不妨設(shè)A1=0,且A2≠0,則B1≠0且B1·B2=0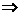 B2=0 ,
B2=0 ,
所以l1∶B1y+C1=0,是垂直y軸的直線(xiàn);
l2∶A2x+C2=0,是垂直x軸的直線(xiàn);
于是l1⊥l2
又若A1=0且A2=0則l1∶B1y+C1=0,l2∶B2y+C2=0,則l1∥l2,此與
l1⊥l2矛盾.
綜上有 若A1A2+B1B2=0,則l1⊥l2
綜合(1)、(2)知,l1⊥l2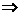 A1A2=B1B2=0
A1A2=B1B2=0
故應(yīng)選A.
例12 如果直線(xiàn)ax+2y+1=0與直線(xiàn)x+y-2=0互相垂直,那么a 的值等于( )
A.1 B.-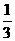 C. -
C. -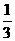 D.-2
D.-2
解:兩直線(xiàn)l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0,互相垂直的充要條件是 :
A1A2+B1B2=0
∴由題設(shè)得a·1+2·1=0,從而a=-2.
應(yīng)選D.
例13 點(diǎn)P(2,5)關(guān)于直線(xiàn)x+y=0的對(duì)稱(chēng)點(diǎn)的坐標(biāo)是( )
A.(5,2) B.(2,-5)
C.(-5,-2) D.(-2,-5)
解:設(shè)P(2,5)和Q(m,n)關(guān)于直線(xiàn)y=-x對(duì)稱(chēng),則PQ中點(diǎn)R(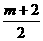 ,
,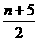 )在y=-x上,且KPQ·(-1)=-1.
)在y=-x上,且KPQ·(-1)=-1.
∴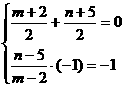 ,解得
,解得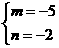
∴對(duì)稱(chēng)點(diǎn)Q的坐標(biāo)是(-5,-2).
應(yīng)選C.
例14 原點(diǎn)關(guān)于直線(xiàn)8x+6y=25的對(duì)稱(chēng)點(diǎn)坐標(biāo)是( )
A.(2,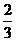 ) B.(
) B.(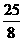 ,
,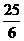 )
)
C.(3,4) D.(4,3)
解:設(shè)(m,n)為所求,則
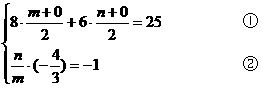
解得m=4,n=3
∴應(yīng)選D.
例15 在直角坐標(biāo)中,△ABC的三個(gè)頂點(diǎn)是:A(0,3),B(3,3),C(2 ,0),若直線(xiàn)x=a,將△ABC分割成面積相等的兩部分,則實(shí)數(shù)a的值是( )
A.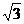 B.1+
B.1+ C.1+
C.1+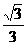 D.2-
D.2-
解 如圖
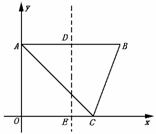
易知直線(xiàn)AC的方程是y=3,直線(xiàn)AC的方程是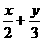 =1,即3x+ 2y=6.
=1,即3x+ 2y=6.
設(shè)直線(xiàn)x=a與AB交于D,與AC交于E,則D,E的坐標(biāo)分別為D(a,3),E(a,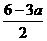 )
)
從而|DE|=3-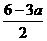 =
=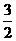 a
a
S△ADE=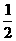 AD·DE=
AD·DE=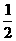 a·
a·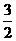 a=
a=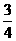 a2
(1)
a2
(1)
又S△ABC=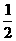 ·3·=
·3·=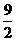 ,
,
S△ADE=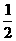 ·S△ACB=
·S△ACB=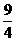 , (2)
, (2)
由(1),(2)有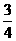 a2=
a2=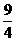 ,解得a=
,解得a=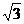
應(yīng)選A.
例16 以A(1,3)、B(-5,1)為端點(diǎn)的線(xiàn)段垂直平分線(xiàn)的方程是( )
A.3x-y+8=0 B.3x+y+4=0
C.2x+y+2=0 D.3x+y+8=0
解:設(shè)P(x,y)為線(xiàn)段AB的中垂線(xiàn)上的點(diǎn),
則│PA│=│PB│
即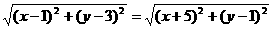 ,化簡(jiǎn)得3x+y+4= 0.
,化簡(jiǎn)得3x+y+4= 0.
應(yīng)選B.
例17 在直角坐標(biāo)系xoy中,過(guò)點(diǎn)P(-3,4)的直線(xiàn)1與直線(xiàn)OP的夾角為45°, 求1的方程.
解:設(shè)1的斜率為k,kOP=-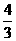 ,
,
∴tg45°=│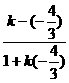 │=│
│=│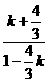 │=│
│=│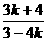 │,
│,
得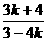 =±1,解出k=-
=±1,解出k=-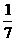 ,7
,7
∴1的方程為y-4=-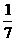 (x+3)或y-4=7(x+3).
(x+3)或y-4=7(x+3).
即1的方程為x+7y-25=0或7x-y+25=0.
例18 點(diǎn)(0,1)到直線(xiàn)x+y=2的距離是 .
解:d=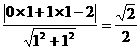

[同步達(dá)綱練習(xí)]
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com