
題目列表(包括答案和解析)
8. 已知
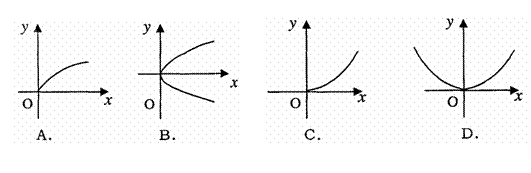
已知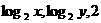 成等差數列,則M(x,y)的軌跡為 ( )
成等差數列,則M(x,y)的軌跡為 ( )
7.設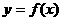 為可導的奇函數,且
為可導的奇函數,且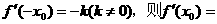 ( )
( )
A.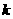 B.
B.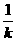 C.-
C.-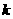 D.-
D.-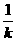
6.已知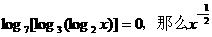 等于 ( )
等于 ( )
A.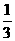 B.
B.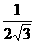 C.
C.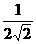 D.
D.
5.圓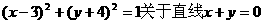 對稱的圓的方程是 ( )
對稱的圓的方程是 ( )
A.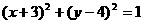 B.
B.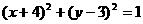
C.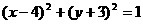 D.
D.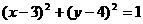
4.將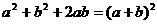 改寫成全稱命題是 ( )
改寫成全稱命題是 ( )
A.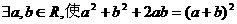
B.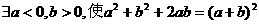
C.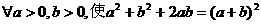
D.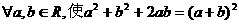
3.問題:①某社區有500個家庭,其中高收入家庭125戶,中等收入家庭280戶,低收入家庭95戶,為了了解購買力的某項指標,要從中抽出一個容量為100戶的樣本;②從10名學生中抽出3人參加座談會。
方法:Ⅰ隨機抽樣法;Ⅱ系統抽樣法;Ⅲ分層抽樣法。
問題與方法配對正確的是 ( )
A.①Ⅲ,②Ⅰ B.①Ⅰ,②Ⅱ C.①Ⅱ,②Ⅲ D.①Ⅲ,②Ⅱ
2.設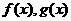 是定義在R上的函數,
是定義在R上的函數,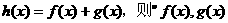 均為偶函數”是“
均為偶函數”是“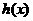 為偶函數”的 ( )
為偶函數”的 ( )
A.充要條件 B.充分不必要條件
C.必要不充分條件 D.既不充分又不必要條件
1.設集合M={-1,0,1},N={a,a2},則使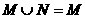 成立的a的值是 ( )
成立的a的值是 ( )
A.-1 B.0 C.1 D.-1或1
22.(1)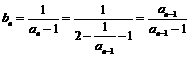 ,而
,而 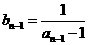 ,
,
∴ 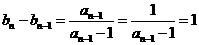 .
.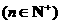
∴ {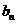 }是首項為
}是首項為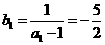 ,公差為1的等差數列.…………… 4分
,公差為1的等差數列.…………… 4分
(2)由(1)有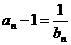 ,而
,而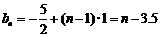 , ∴
, ∴ 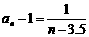 .對于函數
.對于函數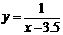 ,在x>3.5時,y>0,
,在x>3.5時,y>0,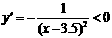 ,在(3.5,
,在(3.5, )上為減函數.
)上為減函數.
故當n=4時,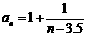 取最大值3. ……………………………… 6分
取最大值3. ……………………………… 6分
而函數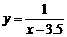 在x<3.5時,y<0,
在x<3.5時,y<0,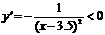 ,在(
,在(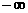 ,3.5)上也為減函數.故當n=3時,取最小值,
,3.5)上也為減函數.故當n=3時,取最小值,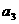 =-1. ……………………………………… 8分
=-1. ……………………………………… 8分
(3)
用數學歸納法證明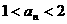 ,再證明
,再證明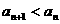
① 當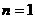 時,
時,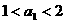 成立; ……………………………………… 9分
成立; ……………………………………… 9分
②假設當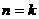 時命題成立,即
時命題成立,即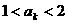 ,
,
當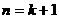 時,
時,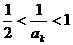
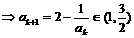
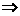
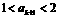
故當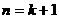 時也成立, ……………………………………… 11分
時也成立, ……………………………………… 11分
綜合①②有,命題對任意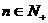 時成立,即
時成立,即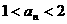 . …………12分
. …………12分
(也可設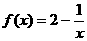 (1≤
(1≤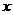 ≤2),則
≤2),則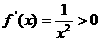 ,
,
故
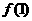
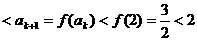 ).
).
下證: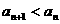
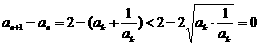
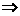
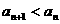 .………………………14分
.………………………14分
(本小題若不用數學歸納法證明,需對應給分。)
21.解(1)∵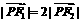 ,
,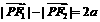 ,∴
,∴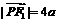 ,
,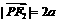 .
.
∵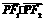 =0,∴(4a)2+(2a)2=(2c)2,∴
=0,∴(4a)2+(2a)2=(2c)2,∴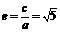 .…………………4分
.…………………4分
(2)由(1)知,雙曲線的方程可設為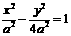 ,漸近線方程為
,漸近線方程為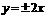 .……5分
.……5分
設P1(x1,2x1),P2(x2,-2x2),P(x,y).………………………………………6分
∵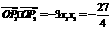 ,∴
,∴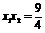 . ∵
. ∵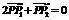 ,∴
,∴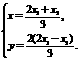 …………10分
…………10分
∵點P在雙曲線上,∴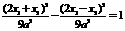 .
.
化簡得,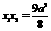 .∴
.∴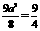 .∴
.∴ 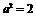 .∴雙曲線的方程為
.∴雙曲線的方程為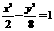 …………12分
…………12分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com