
題目列表(包括答案和解析)
2.雙曲線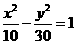 的離心率為
的離心率為
A.2
B.3
C. 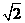 D.
D.
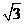
1.設集合A={ |
| } ,B={
} ,B={ |
| },則A∩B=
},則A∩B=
A.(-2,2) B.(-3,2) C.(-3,-2) D.(2,3)
21、已知f(x)在(-1,1)上有定義,f(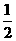 )=-1,且滿足x,y∈(-1,1)有f(x)+f(y)=f(
)=-1,且滿足x,y∈(-1,1)有f(x)+f(y)=f(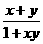 )
)
⑴證明:f(x)在(-1,1)上為奇函數;
⑵對數列x1=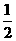 ,xn+1=
,xn+1= ,求f(xn);
,求f(xn);
⑶求證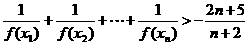
(Ⅰ)證明:令x=y=0,∴2f(0)=f(0),∴f(0)=0
令y=-x,則f(x)+f(-x)=f(0)=0
∴f(x)+f(-x)=0 ∴f(-x)=-f(x)
∴f(x)為奇函數 4分
(Ⅱ)解:f(x1)=f(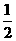 )=-1,f(xn+1)=f(
)=-1,f(xn+1)=f( )=f(
)=f(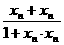 )=f(xn)+f(xn)=2f(xn)
)=f(xn)+f(xn)=2f(xn)
∴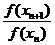 =2即{f(xn)}是以-1為首項,2為公比的等比數列
=2即{f(xn)}是以-1為首項,2為公比的等比數列
∴f(xn)=-2n-1
(Ⅲ)解: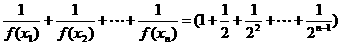

而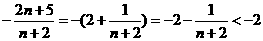
∴
20、(本小題滿分12分)
已知函數 ,且函數
,且函數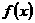 與
與 的圖像關于直線
的圖像關于直線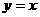 對稱,又
對稱,又 ,
,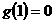 .
.
(Ⅰ) 求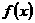 的值域;
的值域;
(Ⅱ) 是否存在實數m,使得命題  和
和 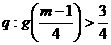 滿足復合命題
滿足復合命題 
 為真命題?若存在,求出m的取值范圍;若不存在,說明理由.
為真命題?若存在,求出m的取值范圍;若不存在,說明理由.
解:(Ⅰ)依題意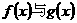 互為反函數,由
互為反函數,由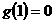 得
得
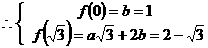 ,得
,得 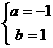
 ……………………3分
……………………3分
故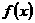 在
在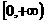 上是減函數
上是減函數
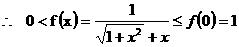
即 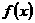 的值域為
的值域為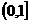 . ……………………6分
. ……………………6分
(Ⅱ)由(Ⅰ)知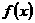 是
是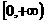 上的減函數,
上的減函數, 是
是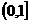 上的減函數,
上的減函數,
又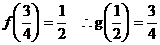
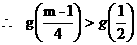 ……………………9分
……………………9分
故 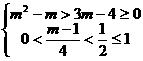 解得
解得 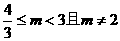
因此,存在實數m,使得命題 
 為真命題,且m的取值范圍為
為真命題,且m的取值范圍為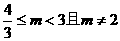 . ……………………12分
. ……………………12分
19、(本小題滿分14分)
已知函數 ,
,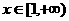
①當 時,求函數
時,求函數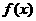 的最小值。
的最小值。
②若對任意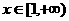 ,
,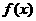 >
> 恒成立,試求實數
恒成立,試求實數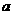 的取值范圍。
的取值范圍。
(1)當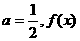 有最小值為
有最小值為 。…….7分
。…….7分
(2)當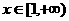 ,使函數
,使函數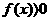 恒成立時,故
恒成立時,故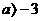 。。。。14分
。。。。14分
18、本小題滿分13分)
某單位用2160萬元購得一塊空地,計劃在該地塊上建造一棟至少10層、每層2000平方米的樓房.經測算,如果將樓房建為x(x≥10)層,則每平方米的平均建筑費用為560+48x(單位:元).為了使樓房每平方米的平均綜合費用最少,該樓房應建為多少層?
(注:平均綜合費用=平均建筑費用+平均購地費用,平均購地費用= )
)
[解析]設樓房每平方米的平均綜合費為f(x)元,則
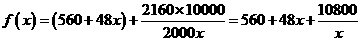

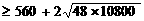 = 560+2
= 560+2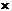 720=200
720=200
當且僅當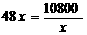 , 即
, 即 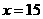 時取等號,
時取等號, ,
,
所以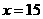 滿足條件
滿足條件
因此 當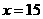 時,f(x)取最小值
時,f(x)取最小值 ;
;
答:為了樓房每平方米的平均綜合費最少,該樓房應建為15層
17、已知f(x)=2x-1的反函數為 (x),g(x)=log4(3x+1).
(x),g(x)=log4(3x+1).
⑴若f-1(x)≤g(x),求x的取值范圍D;
⑵設函數H(x)=g(x)- (x),當x∈D時,求函數H(x)的值域.
(x),當x∈D時,求函數H(x)的值域.
解:(Ⅰ)∵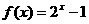
∴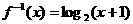 (x>-1)
(x>-1)
由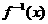 ≤g(x) ∴
≤g(x) ∴
解得0≤x≤1 ∴D=[0,1]
(Ⅱ)H(x)=g(x)-
∵0≤x≤1 ∴1≤3-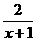 ≤2
≤2
∴0≤H(x)≤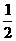 ∴H(x)的值域為[0,
∴H(x)的值域為[0,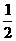 ]
]
16、(本小題滿分12分) 解不等式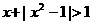
解:①當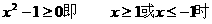
原式變形為 …………4分
…………4分
∴x<-2或x>1 ………………6分
②當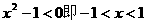 時
時
原式變形為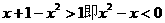 …………8分
…………8分
∴0<x<1 …………10分
綜上知:原不等式解集為 …………12分
…………12分
15、關于函數 有下列命題:
有下列命題:
①函數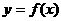 的圖象關于
的圖象關于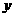 軸對稱;
軸對稱;
②在區間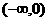 上,函數
上,函數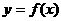 是減函數;
是減函數;
③函數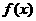 的最小值為
的最小值為 ;
;
④在區間 上,函數
上,函數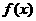 是增函數.
是增函數.
其中正確命題序號為_______________.(1) (3) (4)
14、13.函數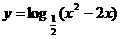 的單調遞減區間是________________________.(2,+∞)
的單調遞減區間是________________________.(2,+∞)
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com