
題目列表(包括答案和解析)
19. (本小題滿分12分)
(1) 由條件得:a +2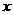 b
=–
b
=–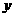 a +
a + 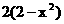 b,
b,
∴ 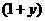 a +
a +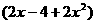 b = 0 ,
b = 0 ,
∵向量 a與b 不共線, ∴ 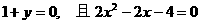 ,
,
解得 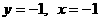 或
或 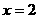 .
.
(2) ∵ a·b = cos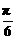 sin
sin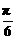 + sin(–
+ sin(–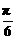 )cos
)cos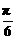 = 0, ∴a⊥b .
= 0, ∴a⊥b .
又∵c⊥d , ∴c·d = 0.
∵由條件知: |a | = 1, | b | = 1, a·b = 0,
∴ c·d = (a +2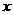 b)·[–
b)·[–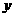 a +
a + 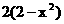 b]
b]
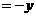 a 2
a 2 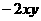 a·b+
a·b+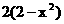 a·b
a·b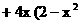 )b 2
)b 2 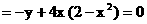 .
.
∴ 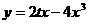 , 即
, 即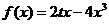 .
.
18. (本小題滿分12分)
(1)∵ 這輛汽車在第一、二個交通崗均未遇到紅燈,而第三個交通崗遇到紅燈
∴ 概率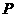 = (1 –
= (1 –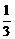 )(1 –
)(1 –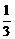 )
)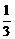 =
= 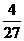 ;
;
(2)(理)∵
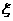 ∽
∽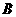 ( 8,
( 8, 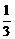 ),
),
∴ 期望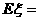 8´
8´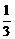 =
=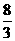 , 方差
, 方差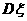 = 8´
= 8´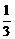 ´( 1 –
´( 1 –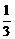 ) =
) = 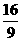 .
.
(文)概率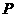 =
= 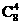 ´(
´(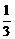 )4´ (1–
)4´ (1–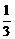 )2 =
)2 = 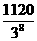 .
. 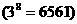
17. (本小題滿分12分)
∵ 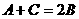 ,∴
,∴ 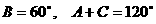 .
.
由 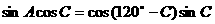 , 得
, 得
即 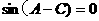
又 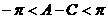 , ∴
, ∴ 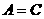 , △
, △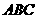 為等邊三角形.
為等邊三角形.
13.  /真 14.
/真 14. 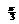 15. 0.99 16. 126, 24789
15. 0.99 16. 126, 24789
23. (附加題, 本題滿分6分, 但全卷總分不超過150分)
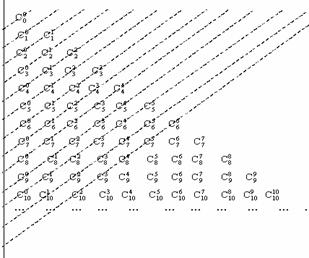
把“楊輝三角形”向左對齊如圖所示,
分別按圖中虛線,由上至下把劃到的數(shù)相加,
寫在虛線左下端點(左邊豎線的左側(cè))處,
把這些和由上至下排列得一個數(shù)列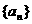 .
.
(1) 觀察數(shù)列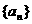 ,寫出一個你能發(fā)
,寫出一個你能發(fā)
現(xiàn)的遞推公式(不必證明);
(2) 設(shè)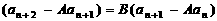 ,
,
求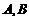 的值, 并求
的值, 并求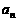 .
.
高考科目教學(xué)質(zhì)量第一次檢測
數(shù)學(xué)參考評分標(biāo)準(zhǔn) (文理合卷)
22. (本小題滿分14分)
定義在定義域D內(nèi)的函數(shù)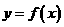 ,若對任意的
,若對任意的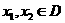 都有
都有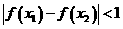 ,則稱函數(shù)
,則稱函數(shù)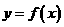 為“西湖函數(shù)”,否則稱“非西湖函數(shù)”.函數(shù)
為“西湖函數(shù)”,否則稱“非西湖函數(shù)”.函數(shù)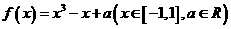 是否為“西湖函數(shù)”?如果是,請給出證明;如果不是,請說明理由.
是否為“西湖函數(shù)”?如果是,請給出證明;如果不是,請說明理由.
21. (本小題滿分12分)
已知數(shù)列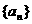 ,其中
,其中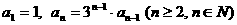 , 數(shù)列
, 數(shù)列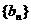 的前
的前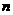 項的和
項的和
 .
.
(1) 求數(shù)列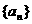 的通項公式;
的通項公式;
(2) 求數(shù)列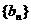 的通項公式;
的通項公式;
(3) (理科做文科不做) 求數(shù)列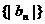 的前n項和
的前n項和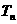 .
.
20. (本小題滿分12分)
已知一物體做圓周運動, 出發(fā)后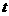 分鐘內(nèi)走過的路程
分鐘內(nèi)走過的路程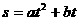 , 最初用5分鐘走完第一圈, 接下去用3分鐘走完第二圈.
, 最初用5分鐘走完第一圈, 接下去用3分鐘走完第二圈.
(1) 試問該物體走完第三圈用了多長時間? (結(jié)果可用無理數(shù)表示)
(2) (理科做文科不做) 試問從第幾圈開始, 走完一圈的時間不超過1分鐘?
19. (本小題滿分12分)
已知平面向量 a與b 不共線,若存在非零實數(shù)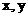 , 使得 c = a +2
, 使得 c = a +2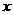 b ,
b ,
d =–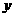 a +
a + 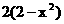 b .
b .
(1) 當(dāng)c= d時,求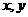 的值;
的值;
(2) 若a = (cos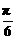 , sin(–
, sin(–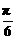 )), b = (sin
)), b = (sin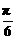 , cos
, cos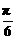 ),且c⊥d , 試求函數(shù)
),且c⊥d , 試求函數(shù)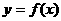 的表達式.
的表達式.
18. (本小題滿分12分)
從汽車東站駕車至汽車西站的途中要經(jīng)過8個交通崗,假設(shè)某輛汽車在各交通崗遇到紅燈的事件是獨立的,并且概率都是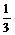 .
.
(1)求這輛汽車首次遇到紅燈前,已經(jīng)過了兩個交通崗的概率;
(2)(理)這輛汽車在途中遇到紅燈數(shù)ξ的期望與方差.
(文)這輛汽車在途中恰好遇到4次紅燈的概率.
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com