
題目列表(包括答案和解析)
19. (本小題14分)
(本小題14分)
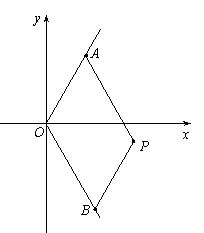
如圖,
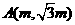 和
和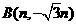 兩點分別在射線OS、OT上移動,且
兩點分別在射線OS、OT上移動,且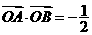 ,O為坐標原點,動點P滿足
,O為坐標原點,動點P滿足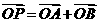 .
.
(Ⅰ)求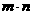 的值;
的值;
(Ⅱ)求P點的軌跡C的方程,并說明它表示怎樣
的曲線?
(Ⅲ)若直線l過點E(2,0)交(Ⅱ)中曲線C于M、N兩
點,且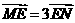 ,求l的方程.
,求l的方程.
解:(Ⅰ)由已知得
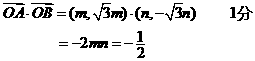
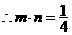 …………4分
…………4分
(Ⅱ)設P點坐標為(x,y)(x>0),由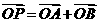 得
得
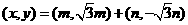
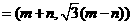 …………5分
…………5分
∴ 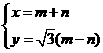 消去m,n可得
消去m,n可得
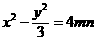 ,又因
,又因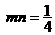 8分
8分
∴ P點的軌跡方程為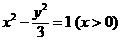
它表示以坐標原點為中心,焦點在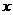 軸上,且實軸長為2,焦距為4的雙曲線
軸上,且實軸長為2,焦距為4的雙曲線
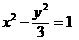 的右支
…………9分
的右支
…………9分
(Ⅲ)設直線l的方程為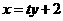 ,將其代入C的方程得
,將其代入C的方程得

即 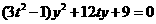
易知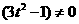 (否則,直線l的斜率為
(否則,直線l的斜率為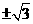 ,它與漸近線平行,不符合題意)
,它與漸近線平行,不符合題意)
又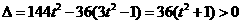
設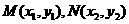 ,則
,則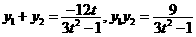
∵ l與C的兩個交點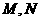 在
在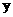 軸的右側
軸的右側
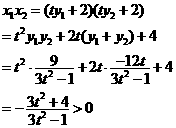
∴ 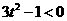 ,即
,即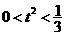
又由 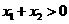 同理可得
同理可得 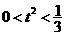 …………11分
…………11分
由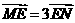 得
得
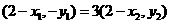
∴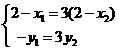
由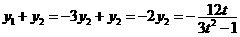 得
得
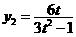
由 得
得

消去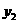 得
得 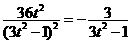
解之得: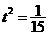 ,滿足
,滿足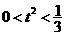 …………13分
…………13分
故所求直線l存在,其方程為: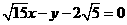 或
或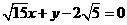 …………14分
…………14分
18.(本小題13分)
已知: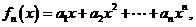
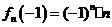 ,
,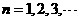 .
.
(I)求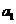 、
、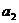 、
、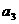 ;
;
(II)求數列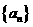 的通項公式;
的通項公式;
(II)求證: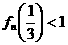
解:(I)由已知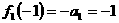 ,所以
,所以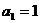 1分
1分
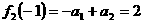 ,所以
,所以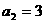
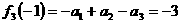 ,所以
,所以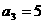 3分
3分
(II)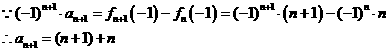
即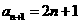
所以對于任意的 ,
, 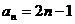 7分
7分
(III)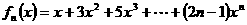
∴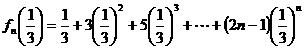 ①
①
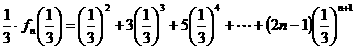 ②
②
①─②,得
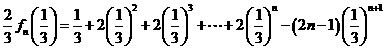 9分
9分
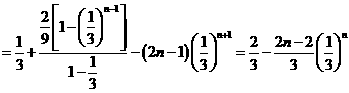
∴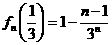 ,
12分
,
12分
又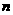 =1,2,3…,故
=1,2,3…,故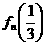 < 1
13分
< 1
13分
17. (本小題13分)
(本小題13分)
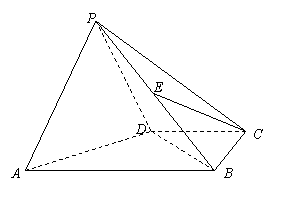
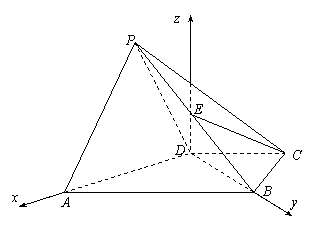
如圖,在四棱錐P-ABCD中,平面PAD⊥平面ABCD,  ,
,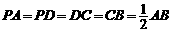 ,E是BD的中點.
,E是BD的中點.
(Ⅰ)求證:EC//平面APD;
(Ⅱ)求BP與平面ABCD所成角的正切值;
(Ⅲ) 求二面角P-AB-D的大小.
解法一:(Ⅰ)如圖,取PA中點F,連結EF、FD,
∵E是BP的中點,
∵EF//AB且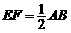 ,
,
又∵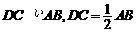
∴EF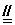 DC∴四邊形EFDC是平行四邊形,故得EC//FD
…………2分
DC∴四邊形EFDC是平行四邊形,故得EC//FD
…………2分
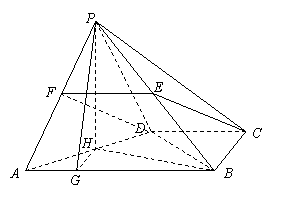
又∵EC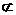 平面PAD,FD
平面PAD,FD 平面PAD
平面PAD
∴EC//平面ADE …………4分
(Ⅱ)取AD中點H,連結PH,因為PA=PD,所以PH⊥AD
∵平面PAD⊥平面ABCD于AD
∴PH⊥面ABCD
∴HB是PB在平面ABCD內的射影
∴∠PBH是PB與平面ABCD所成角 …………6分
∵四邊形ABCD中,
 ∴四邊形ABCD是直角梯形
∴四邊形ABCD是直角梯形
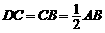
設AB=2a,則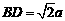 ,
,
在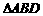 中,易得
中,易得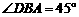 ,
,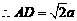
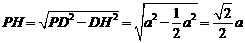 ,
,
又∵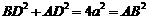 ,
,
∴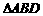 是等腰直角三角形,
是等腰直角三角形,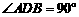
∴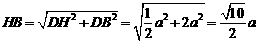
∴在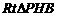 中,
中,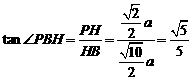 …………10分
…………10分
(Ⅲ)在平面ABCD內過點H作AB的垂線交AB于G點,連結PG,則HG是PG在平面ABCD上的射影,故PG⊥AB,所以∠PGH是二面角P-AB-D的平面角,由AB=2a …………11分
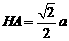 ,又
,又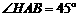 ∴
∴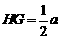
在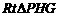 中,
中,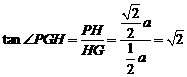 13分
13分
∴二面角P-AB-D的大小為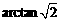 …………14分
…………14分
解法二:(Ⅰ)同解法一 4分
(Ⅱ)設AB=2a,同解法一中的(Ⅱ)可得
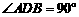
如圖,以D點為原點,DA所在直線為x軸,DB所在直線為y軸,過D點且垂直于平面ABCD的直線為z軸建立空間直角坐標系. …………5分
 則
則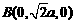 ,
,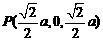 ,則
,則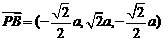 ,平面ABCD的一個法向量為m=(0,0,1), …………7分
,平面ABCD的一個法向量為m=(0,0,1), …………7分
所以,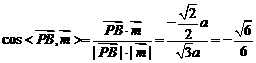
可得PB與平面ABCD所成角的正弦值為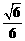
所以 PB與平面ABCD所成角的正切值為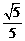 …………10分
…………10分
(Ⅲ)易知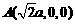 ,則
,則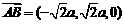 ,設平面PAB的一個法向量為
,設平面PAB的一個法向量為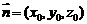 ,則
,則
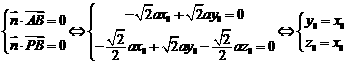 ,令
,令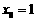 ,可得
,可得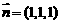 ……12分
……12分
得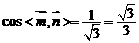 ,
,
所以二面角P-AB-D的大小為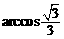 …………14分
…………14分
16.(本小題13分)
某公司有10萬元資金用于投資,如果投資甲項目,根據市場分析知道:一年后可能獲利10﹪,可能損失10﹪,可能不賠不賺,這三種情況發生的概率分別為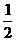 ,
,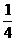 ,
,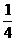 ;如果投資乙項目,一年后可能獲利20﹪,也可能損失20﹪,這兩種情況發生的概率分別為
;如果投資乙項目,一年后可能獲利20﹪,也可能損失20﹪,這兩種情況發生的概率分別為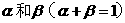 .
.
(Ⅰ)如果把10萬元投資甲項目,用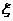 表示投資收益(收益=回收資金-投資資金),
表示投資收益(收益=回收資金-投資資金),
求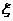 的概率分布及
的概率分布及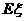 ;
;
(Ⅱ)若把10萬元投資投資乙項目的平均收益不低于投資甲項目的平均收益,求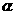 的取值范圍.
的取值范圍.
解:(Ⅰ)依題意,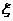 的可能取值為1,0,-1
…………1分
的可能取值為1,0,-1
…………1分
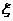 的分布列為
的分布列為
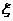 |
1 |
0 |
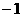 |
|
p |
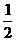 |
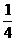 |
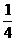 |
…………4分
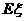 =
=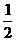
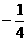 =
=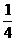 …………6分
…………6分
(Ⅱ)設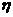 表示10萬元投資乙項目的收益,則
表示10萬元投資乙項目的收益,則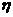 的分布列為
的分布列為
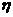 |
2 |
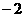 |
|
p |
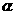 |
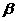 |
…………8分
 …………10分
…………10分
依題意要求
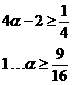 …………13分
…………13分
注:只寫出 扣1分
扣1分
15.(本小題12分)
已知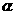 為鈍角,且
為鈍角,且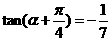
求: (Ⅰ)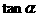 ;
;
(Ⅱ)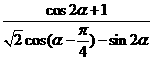 .
.
解: (Ⅰ)由已知: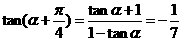 …………………2分
…………………2分
得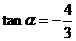 …………………5分
…………………5分
(Ⅱ)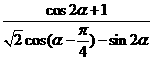
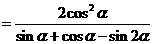
 …………………8分
…………………8分
∵ 且
且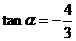
∴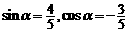 …………………10分
…………………10分
∴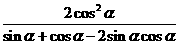
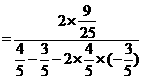
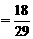 …………………12分
…………………12分
14.數列{ a },{ b
},{ b }(
}(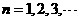 )由下列條件所確定:
)由下列條件所確定:
(ⅰ)a1<0, b1>0 ;
(ⅱ)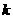 ≥2時,ak與bk滿足如下條件:
≥2時,ak與bk滿足如下條件:
當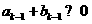 時,ak= ak-1,
bk=
時,ak= ak-1,
bk=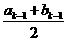 ;
;
當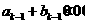 時,ak=
時,ak= 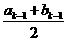 , bk=b k-1.
, bk=b k-1.
那么,當a1=-5,b1=5時, { a }的通項公式為
}的通項公式為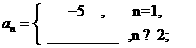
當b1> b2>…>bn(n≥2)時,用a1,b1表示{ bk }的通項公式為bk= (k=2,3…,n).
(1)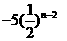 ;(2)
;(2)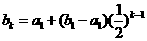
13.有這樣一種數學游戲:在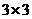 的表格中,要求每個格子中都填上1、2、3三個數字中的某一個數字,且每一行和每一列都不能出現重復的數字,則此游戲共有 12 種不同的填法
的表格中,要求每個格子中都填上1、2、3三個數字中的某一個數字,且每一行和每一列都不能出現重復的數字,則此游戲共有 12 種不同的填法
12.已知函數 ,若
,若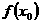 ≥2,則
≥2,則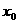 的取值范圍是
的取值范圍是
11.已知向量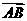 =(4, 0),
=(4, 0),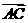 =(2, 2),則
=(2, 2),則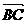 = (-2,2) ;
= (-2,2) ;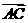 與
與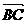 的夾角的大小為 90°
的夾角的大小為 90°
10.一個與球心距離為2的平面截球所得的圓面面積為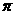 ,則球的表面積為 20
,則球的表面積為 20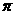
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com