
題目列表(包括答案和解析)
6. 如圖,將網格中的三條線段沿網格線上下或左右平移,組成一個首尾相連的三角形,則三條線段一共至少需要移動D
如圖,將網格中的三條線段沿網格線上下或左右平移,組成一個首尾相連的三角形,則三條線段一共至少需要移動D
A.12格 B.11格 C.10格 D.9格
5.對于任意的兩個數對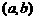 和
和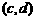 ,定義運算
,定義運算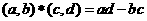 ,若
,若 ,則復數
,則復數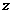 為
為
A.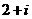 B.
B. 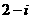 C.
C.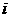 D.
D.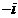
4.某個容器的底部為圓柱,頂部為圓錐,其正視圖如圖,
則這個容器的表面積為
A.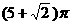
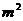 B.
B.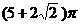
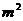
C.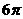
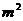 D.
D.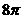
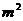
3.等差數列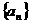 中,如果
中,如果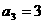 ,
,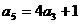 ,那么
,那么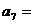
A.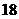 B.
B. C.
C. D.
D.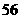

2.下列函數中,在其定義域內既是奇函數又是減函數的是
A.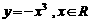 B.
B.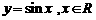
C.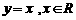 D.
D. 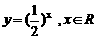
1.特稱命題“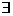 實數x,使
實數x,使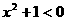 ”的否定可以寫成
”的否定可以寫成
A.若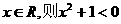 B.
B.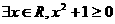
C.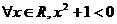 D.
D.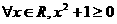
13. 已知數列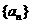 的前
的前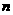 項和
項和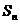 滿足:
滿足: ,
,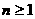 .
.
⑴寫出求數列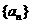 的前3項
的前3項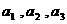 ;
;
⑵求數列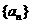 的通項公式;
的通項公式;
⑶證明:對任意的整數m>4,有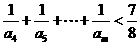 .
.
12. 將等差數列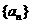 的項按如下次序和規則分組,第一組為
的項按如下次序和規則分組,第一組為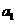 ,第二組為
,第二組為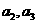 ,第三組為
,第三組為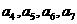 ,第四組
,第四組 ,第
,第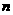 組共有
組共有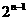 項組成,并把第
項組成,并把第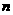 組的各項之和記作
組的各項之和記作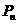
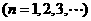 ,已知
,已知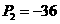 ,
,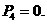
(1)求數列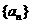 的通項公式;
的通項公式;
(2)若以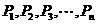 為項構成數列
為項構成數列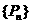 ,試求
,試求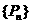 的前8項之和
的前8項之和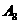 (寫出具體數值).
(寫出具體數值).
11. 設數列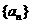 .
.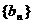 滿足:
滿足: ,且數列
,且數列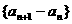
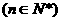 是等差數列,{bn-2}是等比數列.
是等差數列,{bn-2}是等比數列.
(Ⅰ)求數列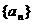 ,
,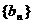 的通項公式;
的通項公式;
(Ⅱ)是否存在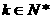 ,使
,使 .若存在,求出k;若不存在,說明理由.
.若存在,求出k;若不存在,說明理由.
10. 已知數列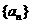 的前
的前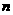 項和為
項和為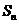 ,設
,設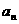 是
是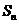 與2的等差中項,數列
與2的等差中項,數列 中,
中,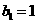 ,點
,點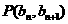 在直線
在直線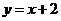 上.
上.
(1)求數列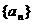 ,
,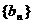 的通項公式
的通項公式
(2)若數列 的前
的前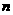 項和為
項和為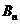 ,比較
,比較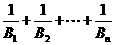 與2的大小;
與2的大小;
(3)令 ,是否存在正整數
,是否存在正整數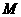 ,使得
,使得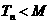 對一切正整數
對一切正整數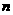 都成立?若存在,求出
都成立?若存在,求出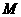 的最小值;若不存在,請說明理由.
的最小值;若不存在,請說明理由.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com