精品一区二区免费在线观看_国产精品久久久久久av福利软件_97成人精品区在线播放_国内成人精品一区

19．(本小題滿分12分)

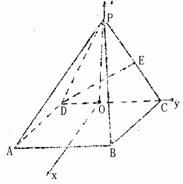
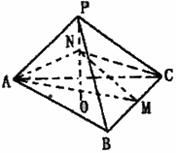
　　　 如圖，四棱錐P-ABCD中，底面四邊形ABCD是正方形，側(cè)面PDC是邊長(zhǎng)為a的正

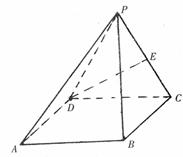　 三角形，且平面PDC⊥底面ABCD，E為PC的中點(diǎn)。

　　　 (I)求異面直線PA與DE所成的角；

　　　 (II)求點(diǎn)D到面PAB的距離.

(1)解法一：連結(jié)AC，BD交于點(diǎn)O，連結(jié)EO.

∵四邊形ABCD為正方形，∴AO=CO，又∵PE=EC，∴PA∥EO，

∴∠DEO為異面直線PA與DE所成的角……………………3分

∵面PCD⊥面ABCD，AD⊥CD，∴AD⊥面PCD，∴AD⊥PD.

在Rt△PAD中，PD=AD=a，則，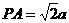

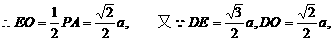
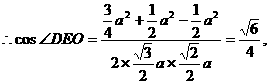
∴異面直線PA與DE的夾角為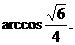……………………6分

(2)取DC的中點(diǎn)M，AB的中點(diǎn)N，連PM、MN、PN.

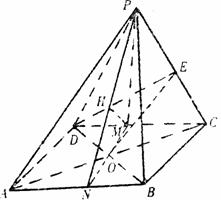
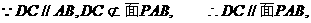
∴D到面PAB的距離等于點(diǎn)M到

面PAB的距離.……7分

過(guò)M作MH⊥PN于H，

∵面PDC⊥面ABCD，PM⊥DC，

∴PM⊥面ABCD，∴PM⊥AB，

又∵AB⊥MN，PM∩MN=M，

∴AB⊥面PMN. ∴面PAB⊥面PMN，

∴MH⊥面PAB，

則MH就是點(diǎn)D到面PAB的距離.……10分

在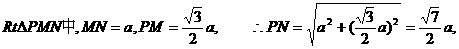

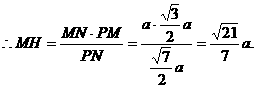　 ………………12分

解法二：如圖取DC的中點(diǎn)O，連PO，

∵△PDC為正三角形，∴PO⊥DC.

又∵面PDC⊥面ABCD，∴PO⊥面ABCD.

如圖建立空間直角坐標(biāo)系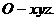

則

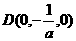.………………………………3分

(1)E為PC中點(diǎn)，　 ，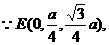

，

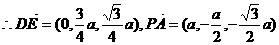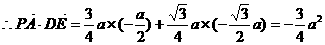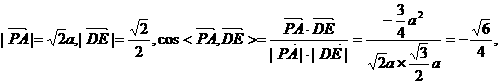
∴異面直線PA與DE所成的角為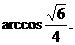……………………6分

(2)可求，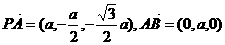

設(shè)面PAB的一個(gè)法向量為，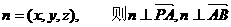

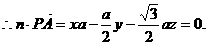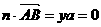　 ①　　 . ②

由②得y=0，代入①得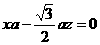

令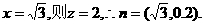…………………………9分

則D到面PAB的距離d等于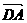在n上射影的絕對(duì)值

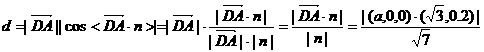
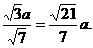
即點(diǎn)D到面PAB的距離等于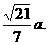………………………………12分

18．(本小題滿分12分)

　　 如圖，A、B兩點(diǎn)之間有6條網(wǎng)線并聯(lián)，它們能通過(guò)的最大信息量分別為1，1，2，2，3，4.現(xiàn)從中任取三條網(wǎng)線且使每條網(wǎng)線通過(guò)最大的信息量.

　 (I)設(shè)選取的三條網(wǎng)線由A到B可通過(guò)的信息總量為x，當(dāng)x≥6時(shí)，則保證信息暢通.求線路信息暢通的概率；

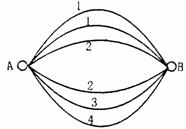　 　 (II)求選取的三條網(wǎng)線可通過(guò)信息總量的數(shù)學(xué)期望.

解：

(I)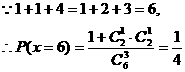

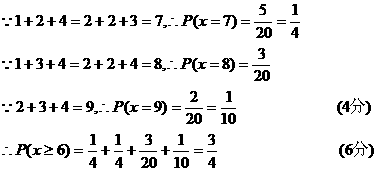
　 (II)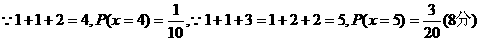

　　　　 ∴線路通過(guò)信息量的數(shù)學(xué)期望

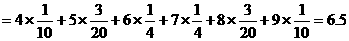　　　　 　　　　　　(11分)

答：(I)線路信息暢通的概率是.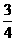

　 (II)線路通過(guò)信息量的數(shù)學(xué)期望是6.5.(12分)

17．(本小題滿分12分)

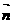　　 已知向量向量與向量夾角為，且.

　 (1)求向量；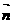

　 (2)若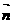向量與向量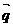=(1，0)的夾角為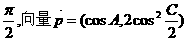，其中A，C

　　　　　　　 為△ABC的內(nèi)角，且A，B，C依次成等差數(shù)列，試求求|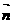+|的取值范圍.

解：(1)設(shè)，有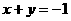　 ① ………………1分

由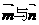夾角為，有.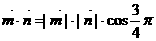

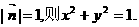∴②………………3分

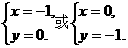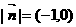由①②解得　 ∴即或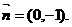…………4分

　 (2)由垂直知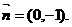…………5分

由2B=A+C　 知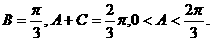……6分

16． 若直線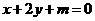按向量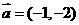平移后與圓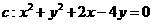相切，則實(shí)數(shù)的值為-13或-3 　　

15．國(guó)家規(guī)定個(gè)人稿費(fèi)納稅辦法是：不超過(guò)800元的不納稅；超過(guò)800 元而不超過(guò)4000元的按超過(guò)800元部分的14%納稅；超過(guò)4000元的按全部稿酬的11%納稅.已知某人出版一本書，共納稅420元時(shí)，這個(gè)人應(yīng)得稿費(fèi)(扣稅前)為3800元.

　 13．甲、乙、丙三人值日，從周一至周六，每人值班兩天，若甲不值周一，乙不值周六，則可排出的不同值日表有

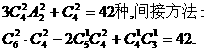種.

14．如右圖，它滿足：(1)第n行首尾兩數(shù)均為n，

(2)表中的遞推關(guān)系類似楊輝三角，則第n行

(n≥2)第2個(gè)數(shù)是

12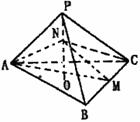．三棱錐P-ABC的高PO=8，AC=BC=3，∠ACB=30°，

M，N分別在BC和PO上，且CM=x，PN=2CM，試問(wèn)

下面的四個(gè)圖象中哪個(gè)圖象大致描繪了三棱錐N-AMC

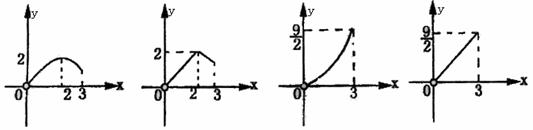　 的體積V與x的變化關(guān)系(如圖)(A)

第Ⅱ卷(非選擇題，共90分)

11．對(duì)某種產(chǎn)品的6件不同正品和4件不同次品，一一進(jìn)行測(cè)試，到區(qū)分出所有次品為止。

　 若所有次品恰好在第五次測(cè)試被全部發(fā)現(xiàn)，則這樣的測(cè)試方法有　　　　　　　　　　 (C)

　　　 A．24種　　　　　　　　　 B．96種　　　　　　　　　

　　　 C．576種　　　　　　　　 D．720種

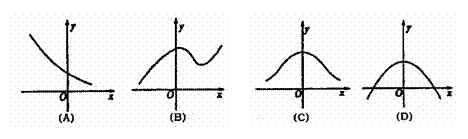
9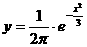．的部分圖象大致是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (C)

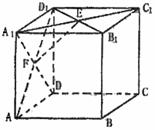　 10．正方體ABCD-A₁B₁C₁D₁，E，F(xiàn)分別是正方形A₁B₁C₁D₁和

　 ADD₁A₁的中心，則EF和CD所成的角是　　　 (B )

　　　 A．60°　　　　　　　　　 B．45°

　　　 C．30°　　　　　　　　　 D．90°

8. 由等式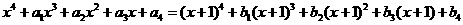

定義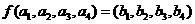，則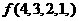等于　　　　　　　　 (D)

　　 A．(1，2，3，4，) 　　　　　　　　　 B．(0，3，4，0，)

　　 C．(-1，0，2，-2) 　　　　　　　　 D．(0，-3，4，-1)．