
⑴設(shè)a=(x1,y1),b=(x2,y2),則:① a∥b(b≠0)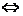 a=
a=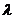 b (
b (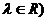
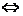 x1y2-x2y1=0;
x1y2-x2y1=0;
② a⊥b(a、b≠0)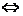 a·b=0
a·b=0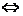 x1x2+y1y2=0 .
x1x2+y1y2=0 .
⑵a·b=|a||b|cos<a,b>=x2+y1y2; 注:①|(zhì)a|cos<a,b>叫做a在b方向上的投影;|b|cos<a,b>叫做b在a方向上的投影;②a·b的幾何意義:a·b等于|a|與|b|在a方向上的投影|b|cos<a,b>的乘積。⑶cos<a,b>=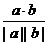 ;
;
⑷三點(diǎn)共線的充要條件P,A,B三點(diǎn)共線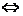
 ;
;
附:(理科)P,A,B,C四點(diǎn)共面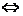
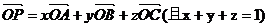 。
。
4.求軌跡的常用方法:
(1)定義法:利用圓錐曲線的定義; (2)直接法(列等式);(3)代入法(相關(guān)點(diǎn)法或轉(zhuǎn)移法);⑷待定系數(shù)法;(5)參數(shù)法;(6)交軌法。
3.直線與圓錐曲線問(wèn)題解法:
⑴直接法(通法):聯(lián)立直線與圓錐曲線方程,構(gòu)造一元二次方程求解。
注意以下問(wèn)題:①聯(lián)立的關(guān)于“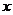 ”還是關(guān)于“
”還是關(guān)于“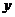 ”的一元二次方程?
”的一元二次方程?
②直線斜率不存在時(shí)考慮了嗎?③判別式驗(yàn)證了嗎?
⑵設(shè)而不求(代點(diǎn)相減法):--------處理弦中點(diǎn)問(wèn)題
步驟如下:①設(shè)點(diǎn)A(x1,y1)、B(x2,y2);②作差得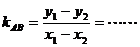 ;③解決問(wèn)題。
;③解決問(wèn)題。
2.結(jié)論 ⑴焦半徑:①橢圓: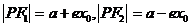 (e為離心率); (左“+”右“-”);②拋物線:
(e為離心率); (左“+”右“-”);②拋物線: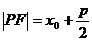
⑵弦長(zhǎng)公式: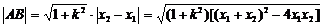
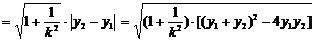 ;
;
注:(Ⅰ)焦點(diǎn)弦長(zhǎng):①橢圓: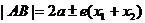 ;②拋物線:
;②拋物線: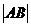 =x1+x2+p=
=x1+x2+p=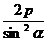 ;(Ⅱ)通徑(最短弦):①橢圓、雙曲線:
;(Ⅱ)通徑(最短弦):①橢圓、雙曲線: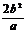 ;②拋物線:2p。
;②拋物線:2p。
⑶過(guò)兩點(diǎn)的橢圓、雙曲線標(biāo)準(zhǔn)方程可設(shè)為: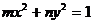 (
(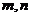 同時(shí)大于0時(shí)表示橢圓,
同時(shí)大于0時(shí)表示橢圓,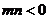 時(shí)表示雙曲線);
時(shí)表示雙曲線);
⑷橢圓中的結(jié)論:①內(nèi)接矩形最大面積 :2ab;
②P,Q為橢圓上任意兩點(diǎn),且OP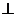 0Q,則
0Q,則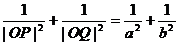 ;
;
③橢圓焦點(diǎn)三角形:<Ⅰ>.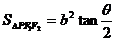 ,(
,(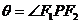 );<Ⅱ>.點(diǎn)
);<Ⅱ>.點(diǎn)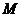 是
是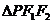 內(nèi)心,
內(nèi)心,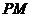 交
交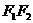 于點(diǎn)
于點(diǎn)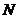 ,則
,則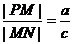 ;
;
④當(dāng)點(diǎn)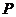 與橢圓短軸頂點(diǎn)重合時(shí)
與橢圓短軸頂點(diǎn)重合時(shí)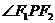 最大;
最大;
⑸雙曲線中的結(jié)論:
①雙曲線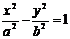 (a>0,b>0)的漸近線:
(a>0,b>0)的漸近線: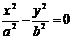 ;
;
②共漸進(jìn)線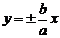 的雙曲線標(biāo)準(zhǔn)方程為
的雙曲線標(biāo)準(zhǔn)方程為 為參數(shù),
為參數(shù),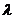 ≠0);
≠0);
③雙曲線焦點(diǎn)三角形:<Ⅰ>.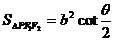 ,(
,(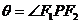 );<Ⅱ>.P是雙曲線
);<Ⅱ>.P是雙曲線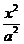 -
- =1(a>0,b>0)的左(右)支上一點(diǎn),F1、F2分別為左、右焦點(diǎn),則△PF1F2的內(nèi)切圓的圓心橫坐標(biāo)為
=1(a>0,b>0)的左(右)支上一點(diǎn),F1、F2分別為左、右焦點(diǎn),則△PF1F2的內(nèi)切圓的圓心橫坐標(biāo)為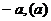 ;
;
④雙曲線為等軸雙曲線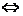
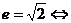 漸近線為
漸近線為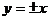
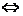 漸近線互相垂直;
漸近線互相垂直;
(6)拋物線中的結(jié)論:
①拋物線y2=2px(p>0)的焦點(diǎn)弦AB性質(zhì):<Ⅰ>.
x1x2=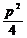 ;y1y2=-p2;
;y1y2=-p2;
<Ⅱ>.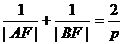 ;<Ⅲ>.以AB為直徑的圓與準(zhǔn)線相切;<Ⅳ>.以AF(或BF)為直徑的圓與
;<Ⅲ>.以AB為直徑的圓與準(zhǔn)線相切;<Ⅳ>.以AF(或BF)為直徑的圓與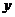 軸相切;<Ⅴ>.
軸相切;<Ⅴ>.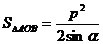 。
。
②拋物線y2=2px(p>0)內(nèi)結(jié)直角三角形OAB的性質(zhì):
<Ⅰ>. 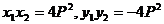 ; <Ⅱ>.
; <Ⅱ>.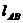 恒過(guò)定點(diǎn)
恒過(guò)定點(diǎn)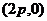 ;
;
<Ⅲ>. 中點(diǎn)軌跡方程:
中點(diǎn)軌跡方程: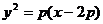 ;<Ⅳ>.
;<Ⅳ>.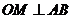 ,則
,則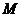 軌跡方程為:
軌跡方程為: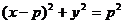 ;<Ⅴ>.
;<Ⅴ>.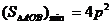 。
。
③拋物線y2=2px(p>0),對(duì)稱軸上一定點(diǎn)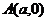 ,則:
,則:
<Ⅰ>.當(dāng)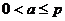 時(shí),頂點(diǎn)到點(diǎn)A距離最小,最小值為
時(shí),頂點(diǎn)到點(diǎn)A距離最小,最小值為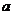 ;<Ⅱ>.當(dāng)
;<Ⅱ>.當(dāng)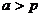 時(shí),拋物線上有關(guān)于
時(shí),拋物線上有關(guān)于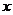 軸對(duì)稱的兩點(diǎn)到點(diǎn)A距離最小,最小值為
軸對(duì)稱的兩點(diǎn)到點(diǎn)A距離最小,最小值為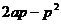 。
。
1.定義:⑴橢圓: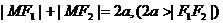 ;
;
⑵雙曲線: ;⑶拋物線:略
;⑶拋物線:略
10.與圓有關(guān)的結(jié)論:
⑴過(guò)圓x2+y2=r2上的點(diǎn)M(x0,y0)的切線方程為:x0x+y0y=r2;
過(guò)圓(x-a)2+(y-b)2=r2上的點(diǎn)M(x0,y0)的切線方程為:(x0-a)(x-a)+(y0-b)(y-b)=r2;
⑵以A(x1,y2)、B(x2,y2)為直徑的圓的方程:(x-x1)(x-x2)+(y-y1)(y-y2)=0。
9.點(diǎn)、直線與圓的位置關(guān)系:(主要掌握幾何法)
⑴點(diǎn)與圓的位置關(guān)系:(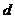 表示點(diǎn)到圓心的距離)
表示點(diǎn)到圓心的距離)
①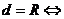 點(diǎn)在圓上;②
點(diǎn)在圓上;②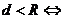 點(diǎn)在圓內(nèi);③
點(diǎn)在圓內(nèi);③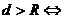 點(diǎn)在圓外。
點(diǎn)在圓外。
⑵直線與圓的位置關(guān)系:(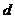 表示圓心到直線的距離)
表示圓心到直線的距離)
①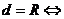 相切;②
相切;②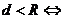 相交;③
相交;③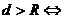 相離。
相離。
⑶圓與圓的位置關(guān)系:(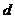 表示圓心距,
表示圓心距,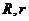 表示兩圓半徑,且
表示兩圓半徑,且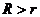 )
)
①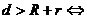 相離;②
相離;②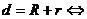 外切;③
外切;③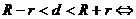 相交;
相交;
④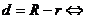 內(nèi)切;⑤
內(nèi)切;⑤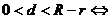 內(nèi)含。
內(nèi)含。
8.圓系:⑴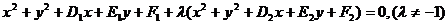 ;
;
注:當(dāng)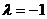 時(shí)表示兩圓交線。
時(shí)表示兩圓交線。
⑵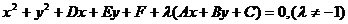 。
。
7.圓的方程的求法:⑴待定系數(shù)法;⑵幾何法;⑶圓系法。
6.圓的方程:⑴標(biāo)準(zhǔn)方程:①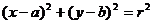 ;②
;②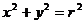 。
。
⑵一般方程: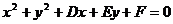 (
(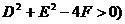
注:Ax2+Bxy+Cy2+Dx+Ey+F=0表示圓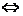 A=C≠0且B=0且D2+E2-4AF>0;
A=C≠0且B=0且D2+E2-4AF>0;
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com