
題目列表(包括答案和解析)
3、a>1時,不等式|x+logax|<|x|+|logax|的解集是 ( )
(A){x|0<x<a} (B){x|0<x<1}
(C){x|x>0} (D){x|x<0或x>1}
2、關于x的不等式(k2-2k+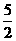 )x<(k2-2k+
)x<(k2-2k+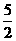 )1–x的解集是 ( )
)1–x的解集是 ( )
(A)x>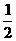 (B)x<
(B)x<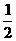 (C)x>2
(D)x<2
(C)x>2
(D)x<2
1、不等式lgx2<lg2x的解集是 ( )
(A)(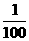 ,1)
(B)(100,+∞)
,1)
(B)(100,+∞)
(C)(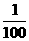 ,1)∪(100,+∞)
(D)(0,1)∪(100,+∞)
,1)∪(100,+∞)
(D)(0,1)∪(100,+∞)
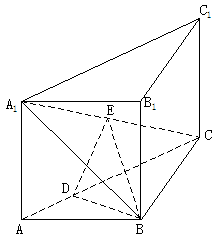
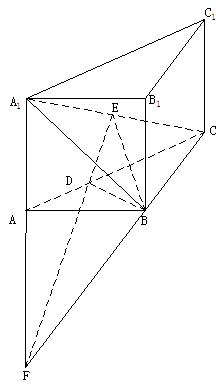
19.直三棱柱ABC-A1B1C1中, ,E是A1C的中點,
,E是A1C的中點,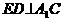 且交AC于D,
且交AC于D,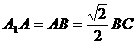 。
。
(I)證明: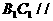 平面
平面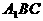 ;
;
(II)證明: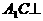 平面
平面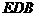 ;
;
(III)求平面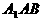 與平面EDB所成的二面角的大小(僅考慮平面角為銳角的情況)。
與平面EDB所成的二面角的大小(僅考慮平面角為銳角的情況)。
(I)證:
 三棱柱
三棱柱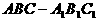 中
中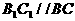 , 1分
, 1分
又 平面
平面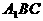 ,且
,且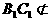 平面
平面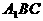 ,
,
 平面
平面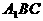 3分
3分
(II)證:
 三棱柱
三棱柱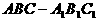 中
中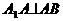 ,
,
 中
中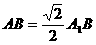
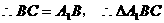 是等腰三角形 6分
是等腰三角形 6分
 E是等腰
E是等腰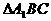 底邊
底邊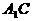 的中點,
的中點,
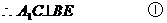
又依條件知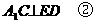
且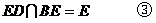
由①,②,③得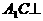 平面EDB 8分
平面EDB 8分
(III)解:
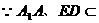 平面
平面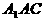 ,
,
且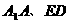 不平行,
不平行,
故延長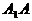 ,ED后必相交,
,ED后必相交,
設交點為E,連接EF,如下圖
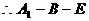 是所求的二面角 10分
是所求的二面角 10分
依條件易證明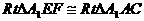
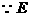 為
為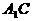 中點,
中點,
 A為
A為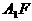 中點
中點
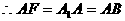
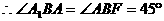
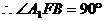
即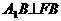 12分
12分
又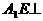 平面EFB,
平面EFB,

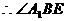 是所求的二面角的平面角 13分
是所求的二面角的平面角 13分
 E為等腰直角三角形
E為等腰直角三角形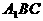 底邊中點,
底邊中點,
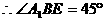
故所求的二面角的大小為 14分
14分
18.
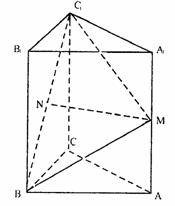 如圖,在直三棱柱ABC-A1B1C1中,AC=BC=2,AA1=2
如圖,在直三棱柱ABC-A1B1C1中,AC=BC=2,AA1=2 ,∠ACB=90°,M是AA1的中點,N是BC1中點.
,∠ACB=90°,M是AA1的中點,N是BC1中點.
(Ⅰ)求證:MN∥平面A1B1C1;
(Ⅱ)求二面角B-C1M-A的大小.
解:方法一(Ⅰ)取B1C1中點D,連結ND,A1D,
所以DN//BB1///AA1,………………1分
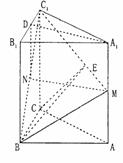 又,
又,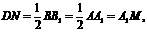 所以四邊形A1MND為平行四邊形,
所以四邊形A1MND為平行四邊形,
所以MN//A1D;…………3分
又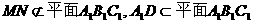 ,
,
所以MN//平面A1B1C1;…………5分
(Ⅱ)三棱柱ABC-A1B1C1為直三棱柱,所以CC1⊥BC,
又∠ACB=90°,所以BC⊥平面ACC1A1,…………7分
在平面ACC1A1上作CE⊥C1M,交C1M于點E.
則CE為BE在平面ACC1A1上的射影,
所以∠BEC為二面角B-C1M-A的平面角.………………9分
由于△CEC1與三角形C1A1M相似,所以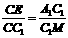
所以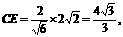 ……………………11分
……………………11分
所以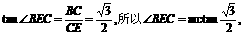 ……………………13分
……………………13分
 即二面角B-C1M-A的大小為
即二面角B-C1M-A的大小為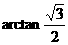 .…………………14分
.…………………14分
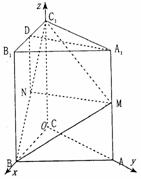
方法二(Ⅰ)如圖,以點C為坐標原點,以CB所在
直線為Ox軸,CA所在直線為Oy軸,CC1所在直線
為Oz軸,建立空間直角坐標系.
由已知得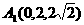 、
、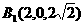 、
、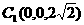 .
.
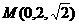 ,
,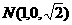 ,
,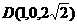
所以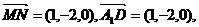
所以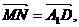 …………2分
所以MN//A1N;………………4分
…………2分
所以MN//A1N;………………4分
又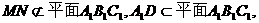 所以MN//平面A1B1C1;…………5分
所以MN//平面A1B1C1;…………5分
(Ⅱ)三棱柱ABC-A1B1C1為直三棱柱,所以CC1⊥BC,
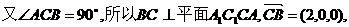 ………………7分
………………7分
設垂直于平面BMC1的向量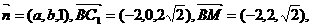
所以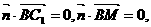 即
即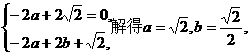
所以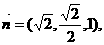 ……………………………………10分
……………………………………10分
所求二面角的大小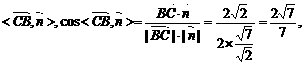 ……………13分
……………13分
即二面角B-C1M-A的大小為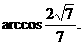 …………………………14分
…………………………14分
17.在學校的科技活動日中,有六件科技作品在展臺上排成一排展出.
(Ⅰ)求作品甲不在兩端的概率;
(Ⅱ)求作品甲、乙相鄰的概率.
解(Ⅰ)作品甲不在兩端的概率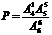 ……………………5分
……………………5分
=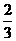 ;……………………6分
;……………………6分
(Ⅱ)作品甲、乙相鄰的概率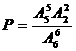 ……………………11分
……………………11分
作品甲、乙相鄰的概率為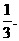 …………………………12分
…………………………12分
16.已知點P,直線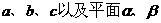 ,給出下列命題:
,給出下列命題:
①若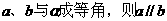 ②若
②若
③若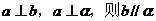 ④若
④若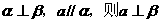
⑤若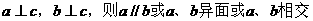
其中正確命題的序號是_____②⑤________(把所有正確命題的序號都填上)。
15.將棱長為1的正方體木塊加工成一個體積最大的球,則這個球的體積為____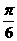 ___,球的表面積為__
___,球的表面積為__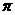 ________(不計損耗)。
________(不計損耗)。
14.三角形ABC的斜邊AB在平面a內,直角邊AC,BC與平面a所成的角分別為 30°、60°,則平面ABC與平面a所成的二面角的正弦值為______ 1________.
13.現有甲種電腦56臺,乙種電腦42臺,如果用分層抽樣的方法從中抽取一個容量為14的樣本,則乙種電腦應抽樣___6_____臺.
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com