
青島市2009年高三模擬練習
數學(理科) 2009.05
本試卷分第Ⅰ卷(選擇題)和第Ⅱ卷(非選擇題)兩部分.共150分.考試時間120分鐘.
注意事項:
1.答卷前,考生務必用2B鉛筆和0.5毫米黑色簽字筆(中性筆)將姓名、準考證號、考試科目、試卷類型填涂在答題卡規定的位置上.
2.第Ⅰ卷每小題選出答案后,用2B鉛筆把答題卡上對應的答案標號涂黑;如需改動,用橡皮擦干凈后,再選涂其他答案標號.答案不能答在試題卷上.
3.第Ⅱ卷必須用0.5毫米黑色簽字筆(中性筆)作答,答案必須寫在答題卡各題目指定區域內相應的位置,不能寫在試題卷上;如需改動,先劃掉原來的答案,然后再寫上新的答案;不準使用涂改液、膠帶紙、修正帶。不按以上要求作答的答案無效.
第Ⅰ卷(選擇題 共60分)
一、選擇題:本大題共12小題.每小題5分,共60分.在每小題給出的四個選項中,只有一項是符合題目要求的.
1. 已知集合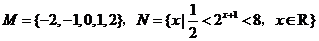 ,則
,則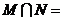
A.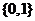 B.
B.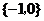 C.
C.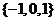 D.
D.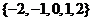
2.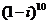
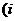 為虛數單位
為虛數單位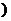 的二項展開式中第七項為
的二項展開式中第七項為
A.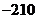 B.
B.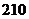 C.
C.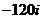 D.
D.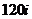
3. 設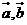 都是非零向量,那么命題“
都是非零向量,那么命題“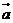 與
與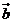 共線”是命題“
共線”是命題“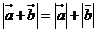 ”的
”的
A. 充分不必要條件 B. 必要不充分條件 C. 充要條件 D. 既不充分又不必要條件
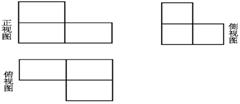 4.如右圖為長方體木塊堆成的幾何體的三視圖,
4.如右圖為長方體木塊堆成的幾何體的三視圖,
則組成此幾何體的長方體木塊塊數共有
A.3塊 B.4塊 C.5塊 D.6塊
5. 已知各項不為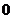 的等差數列
的等差數列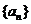 ,滿足
,滿足
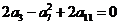 ,數列
,數列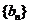 是等比數列,且
是等比數列,且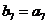 ,則
,則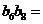
A.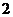 B.
B.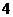 C.
C.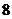 D.
D.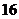
6.汽車經過啟動、加速行駛、勻速行駛、減速行駛之后停車,若把這一過程中汽車的行駛路程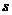 看作時間
看作時間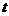 的函數,其圖象可能是
的函數,其圖象可能是
 |
7. 已知雙曲線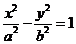 的一條漸近線方程為
的一條漸近線方程為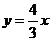 ,則雙曲線的離心率為
,則雙曲線的離心率為
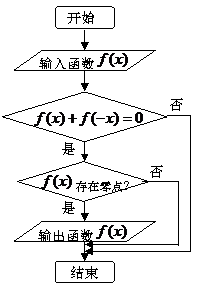 A.
A.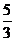 B.
B.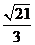 C.
C.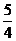 D.
D.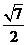
8.某程序框圖如右圖所示,現輸入如下四個函數,則可以輸出的函數是
A.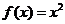 B.
B.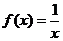
C.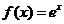 D.
D.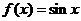
9.如右下圖,在一個長為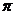 ,寬為2的矩形
,寬為2的矩形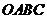 內,曲線
內,曲線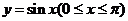 與
與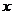 軸圍成如圖所示的陰影部分,向矩形
軸圍成如圖所示的陰影部分,向矩形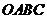 內隨機投一點(該點落在矩形
內隨機投一點(該點落在矩形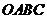 內任何一點是等可能的),則所投的點落在陰影部分的概率是
內任何一點是等可能的),則所投的點落在陰影部分的概率是
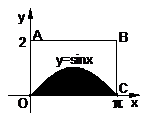 A.
A.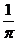 B.
B.  C.
C.
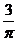 D.
D.
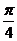
10. 已知直線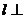 平面
平面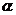 ,直線
,直線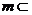 平面
平面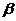 ,給出下列命題中
,給出下列命題中
①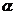 ∥
∥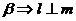 ;②
;②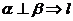 ∥
∥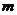 ;
;
③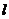 ∥
∥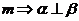 ;④
;④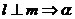 ∥
∥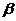 .其中正確的是
.其中正確的是
A.①②③ B.②③④ C.②④ D.①③
 11. 已知
11. 已知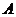 船在燈塔
船在燈塔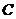 北偏東
北偏東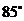 且
且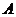 到
到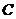 的距離為
的距離為 ,
,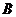 船在燈塔
船在燈塔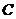 西偏北
西偏北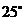 且
且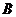 到
到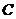 的距離為
的距離為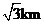 ,則
,則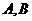 兩船的距離為
兩船的距離為
A. 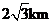 B.
B. 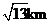 C.
C. 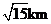 D.
D.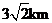
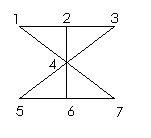
12.把3盆不同的蘭花和4盆不同的玫瑰花擺放在右圖圖案中的
 所示的位置上,其中三盆蘭花不能放在一條直線上,
所示的位置上,其中三盆蘭花不能放在一條直線上,
則不同的擺放方法為
A.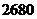 種 B.
種 B.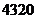 種 C.
種 C.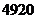 種 D.
種 D. 種
種
第Ⅱ卷(非選擇題 共90分)
二、填空:本大題共4小題,每小題4分,共16分.
 |
則第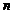 個圖案中有白色地面磚的塊數是
.
個圖案中有白色地面磚的塊數是
.
14.已知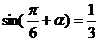 ,則
,則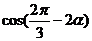 的值等于
.
的值等于
.
15.已知函數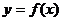
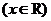 滿足
滿足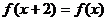 ,且
,且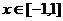 時,
時,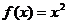 ,則
,則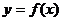 與
與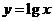 的圖象的交點個數為
.高考資源網
的圖象的交點個數為
.高考資源網
16.若不等式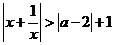 對于一切非零實數
對于一切非零實數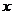 均成立,則實數
均成立,則實數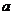 的取值范圍是
的取值范圍是
.
三、解答題:本大題共6小題,共74分,解答時應寫出必要的文字說明、證明過程或演算步驟.
17.(本小題滿分12分)
已知向量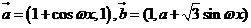 (
(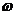 為常數且
為常數且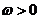 ),函數
),函數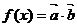 在
在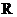 上的最大值為
上的最大值為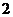 .
.
(Ⅰ)求實數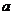 的值;
的值;
(Ⅱ)把函數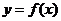 的圖象向右平移
的圖象向右平移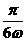 個單位,可得函數
個單位,可得函數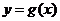 的圖象,若
的圖象,若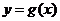 在
在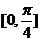 上為增函數,求
上為增函數,求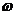 的最大值.
的最大值.
18. (本小題滿分12分)
某種食品是經過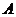 、
、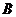 、
、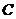 三道工序加工而成的,
三道工序加工而成的,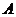 、
、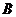 、
、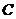 工序的產品合格率分別為
工序的產品合格率分別為 、
、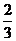 、
、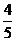 .已知每道工序的加工都相互獨立,三道工序加工的產品都為合格時產品為一等品;有兩次合格為二等品;其它的為廢品,不進入市場.
.已知每道工序的加工都相互獨立,三道工序加工的產品都為合格時產品為一等品;有兩次合格為二等品;其它的為廢品,不進入市場.
(Ⅰ)正式生產前先試生產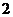 袋食品,求這2袋食品都為廢品的概率;
袋食品,求這2袋食品都為廢品的概率;
(Ⅱ)設 為加工工序中產品合格的次數,求
為加工工序中產品合格的次數,求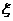 的分布列和數學期望.
的分布列和數學期望.
19.(本小題滿分12分)
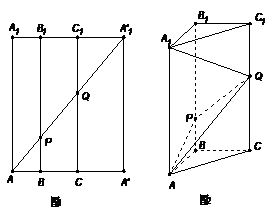 如圖1所示,在邊長為
如圖1所示,在邊長為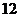 的正方形
的正方形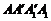 中,
中,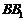
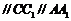 ,且
,且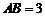 ,
,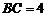 ,
,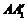 分別交
分別交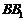
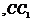 點于
點于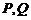 ,將該正方形沿
,將該正方形沿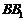 、
、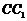 折疊,使得
折疊,使得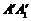 與
與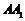 重合,構成如圖2所示的三棱柱
重合,構成如圖2所示的三棱柱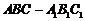 中
中
(Ⅰ)求證: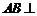
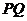 ;
;
(Ⅱ)在底邊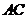 上有一點
上有一點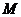 ,
,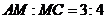 ,
,
求證: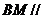 面
面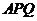
(III)求直線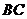 與平面
與平面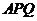 所成角的正弦值.
所成角的正弦值.
20.(本小題滿分12分)
在數列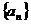 中,
中,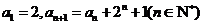 .
.
(Ⅰ)求證:數列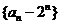 為等差數列;
為等差數列;
(Ⅱ)設數列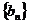 滿足
滿足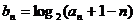 ,若
,若
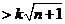 對一切
對一切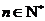 且
且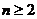 恒成立,求實數
恒成立,求實數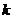 的取值范圍.
的取值范圍.
21.(本小題滿分12分)已知函數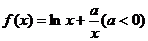 ,直線
,直線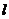 與函數
與函數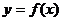 圖象相切.
圖象相切.
(Ⅰ)求直線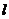 的斜率
的斜率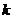 的取值范圍;
的取值范圍;
(Ⅱ)設函數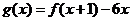 ,已知函數
,已知函數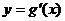 的圖象經過點
的圖象經過點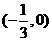 ,求函數
,求函數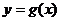 的極值.
的極值.
22. (本小題滿分14分)已知兩點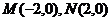 ,點
,點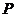 為坐標平面內的動點,且滿足
為坐標平面內的動點,且滿足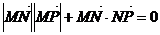 .
.
(Ⅰ)求點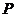 的軌跡
的軌跡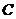 的方程;
的方程;
(Ⅱ)設過點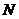 的直線
的直線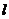 斜率為
斜率為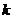 ,且與曲線
,且與曲線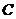 相交于點
相交于點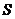 、
、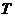 ,若
,若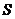 、
、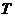 兩點只在第二象限內運動,線段
兩點只在第二象限內運動,線段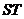 的垂直平分線交
的垂直平分線交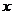 軸于
軸于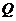 點,求
點,求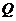 點橫坐標的取值范圍.
點橫坐標的取值范圍.
青島市2009年高三模擬練習
數學(理科)答案及評分標準 2009.05
CABBD,AADAD,BB
二、填空:本大題共4小題,每小題4分,共16分.
13.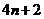 ; 14.
; 14.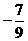 ; 15.
; 15.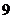 ; 16.
; 16.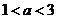
三、解答題:本大題共6小題,共74分,解答時應寫出必要的文字說明、證明過程或演算步驟.
17.(本小題滿分12分)
解:(Ⅰ)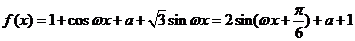 ………3分
………3分
因為函數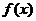 在
在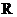 上的最大值為
上的最大值為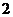 ,所以
,所以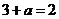 故
故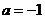 …………5分
…………5分
(Ⅱ)由(Ⅰ)知: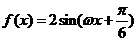
把函數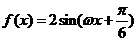 的圖象向右平移
的圖象向右平移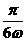 個單位,
個單位,
可得函數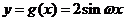 …………………………………………8分
…………………………………………8分
又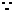
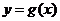 在
在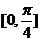 上為增函數
上為增函數
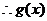 的周期
的周期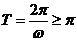 即
即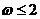
所以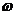 的最大值為
的最大值為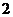 …………………………12分
…………………………12分
18. (本小題滿分12分)
解:(Ⅰ)2袋食品都為廢品的情況為
①2袋食品的三道工序都不合格
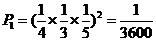 ……………2分
……………2分
②有一袋食品三道工序都不合格,另一袋有兩道工序不合格
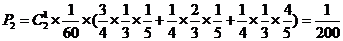 ……………4分
……………4分
③兩袋都有兩道工序不合格
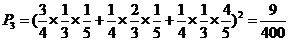
所以2袋食品都為廢品的概率為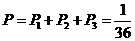 ……………6分
……………6分
(Ⅱ)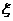
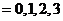
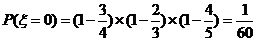
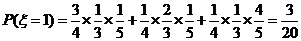 ………8分
………8分
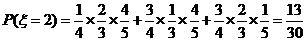
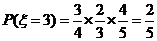 ………10分
………10分
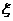
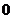
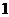
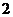
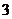
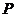
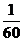
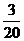
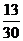
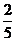
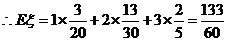 ………12分
………12分
19.(本小題滿分12分)
(Ⅰ)證明:因為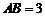 ,
,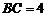 ,
,
所以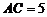 ,從而
,從而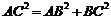 ,即
,即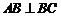 .………………………2分
.………………………2分
又因為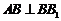 ,而
,而 ,
,
所以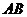
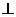 平面
平面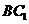 又
又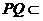 平面
平面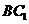
所以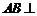
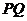 ;………………4分
;………………4分
(Ⅱ)解:過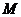 作
作 交
交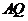 于
于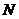 ,連接
,連接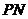 ,
,
因為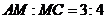
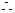
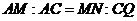
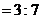 ……………6分
……………6分
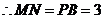
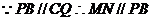
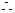 四邊形
四邊形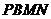 為平行四邊形
為平行四邊形
 ,所以
,所以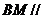 平面
平面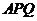 …………………………8分
…………………………8分
(III)解:由圖1知,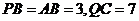 ,分別以
,分別以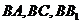 為
為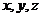 軸,
軸,
則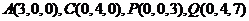
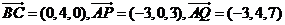 ………10分
………10分
設平面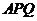 的法向量為
的法向量為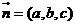 ,
,
所以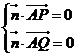 得
得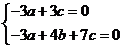 ,
,
令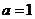 ,則
,則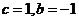 ,
,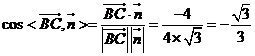
所以直線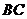 與平面
與平面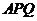 所成角的正弦值為
所成角的正弦值為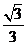 …………………………12分
…………………………12分
20.(本小題滿分12分)
解:(Ⅰ) 由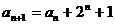 變形得:
變形得: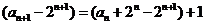
即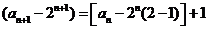
所以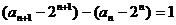 …………………4分
…………………4分
故數列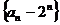 是以
是以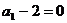 為首項,
為首項,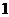 為公差的等差數列………………………5分
為公差的等差數列………………………5分
(Ⅱ)由(Ⅰ)得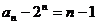 …………………………6分
…………………………6分
所以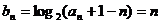 …………………………7分
…………………………7分
設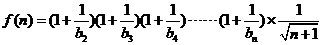 ………………8分
………………8分
則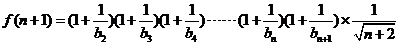
兩式相除得: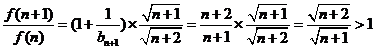 ……10分
……10分
所以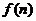 是關于
是關于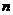 的單調遞增函數,則
的單調遞增函數,則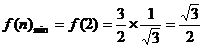
故實數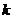 的取值范圍是
的取值范圍是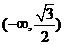 …………………………12分
…………………………12分
21.(本小題滿分12分)
解:(Ⅰ)設切點坐標為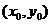 ,由
,由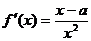 ………………………2分
………………………2分
則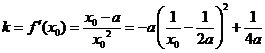 …………………………4分
…………………………4分
根據題意知: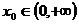 ,即
,即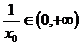 ,所以
,所以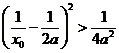
又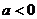 ,則
,則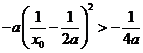 ,即
,即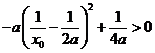
所以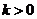 …………………………6分
…………………………6分
(Ⅱ)顯然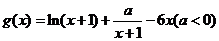 的定義域為
的定義域為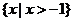 ………7分
………7分
則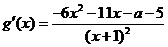 ………………………8分
………………………8分
又因為函數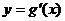 的圖象經過點
的圖象經過點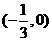 ,代入
,代入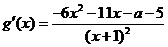
求得: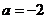 ,則
,則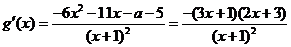 ……………10分
……………10分
由此可知:當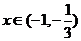 時,有
時,有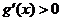 ,此時
,此時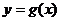 為單調增函數;
為單調增函數;
當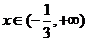 時,有
時,有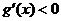 ,此時
,此時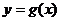 為單調減函數;
為單調減函數;
所以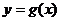 在區間
在區間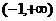 上只有極大值即
上只有極大值即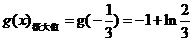 …12分
…12分
22. (本小題滿分14分)
解:(Ⅰ)設點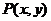 ,根據題意則有:
,根據題意則有:
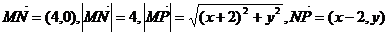
代入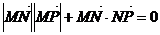 得:
得: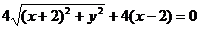 …………3分
…………3分
整理得點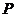 的軌跡
的軌跡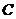 的方程
的方程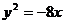 …………………………5分
…………………………5分
(Ⅱ)設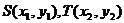
由題意得: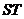 的方程為
的方程為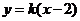 (顯然
(顯然 )
)
與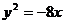 聯立消元得:
聯立消元得: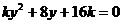 …………………………7分
…………………………7分
則有: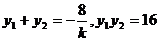
再由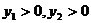 ,則
,則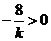 ,得
,得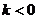 ………………………8分
………………………8分
可求得線段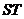 中點
中點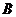 的坐標為
的坐標為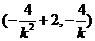
所以線段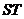 的垂直平分線方程為
的垂直平分線方程為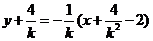 …………………………10分
…………………………10分
令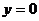 得點
得點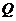 橫坐標為
橫坐標為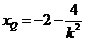
因為直線交軌跡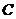 于兩點,
于兩點, ,所以
,所以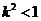 ………12分
………12分
所以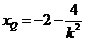
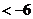
所以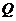 點橫坐標的取值范圍為
點橫坐標的取值范圍為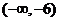 …………14分
…………14分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com