
1.(1)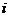 -1
-1 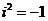
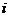 -1
-1 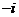 1 (2)
1 (2)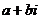 實數 虛部 純虛數
實數 虛部 純虛數
(3)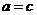 且
且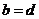
22.解:(1)由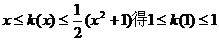 ,所以
,所以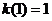
(2)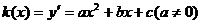 ,由
,由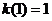 ,
,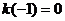 得
得
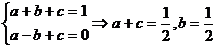
又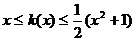 恒成立,則由
恒成立,則由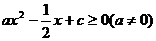 恒成立得
恒成立得
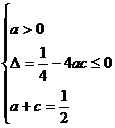
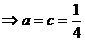 ,
,
同理由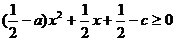 恒成立也可得:
恒成立也可得: 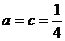
綜上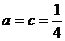 ,
,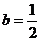 ,所以
,所以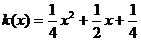
(3):(分析法)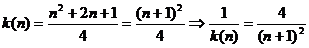
要證原不等式式,即證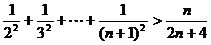
因為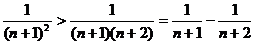
所以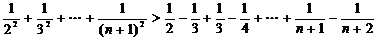
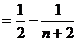 =
=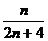
所以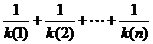
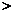
 。
。
第三章 數系的擴充與復數的引入
第一講 復數的相關概念和幾何意義
[知識梳理]
[知識盤點]
21.證明:假設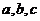 都不大于
都不大于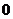 ,即
,即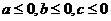 ,得
,得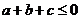 ,
,
而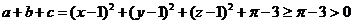 ,
,
即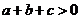 ,與
,與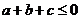 矛盾,
矛盾,
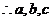 中至少有一個大于
中至少有一個大于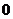 。
。
20.解:(1)由對稱軸是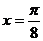 ,得
,得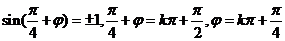 ,
,
而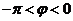 ,所以
,所以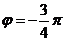
(2)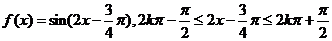
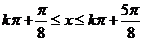 ,增區間為
,增區間為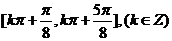
(3)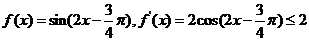 ,即曲線的切線的斜率不大于
,即曲線的切線的斜率不大于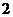 ,
,
而直線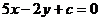 的斜率
的斜率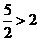 ,即直線
,即直線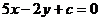 不是函數
不是函數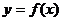 的切線。
的切線。
19.證明:連結AB,A1D,在正方形中,A1B=A1D,O是BD中點,∴A1O⊥BD;
連結OM,A1M,A1C1,設AB=a,則AA1=a,MC=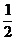 a=MC1,OA=OC=
a=MC1,OA=OC=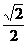 a,AC=
a,AC=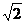 a,
a,
∴A1O2=A1A2+AO2=a2+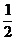 a2=
a2=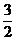 a2,OM2=OC2+MC2=
a2,OM2=OC2+MC2=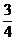 a2,A1M2=A1C12+MC12=2a2+
a2,A1M2=A1C12+MC12=2a2+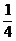 a2=
a2=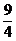 a2,
a2,
∴A1M2=A1O2+OM2,∴A1O⊥OM,∴AO1⊥平面MBD。
18.證明:要證明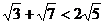 成立, 只需證
成立, 只需證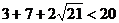 成立,
成立,
只需證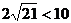 成立,只需證
成立,只需證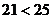 成立,上式顯然成立,所以原命題成立.
成立,上式顯然成立,所以原命題成立.
17.解:作差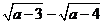
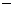 (
(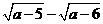 )=
)=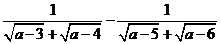
∵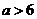 ,
,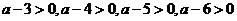 又∵
又∵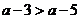 ∴
∴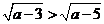
同樣地有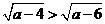 則
則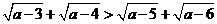
即知上式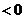 ∴
∴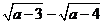 <
<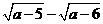
法二:令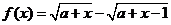 (
(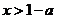 )
)
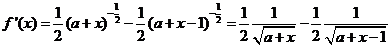 <0即知
<0即知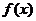 在定義域內為減函數,故
在定義域內為減函數,故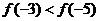 ,∴
,∴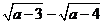 <
<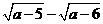
16. 和
和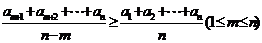
15.a+(a*b)=(a+b)*(a+c)(答案不惟一)
14.4
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com