
2008年天津市初中畢業生學業考試
數學試卷
第Ⅰ卷(選擇題 共30分)
一、選擇題:本大題共10小題,每小題3分,共30分.在每小題給出的四個選項中,只有一項是符合題目要求的.
1. 的值等于( )
的值等于( )
A. B.
B. C.
C. D.1
D.1
2.對稱現象無處不在,請你觀察下面的四個圖形,它們體現了中華民族的傳統文化,

其中,可以看作是軸對稱圖形的有( )
A.1個 B.2個 C.3個 D.4個
3.邊長為 的正六邊形的面積等于( )
的正六邊形的面積等于( )
A. B.
B. C.
C. D.
D.
4.納米是非常小的長度單位,已知1納米= 毫米,某種病毒的直徑為100納米,若將這種病毒排成1毫米長,則病毒的個數是(
)
毫米,某種病毒的直徑為100納米,若將這種病毒排成1毫米長,則病毒的個數是(
)
A. 個 B.
個 B. 個 C.
個 C. 個 D.
個 D. 個
個
5.把拋物線 向上平移5個單位,所得拋物線的解析式為( )
向上平移5個單位,所得拋物線的解析式為( )
A. B.
B. C.
C. D.
D.
6.擲兩枚質地均勻的硬幣,則兩枚硬幣全部正面朝上的概率等于( )
A.1 B. C.
C. D.0
D.0
7.下面的三視圖所對應的物體是( )


8.若 ,則估計
,則估計 的值所在的范圍是( )
的值所在的范圍是( )
A. B.
B. C.
C. D.
D.
9.在平面直角坐標系中,已知點A(0,2),B( ,0),C(0,
,0),C(0, ),D(
),D( ,0),則以這四個點為頂點的四邊形
,0),則以這四個點為頂點的四邊形 是( )
是( )
A.矩形 B.菱形 C.正方形 D.梯形
10.在平面直角坐標系中,已知點 (
( ,0),B(2,0),若點C在一次函數
,0),B(2,0),若點C在一次函數 的圖象上,且△ABC為直角三角形,則滿足條件的點C有( )
的圖象上,且△ABC為直角三角形,則滿足條件的點C有( )
A.1個 B.2個 C.3個 D.4個
第Ⅱ卷(非選擇題 共90分)
二、填空題:本大題共8小題,每小題3分,共24分.請將答案直接填在題中橫線上.
11.不等式組 的解集為
.
的解集為
.
12.若 ,則
,則 的值為
.
的值為
.
13.已知拋物線 ,若點
,若點 (
( ,5)與點
,5)與點 關于該拋物線的對稱軸對稱,則點
關于該拋物線的對稱軸對稱,則點 的坐標是
.
的坐標是
.
14.如圖,是北京奧運會、殘奧會賽會志愿者申請人來源的統計數據,請你計算:志愿者申請人的總數為 萬;其中“京外省區市”志愿者申請人數在總人數中所占的百分比約為 %(精確到0.1%),它所對應的扇形的圓心角約為 (度)(精確到度).

15.如圖,已知△ABC中,EF∥GH∥IJ∥BC,則圖中相似三角形共有 對.

16.如圖,在正方形ABCD中,E為AB邊的中點,G,F分別為AD,BC邊上的點,若 ,
, ,
, ,則GF的長為 .
,則GF的長為 .

17.已知關于x的函數同時滿足下列三個條件:
①函數的圖象不經過第二象限;
②當 時,對應的函數值
時,對應的函數值 ;
;
③當 時,函數值y隨x的增大而增大.
時,函數值y隨x的增大而增大.
你認為符合要求的函數的解析式可以是: (寫出一個即可).
18.如圖①, ,
, ,
, ,
, 為四個等圓的圓心,A,B,C,D為切點,請你在圖中畫出一條直線,將這四個圓分成面積相等的兩部分,并說明這條直線經過的兩個點是
;如圖②,
為四個等圓的圓心,A,B,C,D為切點,請你在圖中畫出一條直線,將這四個圓分成面積相等的兩部分,并說明這條直線經過的兩個點是
;如圖②, ,
, ,
, ,
, ,
, 為五個等圓的圓心,A,B,C,D,E為切點,請你在圖中畫出一條直線,將這五個圓分成面積相等的兩部分,并說明這條直線經過的兩個點是
.
為五個等圓的圓心,A,B,C,D,E為切點,請你在圖中畫出一條直線,將這五個圓分成面積相等的兩部分,并說明這條直線經過的兩個點是
.

三、解答題:本大題共8小題,共66分.解答應寫出文字說明、演算步驟或證明過程.
19.(本小題6分)
解二元一次方程組
20.(本小題8分)
已知點P(2,2)在反比例函數 (
( )的圖象上,
)的圖象上,
(Ⅰ)當 時,求
時,求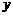 的值;
的值;
(Ⅱ)當 時,求
時,求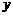 的取值范圍.
的取值范圍.
21.(本小題8分)
如圖,在梯形ABCD中,AB∥CD,⊙O為內切圓,E為切點,
(Ⅰ)求 的度數;
的度數;
(Ⅱ)若 cm,
cm, cm,求OE的長.
cm,求OE的長.

22.(本小題8分)
下圖是交警在一個路口統計的某個時段來往車輛的車速情況(單位:千米/時).

請分別計算這些車輛行駛速度的平均數、中位數和眾數(結果精確到0.1).
23.(本小題8分)
熱氣球的探測器顯示,從熱氣球看一棟高樓頂部的仰角為 ,看這棟高樓底部的俯角為
,看這棟高樓底部的俯角為 ,熱氣球與高樓的水平距離為
,熱氣球與高樓的水平距離為 )
)

24.(本小題8分)注意:為了使同學們更好地解答本題,我們提供了一種解題思路,你可以依照這個思路,填寫表格,并完成本題解答的全過程.如果你選用其他的解題方案,此時,不必填寫表格,只需按照解答題的一般要求,進行解答即可.
天津市奧林匹克中心體育場――“水滴”位于天津市西南部的奧林匹克中心內,某校九年級學生由距“水滴”
(Ⅰ)設騎車同學的速度為x千米/時,利用速度、時間、路程之間的關系填寫下表.
(要求:填上適當的代數式,完成表格)
速度(千米/時)
所用時間(時)
所走的路程(千米)
騎自行車


10
乘汽車
10
(Ⅱ)列出方程(組),并求出問題的解.
25.(本小題10分)
已知Rt△ABC中, ,
, ,有一個圓心角為
,有一個圓心角為 ,半徑的長等于
,半徑的長等于 的扇形
的扇形 繞點C旋轉,且直線CE,CF分別與直線
繞點C旋轉,且直線CE,CF分別與直線 交于點M,N.
交于點M,N.
(Ⅰ)當扇形 繞點C在
繞點C在 的內部旋轉時,如圖①,求證:
的內部旋轉時,如圖①,求證: ;
;
思路點撥:考慮 符合勾股定理的形式,需轉化為在直角三角形中解決.可將△
符合勾股定理的形式,需轉化為在直角三角形中解決.可將△ 沿直線
沿直線 對折,得△
對折,得△ ,連
,連 ,只需證
,只需證 ,
, 就可以了.
就可以了.
請你完成證明過程:

(Ⅱ)當扇形CEF繞點C旋轉至圖②的位置時,關系式 是否仍然成立?若成立,請證明;若不成立,請說明理由.
是否仍然成立?若成立,請證明;若不成立,請說明理由.

26.(本小題10分)
已知拋物線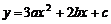 ,
,
(Ⅰ)若 ,
, ,求該拋物線與
,求該拋物線與 軸公共點的坐標;
軸公共點的坐標;
(Ⅱ)若 ,且當
,且當 時,拋物線與
時,拋物線與 軸有且只有一個公共點,求
軸有且只有一個公共點,求 的取值范圍;
的取值范圍;
(Ⅲ)若 ,且
,且 時,對應的
時,對應的 ;
; 時,對應的
時,對應的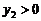 ,試判斷當
,試判斷當 時,拋物線與
時,拋物線與 軸是否有公共點?若有,請證明你的結論;若沒有,闡述理由.
軸是否有公共點?若有,請證明你的結論;若沒有,闡述理由.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com