精品一区二区免费在线观看_国产精品久久久久久av福利软件_97成人精品区在线播放_国内成人精品一区

如圖，拋物線與軸交于A、B兩點（點A在點B左側(cè)），與y軸交

于點C，且當(dāng)=0和=4時，y的值相等。直線y=4x-16與這條拋物線相交于兩點，其中一點的橫坐標(biāo)是3，另一點是這條拋物線的頂點M。

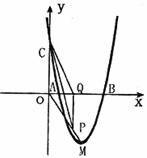
（1）求這條拋物線的解析式；

（2）P為線段OM上一點，過點P作PQ⊥軸于點Q。若點P在線段OM上運動（點P不與點O重合，但可以與點M重合），設(shè)OQ的長為t，四邊形PQCO的面積為S，求S與t之間的函數(shù)關(guān)系式及自變量t的取值范圍；

（3）隨著點P的運動，四邊形PQCO的面積S有最大值嗎？如果S有最大值，請求出S的最大值并指出點Q的具體位置和四邊形PQCO的特殊形狀；如果S沒有最大值，請簡要說明理由；

（4）隨著點P的運動，是否存在t的某個值，能滿足PO=OC？如果存在，請求出t的值。

如圖，拋物線與軸交于（，0）、（，0）兩點，且，與軸交于點，其中是方程的兩個根。

（1）求拋物線的解析式；

（2）點是線段上的一個動點，過點作∥，交于點，連接，當(dāng)的面積最大時，求點的坐標(biāo)；

（3）點在（1）中拋物線上，點為拋物線上一動點，在軸上是否存在點，使以為頂點的四邊形是平行四邊形，如果存在，求出所有滿足條件的點的坐標(biāo)，若不存在，請說明理由。

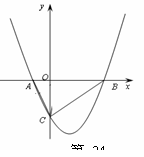
如圖，拋物線與軸交于、(6 , 0)兩點，且對稱軸為直線x = 2，與軸交于點。

（1）求拋物線的解析式；

（2）點是拋物線對稱軸上的一個動點，連接MA、MC，

當(dāng)△MAC的周長最小時，求點的坐標(biāo)；

（3）點在（1）中拋物線上，點為拋物線上一

動點，在軸上是否存在點，使以為頂點的四邊形是平行四邊形，如果存在，直接寫出所有

滿足條件的點的坐標(biāo)，若不存在，請說明理由。

如圖，拋物線與軸交于（，0）、（，0）兩點，且，與軸交于點，其中是方程的兩個根。

（1）求拋物線的解析式；

（2）點是線段上的一個動點，過點作∥，交于點，連接，當(dāng)的面積最大時，求點的坐標(biāo)；

（3）點在（1）中拋物線上，點為拋物線上一動點，在軸上是否存在點，使以為頂點的四邊形是平行四邊形，如果存在，求出所有滿足條件的點的坐標(biāo)，若不存在，請說明理由。

如圖，拋物線與軸交于（，0）、（，0）兩點，且，與軸交于點，其中是方程的兩個根。（14分）

（1）求拋物線的解析式；

（2）點是線段上的一個動點，過點作∥，交于點，連接，當(dāng)的面積最大時，求點的坐標(biāo)；

（3）點在（1）中拋物線上，點為拋物線上一動點，在軸上是否存在點，使以為頂點的四邊形是平行四邊形，如果存在，求出所有滿足條件的點的坐標(biāo)，若不存在，請說明理由。