
第一講 函數定義域和值域
★★★高考在考什么
【考題回放】
1.函數f(x)= 的定義域是 ( A )
的定義域是 ( A )
A. -∞,0] B.[0,+∞
-∞,0] B.[0,+∞ C.(-∞,0) D.(-∞,+∞)
C.(-∞,0) D.(-∞,+∞)
2.函數 的定義域為 (A )
的定義域為 (A )
A.(1,2)∪(2,3) B.
C.(1,3) D.[1,3]
3. 對于拋物線線 上的每一個點
上的每一個點 ,點
,點 都滿足
都滿足 ,則
,則 的取值范圍是
( B )
的取值范圍是
( B )
 .
.
 .
.
 .
.
 .
.
4.已知 的定義域為
的定義域為 ,則
,則 的定義域為
的定義域為  。
。
5. 不等式 對一切非零實數x總成立 , 則
對一切非零實數x總成立 , 則 的取值范圍是
的取值范圍是
 __。
__。
6. 已知二次函數 的導數為
的導數為 ,
, ,對于任意實數
,對于任意實數 ,有
,有 ,則
,則 的最小值為 。
的最小值為 。
★★★高考要考什么
一、 函數定義域有兩類:具體函數與抽象函數
抽象函數:(1)已知 的定義域為D,求
的定義域為D,求 的定義域;(由
的定義域;(由 求得
求得 的范圍就是)
的范圍就是)
(2)已知 的定義域為D,求
的定義域為D,求 的定義域;(
的定義域;( 求出
求出 的范圍就是)
的范圍就是)
二、 函數值域(最值)的求法有:
直觀法:圖象在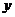 軸上的“投影”的范圍就是值域的范圍;
軸上的“投影”的范圍就是值域的范圍;
配方法:適合一元二次函數
反解法:有界量用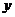 來表示。如
來表示。如 ,
, ,
, 等等。如,
等等。如, 。
。
換元法:通過變量代換轉化為能求值域的函數,特別注意新變量的范圍。注意三角換元的應用。
如求 的值域。
的值域。
單調性:特別適合于指、對數函數的復合函數。如求 值域。
值域。
注意函數 的單調性。
的單調性。
基本不等式:要注意“一正、二定、三相等”,
判別式:適合于可轉化為關于 的一元二次方程的函數求值域。如
的一元二次方程的函數求值域。如 。
。
反之:方程有解也可轉化為函數求值域。如方程 有解,求
有解,求 的范圍。
的范圍。
數形結合:要注意代數式的幾何意義。如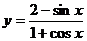 的值域。(幾何意義??斜率)
的值域。(幾何意義??斜率)
三、 恒成立和有解問題
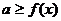 恒成立
恒成立 的最大值;
的最大值;
 恒成立
恒成立 的最小值;
的最小值;
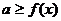 有解
有解 的最小值;
的最小值; 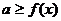 無解
無解 的最小值;
的最小值;
★★★ 突 破 重 難 點
【范例1】已知f(x)=3x-b(2≤x≤4,b為常數)的圖象經過點(2,1),求F(x)=[f-1(x)]2-f-1(x2)的值域。
分析提示:求函數值域時,不但要重視對應法則的作用,而且要特別注意定義域的制約作用。本題要注意F(x)的定義域與f-1(x)定義域的聯系與區別。
解:由圖象經過點(2,1)得, ,
, 


 F(x)=[f-1(x)]2-f-1(x2)
F(x)=[f-1(x)]2-f-1(x2) 
 的定義域為
的定義域為 

 ,
,  ,
,  的值域是
的值域是
變式: 函數 的定義域為
的定義域為 ,圖象如圖所示,
,圖象如圖所示,
其反函數為 則不等式
則不等式
的解集為  .
.
【范例2】設函數 .
.
(Ⅰ)求 的最小值
的最小值 ;
;
(Ⅱ)若 對
對 恒成立,求實數
恒成立,求實數 的取值范圍.
的取值范圍.
解:(Ⅰ) ,
,
 當
當 時,
時, 取最小值
取最小值 ,
,
即 .
.
(Ⅱ)令 ,
,
由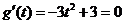 得
得 ,
, (不合題意,舍去).
(不合題意,舍去).
當 變化時
變化時 ,
, 的變化情況如下表:
的變化情況如下表:

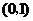







遞增
極大值
遞減
 在
在 內有最大值
內有最大值 .
.
 在
在 內恒成立等價于
內恒成立等價于 在
在 內恒成立,
內恒成立,
即等價于 ,
,
所以 的取值范圍為
的取值范圍為 .
.
變式:函數f(x)是奇函數,且在[―l,1]上單調遞增,f(-1)=-1,(1) 則f(x)在[-1,1]上的最大值 1
,(2) 若 對所有的x∈[-1,1]及a∈[-1,1]都成立,則t的取值范圍是
對所有的x∈[-1,1]及a∈[-1,1]都成立,則t的取值范圍是  _ .
_ .
【范例3】已知函數 與
與 的圖象相交于
的圖象相交于 ,
, ,
, ,
, 分別是
分別是 的圖象在
的圖象在 兩點的切線,
兩點的切線, 分別是
分別是 ,
, 與
與 軸的交點.
軸的交點.
(I)求 的取值范圍;
的取值范圍;
(II)設 為點
為點 的橫坐標,當
的橫坐標,當 時,寫出
時,寫出 以
以 為自變量的函數式,并求其定義域和值域;
為自變量的函數式,并求其定義域和值域;
(III)試比較 與
與 的大小,并說明理由(
的大小,并說明理由( 是坐標原點).
是坐標原點).
解:(I)由方程 消
消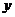 得
得 .????? ①
.????? ①
依題意,該方程有兩個正實根,
故 解得
解得 .
.
(II)由 ,求得切線
,求得切線 的方程為
的方程為 ,
,
由 ,并令
,并令 ,得
,得
 ,
, 是方程①的兩實根,且
是方程①的兩實根,且 ,故
,故 ,
, ,
,
 是關于
是關于 的減函數,所以
的減函數,所以 的取值范圍是
的取值范圍是 .
.
 是關于
是關于 的增函數,定義域為
的增函數,定義域為 ,所以值域為
,所以值域為 ,
,
(III)當 時,由(II)可知
時,由(II)可知 .
.
類似可得 .
. .
.
由①可知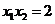 .
.
從而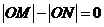 .
.
當 時,有相同的結果
時,有相同的結果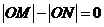 .
.
所以 .
.
變式:已知函數
 的最大值是
的最大值是 ,最小值是
,最小值是 ,求
,求 的值。
的值。
分析提示:(1)能化成關于 的二次函數,注意對數的運算法則;(2)注意挖掘隱含條件“
的二次函數,注意對數的運算法則;(2)注意挖掘隱含條件“ ”;(3)掌握復合函數最值問題的求解方法。
”;(3)掌握復合函數最值問題的求解方法。
解:

= , ∵
, ∵ ,且
,且
∴當 即
即 時,
時,
∴ ∴
∴ ,又
,又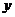 最大值是
最大值是 ,,
,,
∴ 即
即 , ∴
, ∴ 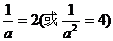 ∴
∴
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com