
【題目】將1,2,3,……,100這100個自然數,任意分為50組,每組兩個數,現將每組的兩個數中任一數值記作a,另一個記作b,代入代數式![]() 中進行計算,求出其結果,50組數代入后可求得50個值,則這50個值的和的最大值是___________
中進行計算,求出其結果,50組數代入后可求得50個值,則這50個值的和的最大值是___________
【答案】1275
【解析】①若a≥b,則代數式中絕對值符號可直接去掉,
∴代數式等于a,
②若b>a則絕對值內符號相反,
∴代數式等于b
由此可見輸入一對數字,可以得到這對數字中大的那個數(這跟誰是a誰是b無關)
既然是求和,那就要把這五十個數加起來還要最大,
我們可以枚舉幾組數,找找規律,
如果100和99一組,那么99就被浪費了,
因為輸入100和99這組數字,得到的只是100,
如果我們取兩組數字100和1一組,99和2一組,
則這兩組數字代入再求和是199,
如果我們這樣取100和99 2和1,
則這兩組數字代入再求和是102,
這樣,可以很明顯的看出,應避免大的數字和大的數字相遇這樣就可以使最后的和最大,
由此一來,只要100個自然數里面最大的五十個數字從51到100任意倆個數字不同組,
這樣最終求得五十個數之和最大值就是五十個數字從51到100的和,
51+52+53+…+100=3775.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖①,△ABC的角平分線BD,CE相交于點P.
(1)如果∠A=80,求∠BPC= .
(2)如圖②,過點P作直線MN∥BC,分別交AB和AC于點M和N,試求∠MPB+∠NPC的度數(用含∠A的代數式表示) .
(3)將直線MN繞點P旋轉。
(i)當直線MN與AB,AC的交點仍分別在線段AB和AC上時,如圖③,試探索∠MPB,∠NPC,∠A三者之間的數量關系,并說明你的理由。
(ii)當直線MN與AB的交點仍在線段AB上,而與AC的交點在AC的延長線上時,如圖④,試問(i)中∠MPB,∠NPC,∠A三者之間的數量關系是否仍然成立?若成立,請說明你的理由;若不成立,請給出∠MPB,∠NPC,∠A三者之間的數量關系,并說明你的理由。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,等邊三角形 ABC 的邊長為 3,過點 B 的直線 l⊥AB,且△ABC 與△A′BC′關于直線 l 對稱,D 為線段 BC′上一動點,則 AD+CD 的最小值是_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,拋物線c1:y=ax2﹣4a+4(a<0)經過第一象限內的定點P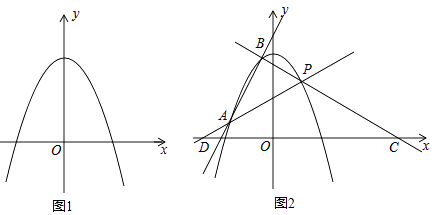
(1)直接寫出點P的坐標;
(2)若a=﹣1,如圖1,點M的坐標為(2,0)是x軸上的點,N為拋物線c1上的點,Q為線段MN的中點,設點N在拋物線c1上運動時,Q的運動軌跡為拋物線c2 , 求拋物線c2的解析式;
(3)直線y=2x+b與拋物線c1相交于A、B兩點,如圖2,直線PA、PB與x軸分別交于D、C兩代女.當PD=PC時,求a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】賽龍舟是端午節的主要習俗,某市甲乙兩支龍舟隊在端午節期間進行劃龍舟比賽,從起點A駛向終點B,在整個行程中,龍舟離開起點的距離y(米)與時間x(分鐘)的對應關系如圖所示,請結合圖象解答下列問題: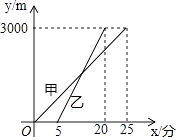
(1)起點A與終點B之間相距多遠?
(2)哪支龍舟隊先出發?哪支龍舟隊先到達終點?
(3)分別求甲、乙兩支龍舟隊的y與x函數關系式;
(4)甲龍舟隊出發多長時間時兩支龍舟隊相距200米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,AB=9,點E在CD邊上,且DE=2CE,點P是對角線AC上的一個動點,則PE+PD的最小值是( )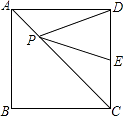
A.3 ![]()
B.10 ![]()
C.9
D.9 ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知點E、F在直線AB上,點G在線段CD上,ED與FG交于點H,∠C=∠EFG,∠CED=∠GHD.
(1)求證:CE∥GF;
(2)試判斷∠AED與∠D之間的數量關系,并說明理由;
(3)若∠EHF=100°,∠D=30°,求∠AEM的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一水果經銷商購進了A,B兩種水果各10箱,分配給他的甲、乙兩個零售店(分別簡稱甲店、乙店)銷售,預計每箱水果的盈利情況如下表:
A種水果/箱 | B種水果/箱 | |
甲店 | 11元 | 17元 |
乙店 | 9元 | 13元 |
(1)如果甲、乙兩店各配貨10箱,其中A種水果兩店各5箱,B種水果兩店各5箱,請你計算出經銷商能盈利多少元?
(2)在甲、乙兩店各配貨10箱(按整箱配送),且保證乙店盈利不小于100元的條件下,請你設計出使水果經銷商盈利最大的配貨方案,并求出最大盈利為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將一個含有45°角的直角三角板的直角頂點放在一張寬為2cm的矩形紙帶邊沿上,另一個頂點在紙帶的另一邊沿上.若測得三角板的一邊與紙帶的一邊所在的直線成30°角,則三角板最長邊的長是( )

A. 2cm B. 4cm C. 2![]() cm D. 4
cm D. 4![]() cm
cm
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com