
【題目】如圖,四邊形 ABCD 為矩形,點 E 為 BC 上的一點,滿足 AB CF BE CE ,連接 DE ,延長 EF交 AD 于 M 點,若 AE ![]() FD
FD ![]() AF
AF ![]() , DEF 15°,則M 的度數為_____.
, DEF 15°,則M 的度數為_____.
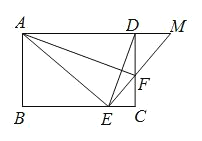
【答案】60°
【解析】
根據矩形的性質可得∠B=∠C=90°,AD∥BC,然后根據相似三角形的判定定理即可證出△ABE∽△ECF,從而得出∠AEB=∠EFC,然后求出∠AEF,結合勾股定理和已知條件即可證出EF=FD,根據等邊對等角可得∠DEF=∠EDF=15°,然后根據三角形外角的性質、平行線的性質即可求出結論.
解:∵四邊形 ABCD 為矩形,
∴∠B=∠C=90°,AD∥BC
∴∠EFC+∠FEC=90°
∵AB CF BE CE ,
∴![]()
∴△ABE∽△ECF
∴∠AEB=∠EFC
∴∠AEB+∠FEC=90°
∴∠AEF=180°-(∠AEB+∠FEC)=90°
在Rt△AEF中,AE![]() EF
EF![]() AF
AF![]() ,
,
∵AE![]() FD
FD![]() AF
AF![]() ,
,
∴EF=FD
∴∠DEF=∠EDF=15°
∴∠EFC=∠DEF+∠EDF=30°
∴∠FEC=90°-∠EFC=60°
∵AD∥BC
∴∠M=∠FEC=60°
故答案為:60°.


 暑假銜接教材期末暑假預習武漢出版社系列答案
暑假銜接教材期末暑假預習武漢出版社系列答案 假期作業暑假成長樂園新疆青少年出版社系列答案
假期作業暑假成長樂園新疆青少年出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖,△ABC與△CDE為等腰直角三角形,∠BAC=∠DEC=90°,連接AD,取AD中點P,連接BP,并延長到點M,使BP=PM,連接AM、EM、AE,將△CDE繞點C順時針旋轉.
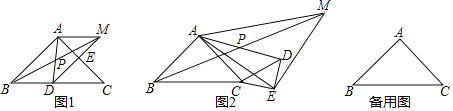
(1)如圖①,當點D在BC上,E在AC上時,AE與AM的數量關系是______,∠MAE=______;
(2)將△CDE繞點C順時針旋轉到如圖②所示的位置,(1)中的結論是否仍然成立,若成立,請給出證明,若不成立,請說明理由;
(3)若CD=![]() BC,將△CDE由圖①位置繞點C順時針旋轉α(0°<α<360°),當ME=
BC,將△CDE由圖①位置繞點C順時針旋轉α(0°<α<360°),當ME=![]() CD時,請直接寫出α的值.
CD時,請直接寫出α的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】鐘南山院士談到防護新型冠狀病毒肺炎時說:“我們需要重視防護,但也不必恐慌,盡量少去人員密集的場所,出門戴口罩,在室內注意通風,勤洗手,多運動,少熬夜.”某社區為了加強社區居民對新型冠狀病毒肺炎防護知識的了解,通過微信群宣傳新型冠狀病毒 肺炎的防護知識,并鼓勵社區居民在線參與作答《2020 年新型冠狀病毒防治全國統一考試 (全國卷)》試卷(滿分 100 分),社區管理員隨機從甲、乙兩個小區各抽取 20 名人員的 答卷成績,并對他們的成績(單位:分)進行統計、分析,過程如下:
收集數據
甲小區:85 80 95 100 90 95 85 65 75 85 90 90 70 90 100 80 80 90 95 75
乙小區:80 60 80 95 65 100 90 85 85 80 95 75 80 90 70 80 95 75 100 90
整理數據
60≤x≤70 | 70<x≤80 | 80<x≤90 | 90<x≤100 | |
甲小區 | 2 | 5 | 8 | 5 |
乙小區 | 3 | 7 | 5 | 5 |
分析數據
平均數 | 中位數 | 眾數 | |
甲小區 | 85.75 | 87.5 | a |
乙小區 | 83.5 | b | 80 |
應用數據
(1)填空:a = ,b =___,
(2)若甲小區共有 800 人參與答卷,請估計甲小區成績大于 90 分的人數為_____________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知圓O的直徑AB=12,點C是圓上一點,且∠ABC=30°,點P是弦BC上一動點,過點P作PD⊥OP交圓O于點D.

(1)如圖1,當PD∥AB 時,求PD的長;
(2)如圖2,當BP平分∠OPD時,求PC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為2的正方形![]() 中,點
中,點![]() 、
、![]() 分別是邊
分別是邊![]() 、
、![]() 上的兩個動點(與點
上的兩個動點(與點![]() 、
、![]() 、
、![]() 不重合),且始終保持
不重合),且始終保持![]() ,
,![]() ,
,![]() 交正方形外角平分線
交正方形外角平分線![]() 于點
于點![]() ,
,![]() 交
交![]() 于點
于點![]() ,連結
,連結![]() .
.
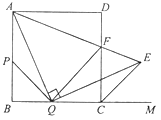
(1)求證:![]() ;
;
(2)證明:![]() ;
;
(3)設![]() ,當
,當![]() 為何值時,
為何值時,![]() ,并求出此時
,并求出此時![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形 ABCD 為正方形,取 AB 中點O ,以 AB 為直徑, O 圓心作圓.
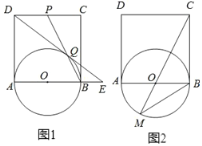
(1)如圖 1,取CD 的中點 P ,連接 BP 交⊙ O 于Q ,連接 DQ 并延長交 AB 的延長線于 E ,求證: QE ![]() BE AE ;
BE AE ;
(2)如圖 2,連接 CO 并延長交⊙ O 于 M 點,求tanM 的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】名聞遐邇的采花毛尖明前茶,成本每廳400元,某茶場今年春天試營銷,每周的銷售量y(斤)是銷售單價x(元/斤)的一次函數,且滿足如下關系:
x(元/斤) | 450 | 500 | 600 |
y(斤) | 350 | 300 | 200 |
(1)請根據表中的數據求出y與x之間的函數關系式;
(2)若銷售每斤茶葉獲利不能超過40%,該茶場每周獲利不少于30000元,試確定銷售單價x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某區對即將參加中考的5000名初中畢業生進行了一次視力抽樣調查,繪制出頻數分布表和頻數分布直方圖的一部分.請根據圖表信息回答下列問題:
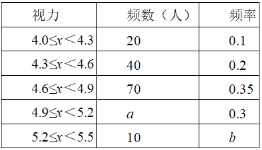
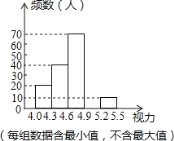
(1)本次調查的樣本為 ,樣本容量為 ;
(2)在頻數分布表中,a= ,b= ,并將頻數分布直方圖補充完整;
(3)若視力在4.6以上(含4.6)均屬正常,根據上述信息估計全區初中畢業生中視力正常的學生有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,拋物線![]() 與
與![]() 軸交于點
軸交于點![]() .
.
(1)試確定該拋物線的函數表達式;
(2)已知點![]() 是該拋物線的頂點,求
是該拋物線的頂點,求![]() 的面積;
的面積;
(3)若點![]() 是線段
是線段![]() 上的一動點,求
上的一動點,求![]() 的最小值.
的最小值.
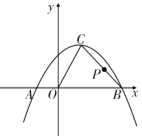
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com