
【題目】小雨、小華、小星暑假到某超市參加社會實踐活動,在活動中他們參加了某種水果的銷售工作,已知該水果的進價為8元![]() 千克.他們通過市場調查發現:當銷售單價為10元/千克時,那么每天可售出300千克;銷售單價每上漲1元,每天的銷售量就減少50千克.
千克.他們通過市場調查發現:當銷售單價為10元/千克時,那么每天可售出300千克;銷售單價每上漲1元,每天的銷售量就減少50千克.
(1)該超市銷售這種水果,當銷售單價不低于10元/千克時,請直接寫出每天的銷售量![]() (千克)與銷售單價
(千克)與銷售單價![]() (元
(元![]() 千克)之間的函數關系式;
千克)之間的函數關系式;
(2)一段時間后,發現這種水果每天的銷售量均不低于250千克,則此時該超市銷售這種水果每天獲取的利潤![]() (元
(元![]() 最大是多少?
最大是多少?
 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
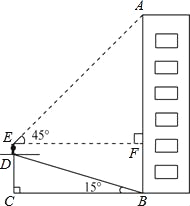
【題目】小華為了測量樓房AB的高度,他從樓底的B處沿著斜坡向上行走20m,到達坡頂D處.已知斜坡的坡角為15°.小華的身高ED是1.6m,他站在坡頂看樓頂A處的仰角為45°,求樓房AB的高度.(計算結果精確到1m)(參考數據:sin15°=![]() ,cos15°=
,cos15°=![]() ,tan15°=
,tan15°=![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
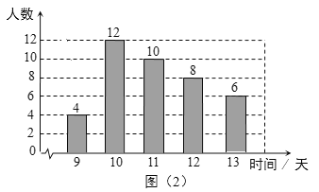
【題目】學校為了解全校學生參加社會實踐活動情況,隨機調查了部分學生一學期參加社會實踐活動的時間(單位:天),并用得到的數據繪制了統計圖(1)和圖 (2). 請根據圖中提供的信息,回答下列問題:

![]()
(1) 本次隨機調查的學生人數是_______,圖(1)中m的值是_______;
(2)求調查獲取的學生社會實踐活動時間樣本數據的眾數、中位數和平均數;
(3)該校有480名學生,根據獲取的社會實踐活動時間樣本數據,估計該校一學期社會實踐活動時間大于10 天的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
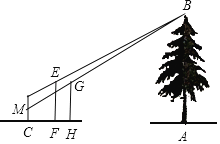
【題目】如圖,小華和小康想用標桿來測量河對岸的樹AB的高,兩人在確保無安全隱患的情況下,小康在F處豎立了一根標桿EF,小華走到C處時,站立在C處看到標桿頂端E和樹的頂端B在一條直線上,此時測得小華的眼睛到地面的距離DC=16米;然后,小華在C處蹲下,小康平移標桿到H處時,小華恰好看到標桿頂端G和樹的頂端B在一條直線上,此時測得小華的眼睛到地面的距離MC=0.8米.已知EF=GH=2.4米,CF=2米,FH=1.6米,點C、F、H、A在一條直線上,點M在CD上,CD⊥AC,EF⊥AC,CH⊥AC,AB⊥AC,根據以上測量過程及測量數據,請你求出樹AB的高度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校積極開展“陽光體育”活動,并開設了跳繩、足球、籃球、跑步四種運動項目,為了解學生最喜愛哪一種項目,隨機抽取了部分學生進行調查,并繪制了如下的條形統計圖和扇形統計圖(部分信息未給出).
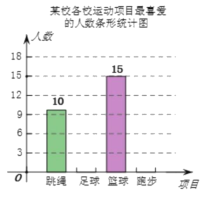
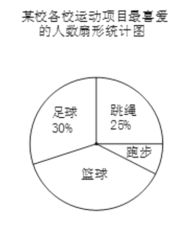
(1)求本次被調查的學生人數;
(2)補全條形統計圖;
(3)在扇形統計圖中,“籃球”部分所對應的圓心角度數為__ ;
(4)該校共有3000名學生,請估計全校最喜愛籃球的人數比最喜愛足球的人數多多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2020年由于受“疫情”影響,某廠只能按用戶的月需求量![]() (件)(
(件)(![]() )完成一種產品的生產,每件的售價為18萬元,每件的成本
)完成一種產品的生產,每件的售價為18萬元,每件的成本![]() (萬元),
(萬元),![]() 與
與![]() 的關系式為
的關系式為![]() (
(![]() ,
,![]() 為常數),經市場調研發現,月需求量
為常數),經市場調研發現,月需求量![]() 與月份
與月份![]() (
(![]() 為整數,
為整數,![]() )符合關系式
)符合關系式![]() (
(![]() 為常數),且得到下表中的數據.
為常數),且得到下表中的數據.

(1)求![]() 與
與![]() 滿足的關系式;
滿足的關系式;
(2)推斷哪個月產品的需求量最小?最小為多少件?
(3)在這一年12個月中,若![]() 個月和第(
個月和第(![]() )個月的利潤相差最大,求
)個月的利潤相差最大,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】受新型冠狀病毒疫情的影響,某市教育主管部門在推遲各級學校返校時間的同時安排各個學校開展形式多樣的網絡教學,學校計劃在每周三下午15:30至16:30為學生提供以下四類學習方式供學生選擇:在線閱讀、微課學習、線上答疑、在線討論,為了解學生的需求,通過網絡對部分學生進行了“你對哪類在線學習方式最感興趣”的調查,并根據調查結果繪制成如下兩幅不完整的統計圖.
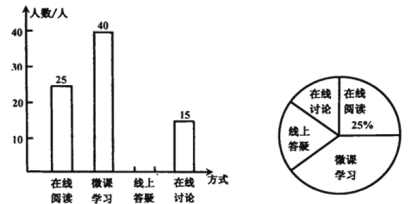
(1)求本次調查的學生總人數;
(2)請求出“線上答疑”在扇形統計圖中的圓心角度數;
(3)笑笑和瑞瑞同時參加了網絡學習,請求出笑笑和瑞瑞選擇同一種學習方式的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某游樂園有一個直徑為16米的圓形噴水池,噴水池的周邊有一圈噴水頭,噴出的水柱為拋物線,在距水池中心3米處達到最高,高度為5米,且各方向噴出的水柱恰好在噴水池中心的裝飾物處匯合.如圖所示,以水平方向為x軸,噴水池中心為原點建立直角坐標系.
(1)求水柱所在拋物線(第一象限部分)的函數表達式;
(2)王師傅在噴水池內維修設備期間,噴水管意外噴水,為了不被淋濕,身高1.8米的王師傅站立時必須在離水池中心多少米以內?
(3)經檢修評估,游樂園決定對噴水設施做如下設計改進:在噴出水柱的形狀不變的前提下,把水池的直徑擴大到32米,各方向噴出的水柱仍在噴水池中心保留的原裝飾物(高度不變)處匯合,請探究擴建改造后噴水池水柱的最大高度.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com