
廣東省汕頭市東里中學2008―2009年第二學期第一次考試高三數學(理科)
第一部分 選擇題(共40分)
一、選擇題:本大題共8小題,每小題5分,共40分.在每小題給出的四個選項中,只有一項是符合題目要求的.
1.設集合A=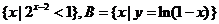 ,則
,則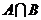 為
為
A.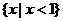 B.
B.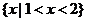 C.
C.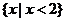 D.
D.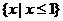
2.兩個圓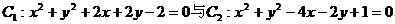 的公切線有且僅有:
的公切線有且僅有:
(A)1條 (B)2條 (C)3條 (D)4條
3.如圖是一個空間幾何體的主視圖、左視圖、俯視圖,已知主視圖、左視圖所對應的三角形皆為邊長為2的正三角形,俯視圖對應的四邊形為正方形,那么這個幾何體的表面積為:
A.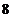 B.
B.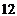 C.
C.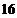 D.
D.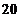

4.曲線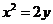 關于直線
關于直線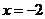 對稱的曲線方程是:
對稱的曲線方程是:
A. 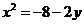 B.
B. 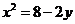 C.
C. 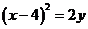 D.
D. 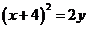
5.已知向量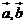 的夾角為
的夾角為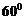 ,且
,且 在
在 中,
中,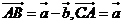 ,則角
,則角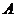 的值是:
的值是:
A. 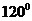 B.
B.
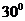 C.
C. 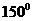 D.
D. 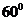
6.8.一個算法的程序框圖如下圖所示,若該程序輸出的結果為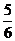 ,則判斷框中應填入的條件是
,則判斷框中應填入的條件是

A. 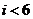 B.
B.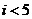 C.
C. 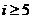 D.
D. 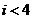
7.定義在 上的函數
上的函數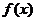 滿足
滿足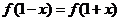 ,則“
,則“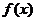 為偶函數”是“2為函數
為偶函數”是“2為函數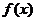 的一個周期”的( )條件
的一個周期”的( )條件
A.充分不必要 B.必要不充分 C.充要 D.既不充分有不必要
8.已知雙曲線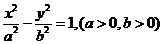 的左,右焦點分別為
的左,右焦點分別為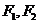 ,點P在雙曲線的右支上,且
,點P在雙曲線的右支上,且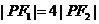 ,則此雙曲線的離心率e的最大值為
,則此雙曲線的離心率e的最大值為
(A)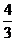 (B)
(B)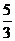 (C)
(C)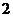 (D)
(D)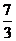
第二部分 非選擇題(共110分)
二、填空題:本大題共7小題,其中9~12題是必做題,13~15題是選做題. 每小題5分,滿分30分.
9.已知等差數列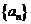 的前三項依次為1,
的前三項依次為1,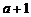 ,
,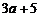 則數列
則數列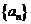 的通項公式是
的通項公式是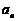 =__________.
=__________.
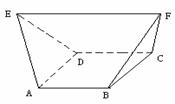
10.若復數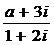 (
(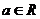 ,
,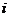 為虛數單位)是純虛數,則實數
為虛數單位)是純虛數,則實數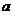 的值為
的值為
 11.在約束條件
11.在約束條件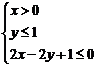 下,目標函數
下,目標函數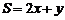 的最大值為_________.
的最大值為_________.
12.如圖,在多面體ABCDEF中,已知ABCD是邊長為1的正方形,且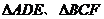 均為正三角形,EF∥AB,EF=2,則該多面體的體積為
均為正三角形,EF∥AB,EF=2,則該多面體的體積為
▲選做題:在下面三道小題中選做兩題,三題都選的只計算前兩題的得分.
13.(坐標系與參數方程選做題) 已知圓的極坐標方程為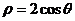 ,則該圓的圓心到直線
,則該圓的圓心到直線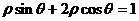 的距離是
.
的距離是
.
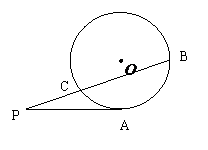 14.(不等式選講選做題)已知函數
14.(不等式選講選做題)已知函數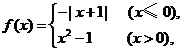 那么不等式
那么不等式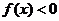 的解集為
.
的解集為
.
15.(幾何證明選講選做題) 如圖:PA與圓O相切于A,
PCB為圓O的割線,并且不過圓心O,已知 ∠BPA=
∠BPA=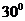 ,
,
PA=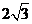 ,PC=1,則圓O的半徑等于
.
,PC=1,則圓O的半徑等于
.
三、解答題:本大題共6小題,共80分.解答應寫出文字說明、演算步驟或推證過程.
16.(本小題滿分12分)在△ABC中,角A、B、C的對邊分別為a、b、c.已知a+b=5,c =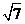 ,且
,且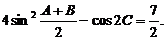
(1) 求角C的大小; (2)求△ABC的面積.
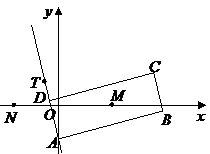 17.(本小題共14分)如圖,矩形
17.(本小題共14分)如圖,矩形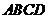 的兩條對角線相交于點
的兩條對角線相交于點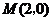 ,
,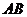 邊所在直線的方程為
邊所在直線的方程為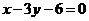 點
點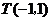 在
在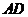 邊所在直線上.
邊所在直線上.
18.(本小題滿分12分)
四棱錐V-ABCD中,底面ABCD是正方形,側面VAD是正三角形,平面VAD⊥底面ABCD
1)求證AB⊥面VAD;
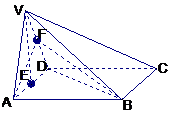 2)求面VAD與面VDB所成的二面角的大小.
2)求面VAD與面VDB所成的二面角的大小.
19.(本小題滿分12分)設A、B是雙曲線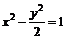 上的兩點,點N(1,2)是線段AB的中點.
上的兩點,點N(1,2)是線段AB的中點.
(I)求直線AB的方程
(II)如果線段AB的垂直平分線與雙曲線相交于C、D兩點,那么A、B、C、D四點是否共圓?為什么?
20.(本小題滿分12分)
已知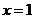 是函數
是函數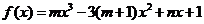 的一個極值點,其中
的一個極值點,其中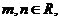
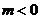 .
.
(Ⅰ)求m與n的關系表達式;
(Ⅱ)求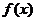 的單調區間;
的單調區間;
(Ⅲ)當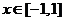 時,函數
時,函數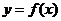 的圖象上任意一點的切線斜率恒大于3m,求m的取值范圍
的圖象上任意一點的切線斜率恒大于3m,求m的取值范圍
21.(本小題滿分14分) 已知數列{an}滿足a1=5,a2=5,an+1=an+6an-1(n≥2).
(1)求證:{an+1+2an}是等比數列;
(2)求數列{an}的通項公式;
(3)設3nbn=n(3n-an),且|b1|+|b2|+…+|bn|<m對于n∈N*恒成立,求m的取值范圍.
 東里中學2008―2009第二學期第一次考試
東里中學2008―2009第二學期第一次考試
數學答題卡(理科)
注意事項:⒈ 答題卷共4頁,用鋼筆或黑色(藍色)簽字筆直接答在試題卷中。
⒉ 答卷前將密封線內的項目填寫清楚。
題號
一
二
三
總分
16
17
18
19
20
21
分數
1 2 3 4
[A] [B] [C] [D] [A] [B] [C] [D] [A] [B] [C] [D] [A] [B] [C] [D]
5 6 7 8
[A] [B] [C] [D] [A] [B] [C] [D] [A] [B] [C] [D] [A] [B] [C] [D]
二、填空題:本大題共4小題,每小題5分,共20分。把最簡答案填在題中橫線上。
9.______ 10.____ 11. ________ 12.
三選二:13.__ 14. 15.
17(本小題滿分14分)
 三、解答題:6小題,共80分.解答應寫出文字說明,證明過程演算步驟。
三、解答題:6小題,共80分.解答應寫出文字說明,證明過程演算步驟。
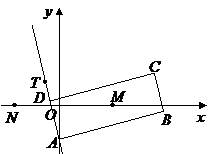
18(本小題滿分12分)

 19(本小題滿分14分)
19(本小題滿分14分)
 20(本小題滿分14分)
20(本小題滿分14分)
21(本小題滿分14分)
汕頭市東里中學2008―2009年第二學期第一次考試
二、填空題:
9. _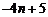 _ 10. -6 11.2 12.
_ 10. -6 11.2 12.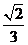 13.
13.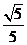 14.
14. 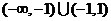 15.7
15.7
解析: 由圓的性質PA
由圓的性質PA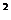 =PC?PB,得,PB=12,連接OA并反向延長交圓于點E,在直角三角形APD中可以求得PD=4,DA=2,故CD=3,DB=8,J記圓的半徑為R,由于ED?DA=CD?DB因此,(2R-2) ?2=3?8,解得R=7
=PC?PB,得,PB=12,連接OA并反向延長交圓于點E,在直角三角形APD中可以求得PD=4,DA=2,故CD=3,DB=8,J記圓的半徑為R,由于ED?DA=CD?DB因此,(2R-2) ?2=3?8,解得R=7
三、解答題:
16. (1) 解:∵A+B+C=180° 由
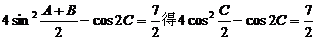 …………1分
…………1分
∴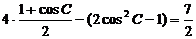 ………………3分
………………3分
整理,得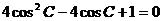 …………4分 解 得:
…………4分 解 得: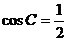 ……5分
……5分
∵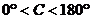 ∴C=60° ………………6分
∴C=60° ………………6分
(2)解:由余弦定理得:c2=a2+b2-2abcosC,即7=a2+b2-ab …………7分
∴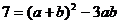 ………………8分 由條件a+b=5得 7=25-3ab …… 9分
………………8分 由條件a+b=5得 7=25-3ab …… 9分
 ……10分∴
……10分∴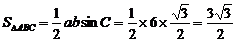 …………12分
…………12分
17.解:(I)因為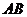 邊所在直線的方程為
邊所在直線的方程為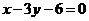 ,且
,且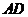 與
與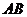 垂直,
垂直,
所以直線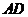 的斜率為
的斜率為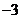 .……(2分)又因為點
.……(2分)又因為點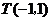 在直線
在直線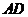 上,
上,
所以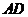 邊所在直線的方程為
邊所在直線的方程為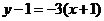 .即
.即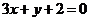 .…………(4分)
.…………(4分)
(II)由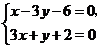 解得點
解得點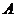 的坐標為
的坐標為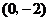 ,…………(6分)
,…………(6分)
因為矩形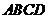 兩條對角線的交點為
兩條對角線的交點為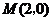 .所以
.所以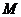 為矩形
為矩形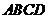 外接圓的圓心.
外接圓的圓心.
又半徑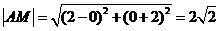 .矩形
.矩形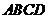 外接圓的方程為
外接圓的方程為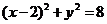 .……(9分)
.……(9分)
(III)因為動圓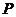 過點
過點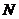 ,所以
,所以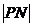 是該圓的半徑,又因為動圓
是該圓的半徑,又因為動圓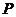 與圓
與圓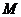 外切,
外切,
所以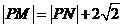 ,即
,即 .………………(11分)
.………………(11分)
故點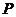 的軌跡是以
的軌跡是以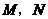 為焦點,實軸長為
為焦點,實軸長為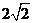 的雙曲線的左支.
的雙曲線的左支.
因為實半軸長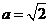 ,半焦距
,半焦距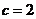 .所以虛半軸長
.所以虛半軸長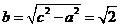 .
.
從而動圓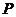 的圓心的軌跡方程為
的圓心的軌跡方程為 .………………(14分)
.………………(14分)
18.證法一:(1)由于面VAD是正三角形,設AD的中點為E,則VE⊥AD,…………(1分)
而面VAD⊥底面ABCD,而面VAD 底面ABCD
底面ABCD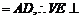 平面
平面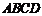 ,則VE⊥AB
,則VE⊥AB …………(4分)
…………(4分)
ABCD是正方形,則AB⊥AD,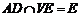 故AB⊥面VAD
故AB⊥面VAD ……(6分)
……(6分)
證明二:(Ⅰ)作AD的中點O,則VO⊥底面ABCD.…………1分
建立如圖空間直角坐標系,并設正方形邊長為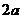 ,………2分
,………2分
則A( ,0,0),B(
,0,0),B( ,1,0),C(-
,1,0),C(- ,1,0),D(-
,1,0),D(- ,0,0),V(0,0,
,0,0),V(0,0,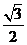 ),
),
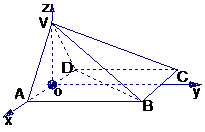 ∴
∴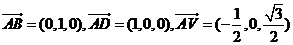 ……3分
……3分
由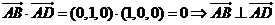 …………4分
…………4分
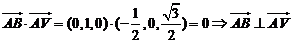 ……5分
……5分
又AB∩AV=A ∴AB⊥平面VAD…………………………6分
(Ⅱ)由(Ⅰ)得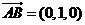 是面VAD的法向量……………………7分
是面VAD的法向量……………………7分
設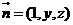 是面VDB的法向量,則
是面VDB的法向量,則
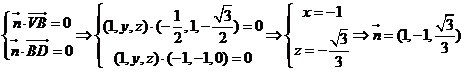 ……9分
……9分
∴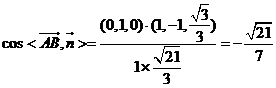 ,……………11分
,……………11分
又由題意知,面VAD與面VDB所成的二面角,所以其大小為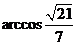 ……12分
……12分
19.解:(I)依題意,可設直線AB的方程為 y=k(x-1)+2,
代入 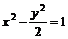 ,整理得
,整理得
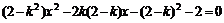 ①
①
記A(x1,y1),B(x2,y2),x1,x2則是方程①的兩個不同的根,所以2-k2≠0,且
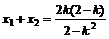 ,
,
由N(1,2)是AB的中點得
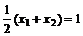 ,
,
∴ k(2-k)=2-k2,
解得k=1,所以直線AB的方程為
y=x+1
(II)將k=1代入方程①得x2-2x-3=0
解出 x1=-1,x2=3
由 y=x+1得 y1=0,y2=4。
即A、B的坐標分別為(-1,0)和(3,4)。
由CD垂直平分AB,得直線CD的方程為
y=-(x-1)+2,
即 y=3-x。
代入雙曲線方程,整理得 x2+6x-11=0。 ②
記C(x3,y3),D(x4,y4),以及CD的中點為M(x0,y0),則x3,x4是方程②的兩個根。所以x3+x4=-6,x3x4=-11。
從而 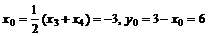
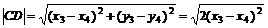
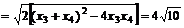
∴ 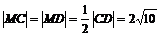
又 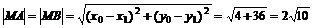
即A、B、C、D四點到點M的距離相等,所以A、B、C、D四點共圓。
20.
(Ⅰ)解: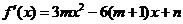 .
.
因為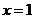 是
是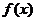 的一個極值點,所以
的一個極值點,所以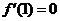 ,即
,即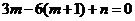 .
.
所以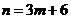

(Ⅱ)解:由(Ⅰ)知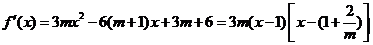
當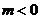 時,有
時,有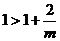 ,當
,當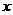 變化時
變化時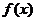 與
與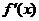 的變化如下表:
的變化如下表:
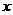
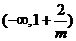
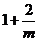
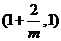
1
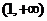
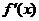
<0
0
>0
0
<0
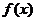
單調遞減
極小值
單調遞增
極大值
單調遞減
由上表知,當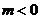 時,
時,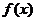 在
在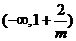 單調遞減,在
單調遞減,在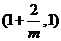 單調遞增, 在
單調遞增, 在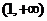 單調遞減
單調遞減
(Ⅲ)解法一:由已知,得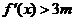 ,即
,即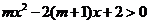 .
.

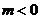 .
.
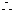
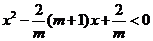 .
.
即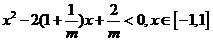 .
(*)
.
(*)
設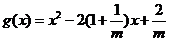 ,其函數圖象的開口向上.
,其函數圖象的開口向上.
由題意(*)式恒成立, 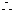
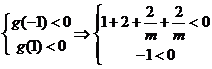
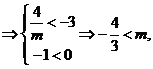 又
又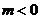 .
.
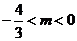
即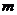 的取值范圍是
的取值范圍是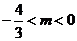

解法二:由已知,得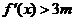 ,即
,即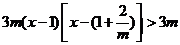 ,
,
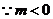 .
. 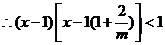 .
(*)
.
(*)
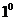
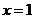 時. (*)式化為
時. (*)式化為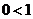 怛成立.
怛成立.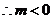 .
.

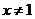 時
時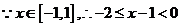 .
.
(*)式化為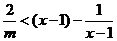 .
.
令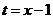 ,則
,則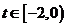 ,記
,記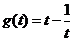 ,
,
則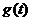 在區間
在區間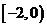 是單調增函數
是單調增函數
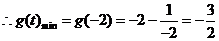 .
.
由(*)式恒成立,必有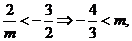 又
又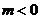 .
.
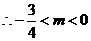 .
.
綜上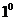 、
、 知
知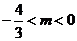

21.(本小題滿分14分) 已知數列{an}滿足a1=5,a2=5,an+1=an+6an-1(n≥2).
(1)求證:{an+1+2an}是等比數列;
(2)求數列{an}的通項公式;
(3)設3nbn=n(3n-an),且|b1|+|b2|+…+|bn|<m對于n∈N*恒成立,
求m的取值范圍.
20.(本小題滿分14分)
(1)由an+1=an+6an-1,an+1+2an=3(an+2an-1) (n≥2)
∵a1=5,a2=5 ∴a2+
故數列{an+1+2an}是以15為首項,3為公比的等比數列………………5分
(2)由(1)得an+1+2an=5?3n
由待定系數法可得(an+1-3n+1)=-2(an-3n)
即an-3n=2(-2)n-1
故an=3n+2(-2)n-1=3n-(-2)n…………………………………………10分
(3)由3nbn=n(3n-an)=n[3n-3n+(-2)n]=n(-2)n,∴bn=n(-)n
令Sn=|b1|+|b2|+…+|bn|=+2()2+3()3+…+n()n
Sn=()2+2()3+…+(n-1)()n+n()n+1
…………12分
得Sn=+()2+()3+…+()n-n()n+1
=-n()n+1=2[1-()n]-n()n+1
∴ Sn=6[1-()n]-3n()n+1<6
要使得|b1|+|b2|+…+|bn|<m對于n∈N*恒成立
只須m≥6………………………………………………………14分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com