
【題目】已知函數![]() .
.
(1)若關于![]() 的不等式
的不等式![]() 的解集是
的解集是![]() ,求
,求![]() ,
,![]() 的值;
的值;
(2)設關于![]() 的不等式
的不等式![]() 的解集是
的解集是![]() ,集合
,集合![]() ,若
,若![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1) ![]() ,
,![]() .
.
(2)![]() .
.
【解析】分析:(1)先根據不等式解集與對應方程根的關系得x2-(a+1)x+1=0的兩個實數根為m、2,再利用韋達定理得結果.(2)當A∩B=![]() 時,即不等式f(x)>0對x∈B恒成立,再利用變量分離法得a+1<x+
時,即不等式f(x)>0對x∈B恒成立,再利用變量分離法得a+1<x+![]() 的最小值,最后根據基本不等式求最值,即得結果.
的最小值,最后根據基本不等式求最值,即得結果.
詳解:(1)∵關于x的不等式f(x)<0的解集是{x|m<x<2},
∴對應方程x2-(a+1)x+1=0的兩個實數根為m、2,
由根與系數的關系,得![]() ,解得a=
,解得a=![]() ,m=
,m=![]() ;
;
(2)∵關于x的不等式f(x)≤0的解集是A,
集合B={x|0≤x≤1},當A∩B=![]() 時,即不等式f(x)>0對x∈B恒成立;
時,即不等式f(x)>0對x∈B恒成立;
即x∈![]() 時,x2-(a+1)x+1>0恒成立,
時,x2-(a+1)x+1>0恒成立,
∴a+1<x+![]() 對于x∈(0,1]恒成立(當
對于x∈(0,1]恒成立(當![]() 時,1>0恒成立);
時,1>0恒成立);
∵當x∈(0,1]時,![]()
∴a+1<2,即a<1,∴實數a的取值范圍是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】在正方體ABCD-A1B1C1D1中,下列說法正確的是____ (填序號).
(1)直線AC1在平面CC1B1B內.
(2)設正方形ABCD與A1B1C1D1的中心分別為O、O1,則平面AA1C1C與平面BB1D1D的交線為OO1.
(3)由A、C1、B1確定的平面是ADC1B1.
(4)由A、C1、B1確定的平面與由A、C1、D確定的平面是同一個平面.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P—ABCD中,△PAD為正三角形,平面PAD⊥平面ABCD,AB∥CD,AB⊥AD,CD=2AB=2AD=4.

(1)求證:平面PCD⊥平面PAD;
(2)求三棱錐P—ABC的體積;
(3)在棱PC上是否存在點E,使得BE∥平面PAD?若存在,
請確定點E的位置并證明;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() ,直線
,直線![]() 。
。
(Ⅰ)求證:直線![]() 與圓C恒有兩個交點;
與圓C恒有兩個交點;
(Ⅱ)求出直線![]() 被圓C截得的最短弦長,并求出截得最短弦長時的
被圓C截得的最短弦長,并求出截得最短弦長時的![]() 的值;
的值;
(Ⅲ)設直線![]() 與圓C的兩個交點為M,N,且
與圓C的兩個交點為M,N,且![]() (點C為圓C的圓心),求直線
(點C為圓C的圓心),求直線![]() 的方程。
的方程。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“一帶一路”是“絲綢之路經濟帶”和“21世紀海上絲綢之路”的簡稱.某市為了了解人們對“一帶一路”的認知程度,對不同年齡和不同職業的人舉辦了一次“一帶一路”知識競賽,滿分100分(90分及以上為認知程度高).現從參賽者中抽取了![]() 人,按年齡分成5組,第一組:
人,按年齡分成5組,第一組: ![]() ,第二組:
,第二組: ![]() ,第三組:
,第三組: ![]() ,第四組:
,第四組: ![]() ,第五組:
,第五組: ![]() ,得到如圖所示的頻率分布直方圖,已知第一組有6人.
,得到如圖所示的頻率分布直方圖,已知第一組有6人.
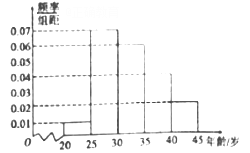
(1)求![]() ;
;
(2)求抽取的![]() 人的年齡的中位數(結果保留整數);
人的年齡的中位數(結果保留整數);
(3)從該市大學生、軍人、醫務人員、工人、個體戶 五種人中用分層抽樣的方法依次抽取6人,42人,36人,24人,12人,分別記為1~5組,從這5個按年齡分的組和5個按職業分的組中每組各選派1人參加知識競賽,分別代表相應組的成績,年齡組中1~5組的成績分別為93,96,97,94,90,職業組中1~5組的成績分別為93,98,94,95,90.
(Ⅰ)分別求5個年齡組和5個職業組成績的平均數和方差;
(Ⅱ)以上述數據為依據,評價5個年齡組和5個職業組對“一帶一路”的認知程度.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“![]() ”是“對任意的正數
”是“對任意的正數![]() ,
, ![]() ”的( )
”的( )
A. 充分不必要條件 B. 必要不充分條件 C. 充要條件 D. 既不充分也不必要條件
【答案】A
【解析】分析:根據基本不等式,我們可以判斷出“![]() ”?“對任意的正數x,2x+
”?“對任意的正數x,2x+![]() ≥1”與“對任意的正數x,2x+
≥1”與“對任意的正數x,2x+![]() ≥1”?“a=
≥1”?“a=
”真假,進而根據充要條件的定義,即可得到結論.
解答:解:當“a=![]() ”時,由基本不等式可得:
”時,由基本不等式可得:
“對任意的正數x,2x+![]() ≥1”一定成立,
≥1”一定成立,
即“a=![]() ”?“對任意的正數x,2x+
”?“對任意的正數x,2x+![]() ≥1”為真命題;
≥1”為真命題;
而“對任意的正數x,2x+![]() ≥1的”時,可得“a≥
≥1的”時,可得“a≥![]() ”
”
即“對任意的正數x,2x+![]() ≥1”?“a=
≥1”?“a=![]() ”為假命題;
”為假命題;
故“a=![]() ”是“對任意的正數x,2x+
”是“對任意的正數x,2x+![]() ≥1的”充分不必要條件
≥1的”充分不必要條件
故選A
【題型】單選題
【結束】
11
【題目】如圖,四棱錐![]() 中,
中, ![]() 平面
平面![]() ,底面
,底面![]() 為直角梯形,
為直角梯形, ![]() ,
, ![]()
![]() ,
, ![]() ,點
,點![]() 在棱
在棱![]() 上,且
上,且![]() ,則平面
,則平面![]() 與平面
與平面![]() 的夾角的余弦值為( )
的夾角的余弦值為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com