
【題目】已知函數![]()
![]() .
.
(1)若函數![]() 的圖象與直線
的圖象與直線![]() 沒有交點,求
沒有交點,求![]() 的取值范圍;
的取值范圍;
(2)設![]() ,若函數
,若函數![]() 與
與![]() 的圖象有且只有一個公共點,求實數
的圖象有且只有一個公共點,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)函數沒有交點,即方程沒有解,可得到方程![]() 無解,構造函數
無解,構造函數![]() ,求其值域,進而可求出
,求其值域,進而可求出![]() 的取值范圍;
的取值范圍;
(2)兩函數只有一個公共點,即方程![]() 只有一個解,結合對數的運算性質及二次函數的性質,分類討論可求出
只有一個解,結合對數的運算性質及二次函數的性質,分類討論可求出![]() 的取值范圍.
的取值范圍.
(1)由題意,方程![]() 無解,即方程
無解,即方程![]() 無解,
無解,
令![]() ,則函數
,則函數![]() 與
與![]() 的圖象無交點.
的圖象無交點.
![]() ,
,
令![]() ,因為
,因為![]() ,所以
,所以![]() ,
,
因為函數![]() 是
是![]() 上的增函數,所以
上的增函數,所以![]() 的值域是
的值域是![]() ,即函數
,即函數![]() 的值域為
的值域為![]() .
.
故只需![]() ,可使函數
,可使函數![]() 與
與![]() 的圖象無交點.
的圖象無交點.
即![]() 的取值范圍是
的取值范圍是![]() .
.
(2)由題意,方程![]() 只有一個解,
只有一個解,
![]() ,
,
即方程為![]() ,
,
則方程![]() 只有一個解,
只有一個解,
令![]() ,則
,則![]() ,整理得
,整理得![]() ,該方程有且僅有一個正解.
,該方程有且僅有一個正解.
①當![]() 時,則
時,則![]() ,解得
,解得![]() ,不符合題意,舍去;
,不符合題意,舍去;
②當![]() 時,則
時,則![]() 為開口向上的二次函數,當
為開口向上的二次函數,當![]() 時,
時,![]() ,
,
顯然,二次函數![]() 存在唯一正零點,即方程
存在唯一正零點,即方程![]() 有且僅有一個正解,符合題意;
有且僅有一個正解,符合題意;
③當![]() 時,則
時,則![]() 為開口向下的二次函數.
為開口向下的二次函數.
若一元二次方程![]() 有兩個相同正解,則
有兩個相同正解,則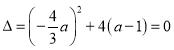 ,解得
,解得![]() 或
或![]() .
.
![]() 時,解得
時,解得![]() ,不合題意,舍去;
,不合題意,舍去;![]() 時,解得
時,解得![]() ,符合題意;
,符合題意;
若一元二次方程![]() 有兩個不同的解,且只有一個正解,則
有兩個不同的解,且只有一個正解,則![]() ,解得
,解得![]() 或
或![]() ,且
,且![]() ,即
,即![]() ,不符合
,不符合![]() ,舍去.
,舍去.
綜上,![]() 的取值范圍是
的取值范圍是![]() 或
或![]() .
.


 輕松課堂單元期中期末專題沖刺100分系列答案
輕松課堂單元期中期末專題沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() ;
;
(1)當![]() 時,若
時,若![]() ,求
,求![]() 的取值范圍;
的取值范圍;
(2)若定義在![]() 上奇函數
上奇函數![]() 滿足
滿足![]() ,且當
,且當![]() 時,
時, ![]() ,
,
求![]() 在
在![]() 上的反函數
上的反函數![]() ;
;
(3)對于(2)中的![]() ,若關于
,若關于![]() 的不等式
的不等式 在
在![]() 上恒成立,求實
上恒成立,求實
數![]() 的取值范圍;
的取值范圍;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 上一動點
上一動點![]() ,過點
,過點![]() 作
作![]() 軸,垂足為
軸,垂足為![]() 點,
點,![]() 中點為
中點為![]() .
.
(1)當![]() 在圓
在圓![]() 上運動時,求點
上運動時,求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)過點![]() 的直線
的直線![]() 與
與![]() 交于
交于![]() 兩點,當
兩點,當![]() 時,求線段
時,求線段![]() 的垂直平分線方程.
的垂直平分線方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,設拋物線![]() 的準線
的準線![]() 與
與![]() 軸交于橢圓
軸交于橢圓![]() 的右焦點
的右焦點![]() 為
為![]() 的左焦點.橢圓的離心率為
的左焦點.橢圓的離心率為![]() ,拋物線
,拋物線![]() 與橢圓
與橢圓![]() 交于
交于![]() 軸上方一點
軸上方一點![]() ,連接
,連接![]() 并延長其交
并延長其交![]() 于點
于點![]() ,
, ![]() 為
為![]() 上一動點,且在
上一動點,且在![]() 之間移動.
之間移動.
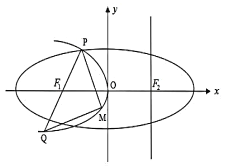
(1)當![]() 取最小值時,求
取最小值時,求![]() 和
和![]() 的方程;
的方程;
(2)若![]() 的邊長恰好是三個連續的自然數,當
的邊長恰好是三個連續的自然數,當![]() 面積取最大值時,求面積最大值以及此時直線
面積取最大值時,求面積最大值以及此時直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】填空:
(1)如果![]() ,且
,且![]() ,則
,則![]() 是第________象限角;
是第________象限角;
(2)如果![]() ,且
,且![]() ,則
,則![]() 是第________象限角;
是第________象限角;
(3)如果![]() ,且
,且![]() ,則
,則![]() 是第________象限角;
是第________象限角;
(4)如果![]() ,且
,且![]() ,則
,則![]() 是第________象限角.
是第________象限角.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了發展電信事業方便用戶,電信公司對移動電話采用不同的收費方式,其中所使用的“如意卡”與“便民卡”在某市范圍內每月(30天)的通話時間x(分)與通話費y(元)的關系分別如圖①、②所示.

(1)分別求出通話費y1,y2與通話時間x之間的函數關系式;
(2)請幫助用戶計算,在一個月內使用哪種卡便宜?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,由均勻材質制成的一個正20面體(每個面都是正三角形),將20個面平分成10組,第1組標上0,第2組標上1,…,第10組標上9.
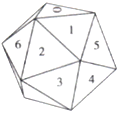
(1)投擲正20面體,若把朝上一面的數字作為投擲結果,則出現0,1,2,…,9是等可能的嗎?
(2)三個正20面體分別涂上紅、黃、藍三種顏色,分別代表百位、十位、個位,同時投擲可以產生一個三位數(百位為0的也看作三位數),它是000~999范圍內的隨機數嗎?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】使用支付寶和微信支付已經成為廣大消費者最主要的消費支付方式,某超市通過統計發現一周內超市每天的凈利潤![]() (萬元)與每天使用支付寶和微信支付的人數
(萬元)與每天使用支付寶和微信支付的人數![]() (千人)具有相關關系,并得到最近一周
(千人)具有相關關系,并得到最近一周![]() 的7組數據如下表,并依此作為決策依據.
的7組數據如下表,并依此作為決策依據.
周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
13 | 16 | 26 | 22 | 25 | 29 | 30 |
7 | 11 | 15 | 22 | 24 | 27 | 34 |
(Ⅰ)作出散點圖,判斷![]() 與
與![]() 哪一個適合作為每天凈利潤的回歸方程類型?并求出回歸方程(
哪一個適合作為每天凈利潤的回歸方程類型?并求出回歸方程(![]() ,
,![]() ,
,![]() ,
,![]() 精確到
精確到![]() );
);

(Ⅱ)超市為了刺激周一消費,擬在周一開展使用支付寶和微信支付隨機抽獎活動,總獎金7萬元.根據市場調查,抽獎活動能使使用支付寶和微信支付消費人數增加6千人,7千人,8千人,9千人的概率依次為![]() ,
,![]() ,
,![]() ,
,![]() .試決策超市是否有必要開展抽獎活動?
.試決策超市是否有必要開展抽獎活動?
參考數據: ![]() ,
,![]() ,
,![]() ,
,![]() .
.
參考公式:![]() ,
, ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com