
【題目】如圖所示,線段![]() 是⊙
是⊙![]() 的直徑,過
的直徑,過![]() 點作直線
點作直線![]() 交⊙
交⊙![]() 于
于![]() 、
、![]() 兩點,過
兩點,過![]() 點作
點作![]() 的角平分線交⊙
的角平分線交⊙![]() 于
于![]() ,過
,過![]() 作
作![]() 的垂線交
的垂線交![]() 于
于![]()
(1)證明![]() 是⊙
是⊙![]() 的切線
的切線
(2)證明![]()
(3)若⊙![]() 的直徑為10,
的直徑為10,![]() ,求
,求![]()
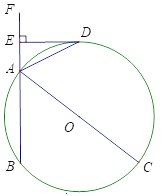
【答案】(1)證明見解析;(2)證明見解析;(3)8.
【解析】
(1)連接OD,由∠ADE+∠DAE=90°,![]() =
=![]() =∠ODA,即可證明∠ODE=90°.
=∠ODA,即可證明∠ODE=90°.
(2)連接CD,根據已知條件證明![]() ∽
∽![]() 即可求解;
即可求解;
(3)過點O作OM⊥AB于點M,則四邊形ODEM為矩形,設DE=OM=x,則AE=4-x,![]() 利用在
利用在![]() 中,
中,![]() ,列出方程求解x,再利用垂徑定理即可求解.
,列出方程求解x,再利用垂徑定理即可求解.
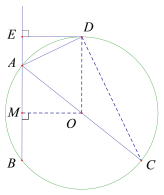
(1)證明:連接OD
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
又∵![]()
∴![]()
![]() 為⊙O切線
為⊙O切線
(2)解:連接CD
∵![]() 為⊙O的直徑,DE⊥AF
為⊙O的直徑,DE⊥AF
∴![]() ADC=90°,∠DEA=90°,
ADC=90°,∠DEA=90°,
∴∠ADC=∠AED
∴在![]() 和
和![]() 中
中![]()
∴![]() ∽
∽![]()
∴![]()
∴![]()
∵![]()
∴![]()
(3)過點O作OM⊥AB于點M,則四邊形ODEM為矩形,
設DE=OM=x,則AE=4-x,
∴![]()
在![]() 中,
中,![]() ,
,
即:![]()
解得:![]() (舍去)
(舍去)
∴![]()
∵![]() 由垂徑定理得:AB=2AM=8
由垂徑定理得:AB=2AM=8


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
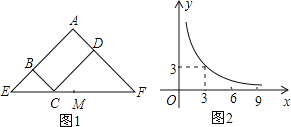
【題目】如圖1所示矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 與
與![]() 滿足的反比例函數關系如圖2所示,等腰直角三角形
滿足的反比例函數關系如圖2所示,等腰直角三角形![]() 的斜邊
的斜邊![]() 過
過![]() 點,點
點,點![]() ,
,![]() 分別在
分別在![]() ,
,![]() 上,
上,![]() 為
為![]() 的中點,則下列結論正確的是( )
的中點,則下列結論正確的是( )
A.當![]() 時,
時,![]()
B.當![]() 時,
時,![]()
C.當![]() 增大時,
增大時,![]() 的值增大
的值增大
D.當![]() 增大時,
增大時,![]() 的值不變
的值不變
查看答案和解析>>
科目:初中數學 來源: 題型:
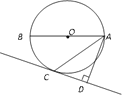
【題目】如圖,已知AB是⊙O的直徑,AC為弦,且平分∠BAD,AD⊥CD,垂足為D.
(1) 求證:CD是⊙O的切線;
(2) 若⊙O的直徑為4,AD=3,試求∠BAC的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
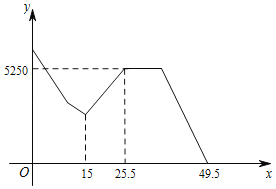
【題目】甲、乙兩人同時騎自行車分別從A、B兩地出發到AB之間的C地,且A、B、C三地在同一直線上.當乙到達C地時甲還未到達,乙在C地等了5分鐘,接到甲的電話說他的自行車壞了需要工具修理,于是乙在C地拿了工具箱立即以原來![]() 倍的速度前往甲壞車處,乙與甲會合后幫助甲花了10分鐘修好自行車,然后兩人以甲原來
倍的速度前往甲壞車處,乙與甲會合后幫助甲花了10分鐘修好自行車,然后兩人以甲原來![]() 倍的速度騎行同時到達C地.甲乙兩人距C地的距離之和y(米)與甲所用時間x(分鐘)之間的函數關系如圖所示(乙接電話和找工具箱的時間忽略不計),則A、B兩地之間的距離為___米.
倍的速度騎行同時到達C地.甲乙兩人距C地的距離之和y(米)與甲所用時間x(分鐘)之間的函數關系如圖所示(乙接電話和找工具箱的時間忽略不計),則A、B兩地之間的距離為___米.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在平面直角坐標系中,拋物線y=![]() 與x軸交于A、B兩點(點A在點B的左側),與y軸交于點C.
與x軸交于A、B兩點(點A在點B的左側),與y軸交于點C.
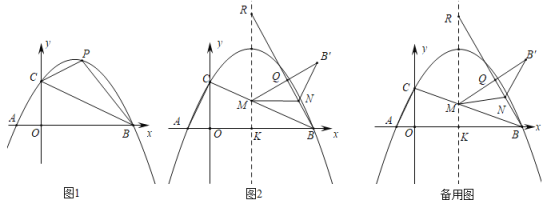
(1)點P為線段BC上方拋物線上(不與B、C重合)的一動點,連接PC、PB,當△PBC面積最大時,在y軸找點D,使得PD﹣![]() OD的值最小時,求這個最小值.
OD的值最小時,求這個最小值.
(2)如圖2,拋物線對稱軸與x軸交于點K,與線段BC交于點M,在對稱軸上取一點R,使得KR=12(點R在第一象限),連接BR.已知點N為線段BR上一動點,連接MN,將△BMN沿MN翻折到△B'MN.當△B'MN與△BMR重疊部分(如圖中的△MNQ)為直角三角形時,直接寫出此時點B'的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
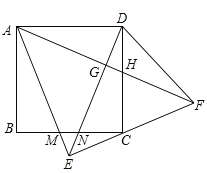
【題目】如圖,正方形ABCD中,以AD為底邊作等腰△ADE,將△ADE沿DE折疊,點A落到點F處,連接EF剛好經過點C,再連接AF,分別交DE于點G,交CD于點H,下列結論:①△ABM≌△DCN;②∠DAF=30°;③△AEF是等腰直角三角形;④EC=CF;⑤![]() ,其中正確的有__________.
,其中正確的有__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD中,M為BC上一點,ME⊥AM,ME交CD于點F,交AD的延長線于點E,若AB=4,BM=2,則△DEF的面積為( )

A.9B.8C.15D.14.5
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com