
【題目】如圖1,拋物線(xiàn)W:y=ax2﹣2的頂點(diǎn)為點(diǎn)A,與x軸的負(fù)半軸交于點(diǎn)D,直線(xiàn)AB交拋物線(xiàn)W于另一點(diǎn)C,點(diǎn)B的坐標(biāo)為(1,0).
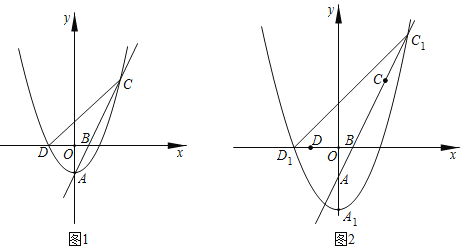
(1)求直線(xiàn)AB的解析式;
(2)過(guò)點(diǎn)C作CE⊥x軸,交x軸于點(diǎn)E,若AC平分∠DCE,求拋物線(xiàn)W的解析式;
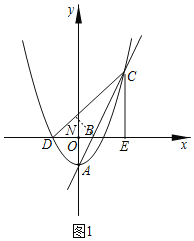
(3)若a=![]() ,將拋物線(xiàn)W向下平移m(m>0)個(gè)單位得到拋物線(xiàn)W1,如圖2,記拋物線(xiàn)W1的頂點(diǎn)為A1,與x軸負(fù)半軸的交點(diǎn)為D1,與射線(xiàn)BC的交點(diǎn)為C1.問(wèn):在平移的過(guò)程中,tan∠D1C1B是否恒為定值?若是,請(qǐng)求出tan∠D1C1B的值;若不是,請(qǐng)說(shuō)明理由.
,將拋物線(xiàn)W向下平移m(m>0)個(gè)單位得到拋物線(xiàn)W1,如圖2,記拋物線(xiàn)W1的頂點(diǎn)為A1,與x軸負(fù)半軸的交點(diǎn)為D1,與射線(xiàn)BC的交點(diǎn)為C1.問(wèn):在平移的過(guò)程中,tan∠D1C1B是否恒為定值?若是,請(qǐng)求出tan∠D1C1B的值;若不是,請(qǐng)說(shuō)明理由.
【答案】(1)y=2x﹣2;(2)y=![]() x2﹣2;(3)tan∠D1C1B恒為定值,
x2﹣2;(3)tan∠D1C1B恒為定值,![]() ,見(jiàn)解析
,見(jiàn)解析
【解析】
(1)由待定系數(shù)法可求解析式;
(2)如圖1,過(guò)點(diǎn)![]() 作
作![]() 于
于![]() ,通過(guò)證明
,通過(guò)證明![]() ,可得
,可得![]() ,由平行線(xiàn)分線(xiàn)段成比例可求
,由平行線(xiàn)分線(xiàn)段成比例可求![]() ,可得
,可得![]() ,
,![]() ,設(shè)
,設(shè)![]() ,
,![]() ,則
,則![]() ,
,![]() ,由勾股定理可求
,由勾股定理可求![]() ,可求點(diǎn)
,可求點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 坐標(biāo),代入解析式可求
坐標(biāo),代入解析式可求![]() 的值,即可求拋物線(xiàn)
的值,即可求拋物線(xiàn)![]() 的解析式;
的解析式;
(3)先求出點(diǎn)![]() 的坐標(biāo)
的坐標(biāo)![]() ,如圖2,過(guò)點(diǎn)
,如圖2,過(guò)點(diǎn)![]() 作
作![]() 軸,過(guò)點(diǎn)
軸,過(guò)點(diǎn)![]() 作
作![]() 軸,可證
軸,可證![]() ,可得
,可得![]() ,如圖3,過(guò)點(diǎn)
,如圖3,過(guò)點(diǎn)![]() 作
作![]() 于點(diǎn)
于點(diǎn)![]() ,由勾股定理和直角三角形的性質(zhì)可求
,由勾股定理和直角三角形的性質(zhì)可求![]() ,
,![]() ,
,![]() 的長(zhǎng),即可求
的長(zhǎng),即可求![]() .
.
解:(1)∵拋物線(xiàn)W:y=ax2﹣2的頂點(diǎn)為點(diǎn)A,
∴點(diǎn)A(0,﹣2)
設(shè)直線(xiàn)AB解析式為y=kx+b,
∴![]()
解得![]()
∴拋物線(xiàn)解析式為:y=2x﹣2;
(2)如圖1,過(guò)點(diǎn)B作BN⊥CD于N,
∵AC平分∠DCE,BN⊥CD,BE⊥CE,
∴BN=BE,
∵∠BND=∠CED=90°,∠BDN=∠CDE,
∴△BND∽△CED,
∴![]() ,
,
∴![]() ,
,
∵AO∥CE,
∴![]() =
=![]()
∴CE=2BE,CD=2DB,
設(shè)BE=x,BD=y,則CE=2x,CD=2y,
∵CD2=DE2+CE2,
∴4y2=(x+y)2+4x2,
∴(x+y)(5x﹣3y)=0,
∴y=![]() x,
x,
∴點(diǎn)C(x+1,2x),點(diǎn)D(1﹣![]() x,0)
x,0)
∵點(diǎn)C,點(diǎn)D是拋物線(xiàn)W:y=ax2﹣2上的點(diǎn),
∴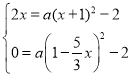
∴x+1=(1﹣![]() x)2,
x)2,
∴x1=0(舍去),x2=![]() ,
,
∴0=a(1﹣![]() )2﹣2,
)2﹣2,
∴a=![]() ,
,
∴拋物線(xiàn)解析式為:y=![]() x2﹣2;
x2﹣2;
(3)tan∠D1C1B恒為定值,
理由如下:由題意可得拋物線(xiàn)W1的解析式為:y=![]() x2﹣2﹣m,
x2﹣2﹣m,
設(shè)點(diǎn)D1的坐標(biāo)為(t,0)(t<0),
∴0=![]() t2﹣2﹣m,
t2﹣2﹣m,
∴2+m=![]() t2,
t2,
∴拋物線(xiàn)W1的解析式為:y=![]() x2﹣
x2﹣![]() t2,
t2,
∵拋物線(xiàn)W1與射線(xiàn)BC的交點(diǎn)為C1,
∴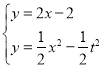
解得: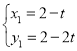 ,
,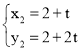 (不合題意舍去),
(不合題意舍去),
∴點(diǎn)C1的坐標(biāo)(2﹣t,2﹣2t),
如圖2,過(guò)點(diǎn)C1作C1H⊥x軸,過(guò)點(diǎn)C作CG⊥x軸,
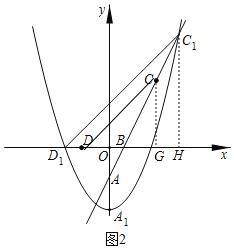
∴C1H=2﹣2t,OH=2﹣t,
∴D1H=D1O+OH=2﹣t+(﹣t)=2﹣2t,
∴C1H=D1H,且C1H⊥x軸,
∴∠C1D1H=45°,
∵y=![]() x2﹣2與x軸交于點(diǎn)D,
x2﹣2與x軸交于點(diǎn)D,
∴點(diǎn)D(﹣2,0)
∵y=2x﹣2與y=![]() x2﹣2交于點(diǎn)C,點(diǎn)A
x2﹣2交于點(diǎn)C,點(diǎn)A
∴點(diǎn)C(4,6)
∴GC=6,DG=OD+OG=2+4=6,
∴DG=CG,且CG⊥x軸,
∴∠GDC=45°=∠C1D1H,
∴C1D1∥CD,
∴∠D1C1B=∠DCB,
∴tan∠D1C1B=tan∠DCB,
如圖3,過(guò)點(diǎn)B作BF⊥CD于點(diǎn)F,
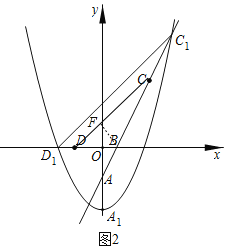
∵∠CDB=45°,BF⊥CD,BD=OD+OB=2+1=3,
∴∠FDB=∠FBD=45°,
∴DF=BF,DB=![]() DF=3,
DF=3,
∴DF=BF=![]()
∵點(diǎn)D(﹣2,0),點(diǎn)C(4,6),
∴CD=![]() =6
=6![]() ,
,
∴CF=CD﹣DF=![]() ,
,
∴tan∠D1C1B=tan∠DCB=![]() =
=![]() ,
,
∴tan∠D1C1B恒為定值.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
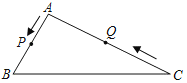
【題目】如圖,△ABC中,AB=8cm,AC=16cm,點(diǎn)P從A出發(fā),以每秒1厘米的速度向B運(yùn)動(dòng),點(diǎn)Q從C同時(shí)出發(fā),以每秒2厘米的速度向A運(yùn)動(dòng).其中一個(gè)動(dòng)點(diǎn)到達(dá)端點(diǎn)時(shí),另一個(gè)也相應(yīng)停止運(yùn)動(dòng).那么,當(dāng)以A、P、Q為頂點(diǎn)的三角形與△ABC相似時(shí),運(yùn)動(dòng)時(shí)間是_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】2019年中國(guó)北京世界園藝博覽會(huì)(以下簡(jiǎn)稱(chēng)“世園會(huì)”)于4月29日至10月7日在北京延慶區(qū)舉行.世園會(huì)為滿(mǎn)足大家的游覽需求,傾情打造了4條各具特色的趣玩路線(xiàn),分別是:![]() .“解密世園會(huì)”、
.“解密世園會(huì)”、![]() .“愛(ài)我家,愛(ài)園藝”、
.“愛(ài)我家,愛(ài)園藝”、![]() .“園藝小清新之旅”和
.“園藝小清新之旅”和![]() .“快速車(chē)覽之旅”.李欣和張帆都計(jì)劃暑假去世園會(huì),他們各自在這4條線(xiàn)路中任意選擇一條線(xiàn)路游覽,每條線(xiàn)路被選擇的可能性相同.
.“快速車(chē)覽之旅”.李欣和張帆都計(jì)劃暑假去世園會(huì),他們各自在這4條線(xiàn)路中任意選擇一條線(xiàn)路游覽,每條線(xiàn)路被選擇的可能性相同.
(1)李欣選擇線(xiàn)路![]() .“園藝小清新之旅”的概率是多少?
.“園藝小清新之旅”的概率是多少?
(2)用畫(huà)樹(shù)狀圖或列表的方法,求李欣和張帆恰好選擇同一線(xiàn)路游覽的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】下列說(shuō)法正確的是( )
A.擲一枚均勻的骰子,骰子停止轉(zhuǎn)動(dòng)后,6點(diǎn)朝上是必然事件
B.甲、乙兩人在相同條件下各射擊10次,他們的成績(jī)平均數(shù)相同,方差分別是S甲2=0.4,S乙2=0.6,則乙的射擊成績(jī)較穩(wěn)定
C.“明天降雨的概率為![]() ”,表示明天有半天都在降雨
”,表示明天有半天都在降雨
D.在3張卡片上分別寫(xiě)有實(shí)數(shù)0,![]() ,
,![]() ,從中隨機(jī)抽取一張,抽到無(wú)理數(shù)的概率是
,從中隨機(jī)抽取一張,抽到無(wú)理數(shù)的概率是![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
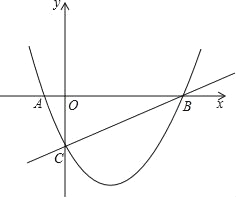
【題目】如圖,已知拋物線(xiàn)y=ax2﹣![]() x+c與x軸相交于A、B兩點(diǎn),并與直線(xiàn)y=
x+c與x軸相交于A、B兩點(diǎn),并與直線(xiàn)y=![]() x﹣2交于B、C兩點(diǎn),其中點(diǎn)C是直線(xiàn)y=
x﹣2交于B、C兩點(diǎn),其中點(diǎn)C是直線(xiàn)y=![]() x﹣2與y軸的交點(diǎn),連接AC.
x﹣2與y軸的交點(diǎn),連接AC.
(1)求拋物線(xiàn)的解析式;
(2)證明:△ABC為直角三角形;
(3)△ABC內(nèi)部能否截出面積最大的矩形DEFG?(頂點(diǎn)D、E、F、G在△ABC各邊上)若能,求出最大面積;若不能,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在正方形ABCD中,BE=EC,將正方形ABCD的邊CD沿DE折疊到DF,連接EF、FC、FB,若△DFC的面積為16,則△BEF的面積為_____.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
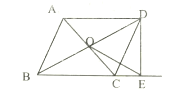
【題目】如圖,平行四邊形![]() 的對(duì)角線(xiàn)
的對(duì)角線(xiàn)![]() 、
、![]() 相交于點(diǎn)
相交于點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 是邊
是邊![]() 的延長(zhǎng)線(xiàn)上一點(diǎn),且
的延長(zhǎng)線(xiàn)上一點(diǎn),且![]() ,連接
,連接![]() .
.
(1)求證:![]() ;
;
(2)如果![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
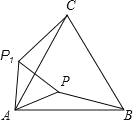
【題目】△ABC 是等邊三角形,點(diǎn) P 在△ABC 內(nèi),PA=2,將△PAB 繞點(diǎn) A 逆時(shí)針旋轉(zhuǎn)得到△P1AC,則 P1P 的長(zhǎng)等于( )
A. 2 B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com