
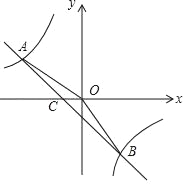
【題目】如圖,一次函數y=kx+b的圖象與反比例函數y=![]() 的圖象交于二象限內的A點和四象限內的B點,與x軸將于點C,連接AO,已知AO=2
的圖象交于二象限內的A點和四象限內的B點,與x軸將于點C,連接AO,已知AO=2![]() ,tan∠AOC=
,tan∠AOC=![]() ,點B的坐標為(a,﹣4).
,點B的坐標為(a,﹣4).
(1)求此反比例函數和一次函數的解析式;
(2)根據圖象寫出使一次函數的值小于反比例函數的值的x的取值范圍;
(3)求△AOB的面積.
【答案】(1)y=﹣![]() ,y=﹣x﹣2;(2)﹣4<x<0或x>2;(3)S△AOB=6.
,y=﹣x﹣2;(2)﹣4<x<0或x>2;(3)S△AOB=6.
【解析】
(1)先根據AO=2![]() ,tan∠AOC=
,tan∠AOC=![]() 求得點A的坐標,代入反比例函數解析式求得m的值,繼而得出點B的坐標,根據點A、B坐標可得一次函數解析式;
求得點A的坐標,代入反比例函數解析式求得m的值,繼而得出點B的坐標,根據點A、B坐標可得一次函數解析式;
(2)由函數圖象找到直線位于雙曲線下方所對應的x的范圍即可得;
(3)先求得點C坐標,再根據S△AOB=S△AOC+S△BOC求解可得.
(1)如圖,作AD⊥x軸于點D,
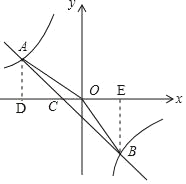
∵tan∠AOC=![]() =
=![]() ,
,
∴設AD=a、則OD=2a,
∴AO=![]() ,
,
則a=2,
∴AD=2、OD=4,
則點A坐標為(﹣4,2),
將點A坐標代入y=![]() ,得:m=﹣8,
,得:m=﹣8,
∴反比例函數解析式為y=﹣![]() ,
,
將點B(a,﹣4)代入y=﹣![]() ,得:a=2,
,得:a=2,
∴B(2,﹣4),
將點A、B坐標代入y=kx+b,
得:![]() ,
,
解得:![]() ,
,
則一次函數解析式為y=﹣x﹣2;
(2)由函數圖象知當﹣4<x<0或x>2時,一次函數的值小于反比例函數的值;
(3)在y=﹣x﹣2中當y=0時,﹣x﹣2=0,
解得:x=﹣2,
∴OC=2,
S△AOB=S△AOC+S△BOC
=![]() OCAD+
OCAD+![]() OCBE
OCBE
=![]() ×2×2+
×2×2+![]() ×2×4
×2×4
=2+4
=6.


 小夫子全能檢測系列答案
小夫子全能檢測系列答案科目:初中數學 來源: 題型:
【題目】如圖,旗桿AB的頂端B在夕陽的余輝下落在一個斜坡上的點D處,某校數學課外興趣小組的同學正在測量旗桿的高度,在旗桿的底部A處測得點D的仰角為15°,AC=10米,又測得∠BDA=45°.已知斜坡CD的坡度為i=1:![]() ,求旗桿AB的高度(
,求旗桿AB的高度(![]() ≈1.7,結果精確到個位).
≈1.7,結果精確到個位).

查看答案和解析>>
科目:初中數學 來源: 題型:
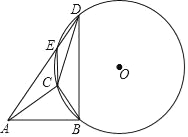
【題目】如圖,在Rt△ABC中,∠ACB=90°,AB=5,過點B作BD⊥AB,點C,D都在AB上方,AD交△BCD的外接圓⊙O于點E.
(1)求證:∠CAB=∠AEC.
(2)若BC=3.
①EC∥BD,求AE的長.
②若△BDC為直角三角形,求所有滿足條件的BD的長.
(3)若BC=EC=![]()
![]() ,則
,則![]() = .(直接寫出結果即可)
= .(直接寫出結果即可)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線![]() 與
與![]() 軸,
軸,![]() 軸分別交于點
軸分別交于點![]() ,經過點
,經過點![]() 的拋物線
的拋物線![]() 與
與![]() 軸的另一個交點為點
軸的另一個交點為點![]() ,點
,點![]() 是拋物線上一點,過點
是拋物線上一點,過點![]() 作
作![]() 軸于點
軸于點![]() ,連接
,連接![]() ,設點
,設點![]() 的橫坐標為
的橫坐標為![]() .
.
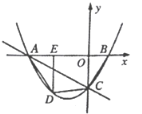
![]() 求拋物線的解析式;
求拋物線的解析式;
![]() 當點
當點![]() 在第三象限,設
在第三象限,設![]() 的面積為
的面積為![]() ,求
,求![]() 與
與![]() 的函數關系式,并求出
的函數關系式,并求出![]() 的最大值及此時點
的最大值及此時點![]() 的坐標;
的坐標;
![]() 連接
連接![]() ,若
,若![]() ,請直接寫出此時點
,請直接寫出此時點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線![]() 與
與![]() 軸,
軸,![]() 軸分別交于點
軸分別交于點![]() ,經過點
,經過點![]() 的拋物線
的拋物線![]() 與
與![]() 軸的另一個交點為點
軸的另一個交點為點![]() ,點
,點![]() 是拋物線上一點,過點
是拋物線上一點,過點![]() 作
作![]() 軸于點
軸于點![]() ,連接
,連接![]() ,設點
,設點![]() 的橫坐標為
的橫坐標為![]() .
.
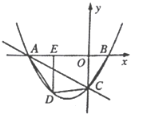
![]() 求拋物線的解析式;
求拋物線的解析式;
![]() 當點
當點![]() 在第三象限,設
在第三象限,設![]() 的面積為
的面積為![]() ,求
,求![]() 與
與![]() 的函數關系式,并求出
的函數關系式,并求出![]() 的最大值及此時點
的最大值及此時點![]() 的坐標;
的坐標;
![]() 連接
連接![]() ,若
,若![]() ,請直接寫出此時點
,請直接寫出此時點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我省中小學積極開展綜合實踐活動,某校準備組織開展四項綜合實踐活動:“A.我是非遺小傳人,B.學做家常餐,C.愛心義賣行動,D.找個崗位去體驗”.為了解學生最喜愛哪項綜合實踐活動,隨機抽取部分學生進行問卷調查(每位學生只能選擇一項),將調查結果繪制成下面兩幅不完整的統計圖,請結合圖中提供的信息回答下列問題:
(1)本次一共調查了 名學生,在扇形統計圖中,m的值是 ;
(2)補全條形統計圖;
(3)若該校共有1200名學生,估計最喜愛B和C項目的學生一共有多少名?
(4)現有最喜愛A,B,C,D活動項目的學生各一人,學校要從這四人中隨機選取兩人交流活動體會,請用列表或畫樹狀圖的方法求出恰好選取最喜愛C和D項目的兩位學生的概率.
最喜愛各項綜合實踐活動條形統計圖 最喜愛各項綜合實踐活動扇形統計圖


查看答案和解析>>
科目:初中數學 來源: 題型:
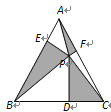
【題目】如圖,等邊△ABC中,P為三角形內一點,過P作PD⊥BC,PE⊥AB,PF⊥AC,連結AP、BP、CP,如果S△APF+S△BPE+S△PCD=![]() ,那么△ABC的內切圓半徑為___
,那么△ABC的內切圓半徑為___
查看答案和解析>>
科目:初中數學 來源: 題型:
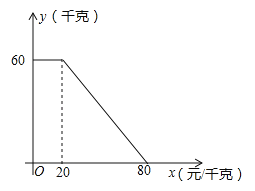
【題目】某商店以20元/千克的單價新進一批商品,經調查發現,在一段時間內,銷售量y(千克)與銷售單價x(元/千克)之間為一次函數關系,如圖所示.
(1)求y與x的函數表達式;
(2)要使銷售利潤達到800元,銷售單價應定為每千克多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com