
【題目】在![]() 中,
中,![]() 為直徑,弦
為直徑,弦![]() 交
交![]() 于點
于點![]() 、
、![]() ,連接
,連接![]() 、
、![]() ,
,![]() .
.
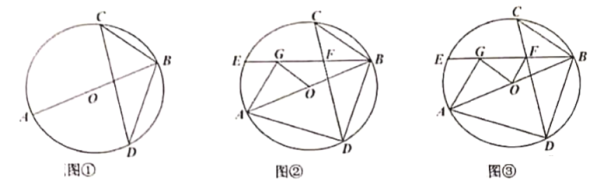
(1)如圖①,求![]() 的度數;
的度數;
(2)如圖②,弦![]() 交
交![]() 于點
于點![]() .在
.在![]() 上取點
上取點![]() ,連接
,連接![]() 、
、![]() 和
和![]() ,使
,使![]() ,求證:
,求證:![]() ;
;
(3)如圖③,在(2)的條件下,![]() ,
,![]() 的直徑為
的直徑為![]() ,連接
,連接![]() ,
,![]() ,求
,求![]() 的長.
的長.
 名師點撥卷系列答案
名師點撥卷系列答案 英才計劃期末調研系列答案
英才計劃期末調研系列答案科目:初中數學 來源: 題型:
【題目】數學學習小組“陸月輝煌”最近正在進行幾何圖形組合問題的研究.認真研讀以下四個片段,并回答問題.
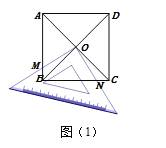
(片斷一)小陸說:將一塊足夠大的等腰直角三角板置于一個正方形中,直角頂點與對角線交點O重合,在轉動三角板的過程中我發現某些線段之間存在確定的數量關系.
如圖(1),若三角板兩條直角邊的外沿分別交正方形的邊AB、BC于點M、N,則①OM+ON=MB+NB;②![]() .
.
請你判斷他的猜想是否正確?并證明你認為正確的猜想.
(片斷二)小月說:將三角板中一個45°角的頂點和正方形的一個頂點重合放置,使得這個角的兩條邊與正方形的一組鄰邊有交點.
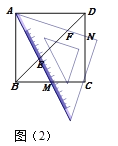
如圖(2),若以A為頂點的45°角的兩邊分別交正方形的邊BC、CD于點M、N,交對角線BD于點E、F.我發現:BE2+DE2=2AE2,只要準確旋轉圖(2)中的一個三角形就能證明這個結論.
請你寫出小月所說的具體的旋轉方式:______________________.
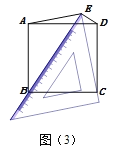
(片斷三)小輝說:將三角板的一個45°角放置在正方形的外部,同時角的兩邊恰好經過正方形兩個相鄰的頂點.
如圖(3),設頂點為E的45°角位于正方形的邊AD上方,這個角的兩邊分別經過點B、C,連接EA,ED.那么線段EB、EC、ED也存在確定的數量關系:(EB+ED)2=2EC2.
請你證明這個結論.
(片斷四)小煌說:在圖(2)中,作一個過點A、E、F的圓,交正方形的邊AB、AD于點G、H,如圖(4)所示.你知道線段DH、HG、GB三者之間的關系嗎?請直接寫出結論:________________.
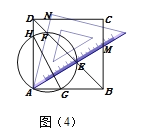
查看答案和解析>>
科目:初中數學 來源: 題型:
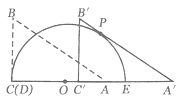
【題目】如圖,將直角三角板![]() 的直角邊
的直角邊![]() 放在半圓
放在半圓![]() 的直徑
的直徑![]() 上,直角頂點
上,直角頂點![]() 與直徑端點
與直徑端點![]() 重合,已知
重合,已知![]() ,且
,且![]() 的直角邊
的直角邊![]() 與半圓
與半圓![]() 的半徑
的半徑![]() 長均為2.現將直角三角板
長均為2.現將直角三角板![]() 沿直徑
沿直徑![]() 的方向向右平移,將三角板
的方向向右平移,將三角板![]() 平移后的三角形記為
平移后的三角形記為![]() .
.
(1)如圖,當![]() 平移到斜邊與半圓相切時,試求
平移到斜邊與半圓相切時,試求![]() 的長度(結果保留
的長度(結果保留![]() );
);
(2)設平移距離為![]() ,在直角三角形
,在直角三角形![]() 平移過程中,折線
平移過程中,折線![]() (包括端點)與半圓弧共有3個交點時,求
(包括端點)與半圓弧共有3個交點時,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
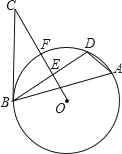
【題目】如圖,△ABD是⊙O的內接三角形,E是弦BD的中點,點C是⊙O外一點且∠DBC=∠A,連接OE延長與圓相交于點F,與BC相交于點C.
(1)求證:BC是⊙O的切線;
(2)若⊙O的半徑為6,BC=8,求弦BD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,![]() 中,
中,![]() 是
是![]() 邊上一點,
邊上一點,![]() 是
是![]() 的中點,過點
的中點,過點![]() 作
作![]() 的平行線交
的平行線交![]() 的延長線于
的延長線于![]() ,且
,且![]() ,連接
,連接![]() .
.
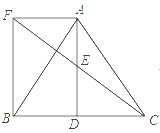
(1)求證:![]() 是
是![]() 的中點;
的中點;
(2)若![]() ,試判斷四邊形
,試判斷四邊形![]() 的形狀,并證明你的結論.
的形狀,并證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數y=ax2+bx+c的圖象所示,下列結論中:①abc>0;②2a+b=0;③當m≠1時,a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,則x1+x2=2,其中正確的結論分別是___.
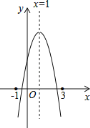
查看答案和解析>>
科目:初中數學 來源: 題型:
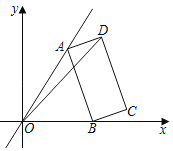
【題目】如圖,在平面直角坐標系中,點A在一次函數y=![]() x位于第一象限的圖象上運動,點B在x軸正半軸上運動,在AB右側以它為邊作矩形ABCD,且AB=2
x位于第一象限的圖象上運動,點B在x軸正半軸上運動,在AB右側以它為邊作矩形ABCD,且AB=2![]() ,AD=1,則OD的最大值是( )
,AD=1,則OD的最大值是( )
A.![]() B.
B.![]() +2C.
+2C.![]() +2D.
+2D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com