
【題目】如圖,直線![]() 與x軸交于點B,與y軸交于點C,拋物線
與x軸交于點B,與y軸交于點C,拋物線![]() 經過B、C兩點,且與x軸交于另一點A.
經過B、C兩點,且與x軸交于另一點A.
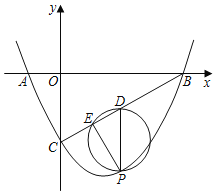
(1)求拋物線的解析式.
(2)點P是線段BC下方的拋物線上的動點(不與點B、C重合),過P作PD∥y軸交BC于點D,以PD為直徑的圓交BC于另一點E,求DE的最大值及此時點P的坐標;
(3)當(2)中的DE取最大值時,將△PDE繞點D旋轉,當點P落在坐標軸上時,求點E的坐標.
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣2;(2)m=2時,DE有最大值
x﹣2;(2)m=2時,DE有最大值![]() ,此時P
,此時P![]() ;(3)
;(3)![]() ,或E
,或E![]() 或
或![]()
【解析】
(1)求出![]() ,
,![]() ,將
,將![]() 與
與![]() 代入拋物線解析式即可求出
代入拋物線解析式即可求出![]() 、
、![]() 的值,進而確定函數解析式;
的值,進而確定函數解析式;
(2)設![]() ,可得
,可得![]() ,利用P、D的坐標表示出PD,再由點到直線距離公式求得線段PE的代數式,根據勾股定理求得線段DE的代數式,通過整理即可得到當
,利用P、D的坐標表示出PD,再由點到直線距離公式求得線段PE的代數式,根據勾股定理求得線段DE的代數式,通過整理即可得到當![]() 時,
時,![]() 有最大值
有最大值![]() ,此時
,此時![]() ;
;
(3)當點P落在坐標軸上時,先求出P點坐標,再分三種情況討論:①當![]() 時;②當
時;②當![]() ;③
;③![]() ;分別求出
;分別求出![]() 點坐標即可.
點坐標即可.
解:(1)在直線![]() 中,
中,
當![]() 時,
時,![]() ,即
,即![]() ,
,
當![]() 時,
時,![]() ,即
,即![]()
將![]() ,
,![]() 分別代入
分別代入![]() 得:
得:
![]() ,
,
解得: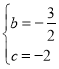 ,
,
![]() ;
;
(2)設![]() ,
,
![]() 是線段
是線段![]() 下方,
下方,
![]() ,
,
直線![]() 的解析式為
的解析式為![]() ,
,
![]() 軸與
軸與![]() 交于點
交于點![]() ,
,
![]() ,
,
![]() ,
,
![]() ,則PE為點P到直線BC:
,則PE為點P到直線BC:![]() 的距離,
的距離,
∴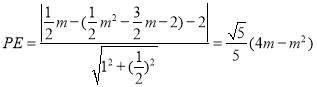 ,
,
在![]() 中,由勾股定理得:
中,由勾股定理得:![]() ,
,
∴![]() ,
,
當![]() 時,
時,![]() 有最大值
有最大值![]() ,此時
,此時![]() ;
;
(3)由(2)可知,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
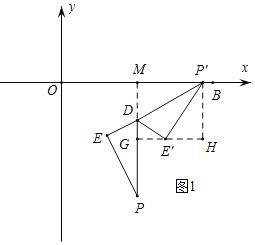
①如圖1,當P點落在如圖所示的位置,即![]() ,延長
,延長![]() 與
與![]() 軸交于點
軸交于點![]() ,
,
![]() ,
,![]() ,
,
∵![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ,
,
過點![]() 作
作![]() ,過點
,過點![]() 作
作![]() 交
交![]() 的延長線于點
的延長線于點![]() ;
;
![]() ,
,
∴∠DE'G+∠E'DG=∠DE'G+∠P' E'H=90°,
∴∠E'DG=∠P' E'H,
∴△DGE'∽△E'HP',
![]()
![]() ,
,
![]()
![]() ,
,
設![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]()
![]()
整理得: ,解得:
,解得: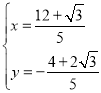 ,
,
∴![]() ;
;
②如圖2,![]() 與
與![]() 關于
關于![]() 對稱,
對稱,
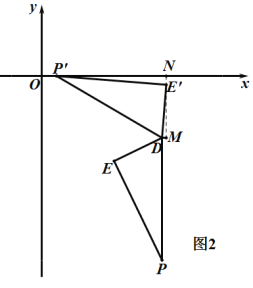
∴![]() ,
,
過點![]() 作
作![]() 軸垂線
軸垂線![]() ,過點D作DM⊥
,過點D作DM⊥![]() 交
交![]() 的延長線于點M,
的延長線于點M,
同理①得:△DME'∽△E'NP',
∴![]() ,
,
![]()
![]() ,
,
設![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
整理得: ,解得:
,解得: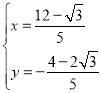 ,
,
∴![]() ;
;
③如圖3,![]() 在y軸上,
在y軸上,
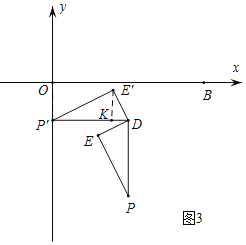
∵![]() ,
,
![]() ,
,
![]() ,
,
過點![]() 作
作![]() ,
,
設![]() ,則
,則![]() ,
,![]() ,
,
在![]() △
△![]() 中,
中,![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ;
;
綜上所述:當點P落在坐標軸上時,點E的坐標為![]() 或
或![]() 或
或![]() .
.


 小學學習好幫手系列答案
小學學習好幫手系列答案 小學同步三練核心密卷系列答案
小學同步三練核心密卷系列答案科目:初中數學 來源: 題型:
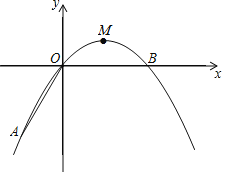
【題目】如圖,已知在平面直角坐標系xOy中,頂點為M的拋物線C1:y=ax2+bx(a<0)經過點A和x軸上的點B,AO=OB=2,∠AOB=120°.
(1)求該拋物線的表達式;
(2)連結AM,求S△AOM;
(3)設點F是x軸上一點,如果△MBF與△AOM相似,求所有符合條件的點F的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
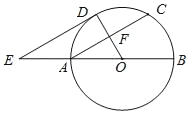
【題目】如圖,AB為⊙O的直徑,F為弦AC的中點,連接OF并延長交弧AC于點D,過點D作⊙O的切線,交BA的延長線于點E.
(1)求證:AC∥DE;
(2)連接AD、CD、OC.填空
①當∠OAC的度數為 時,四邊形AOCD為菱形;
②當OA=AE=2時,四邊形ACDE的面積為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校積極推行“互動生成的學本課堂”卓有成效,“小組合作學習”深入人心,九年級某學習小組在操作實踐過程中發現了一個有趣的問題:將直尺和三角板(三角板足夠大)按如圖所示的方式擺放在平面直角坐標系中,直尺的左側邊CD在直線x=4上,在保證直角三角板其中一條直角邊始終過點A(0,4),同時使得直角頂點E在CD上滑動,三角板的另一直角邊與x軸交于點B,當點E從點C(4,5)滑動到點D(4,0)的過程中,點B所經過的路徑長為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
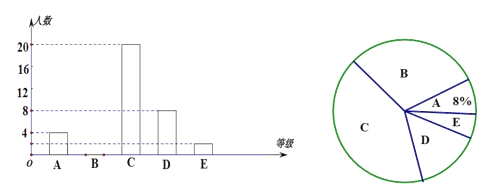
【題目】2020的寒假是一個特殊的假期.由于“新型冠狀肺炎病毒”影響,學校的開學日期不斷延后,在這期間某中學在學校微信公眾號上積極鼓勵學生靜在家中沉下心來參加“靜讀名著”活動,活動以讀名著的本書多少設為A,B,C,D,E五個等級,(本數依次為5,4,3,2,1),該校八(3)班全體學生參加了這次靜在家中沉下心來讀名著活動,芳芳同學通過調查并將這次讀書閱讀本數的結果繪制成如下兩幅不完整的統計圖.請根據圖中信息,解答下列問題:
(1)該校八(3)班共有______學生;
(2)扇形統計圖中B等級所對應扇形的圓心角等于______度;
(3)補全條形統計圖;
(4)若該校有學生2500人讀名著的本書在B、C級的人數一共有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形 ABCD 中,AD∥BC,AB=BC,對角線 AC、BD 交于點 O,BD 平分∠ABC,過點 D 作 DE⊥BC 交 BC 的延長線于點 E.連接 OE.
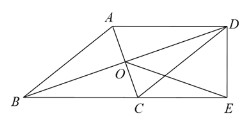
(1)求證:四邊形 ABCD 是菱形;
(2)若 tan∠DBC=![]() ,AB=
,AB=![]() ,求線段 OE 的長.
,求線段 OE 的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
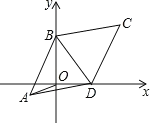
【題目】如圖,已知平行四邊形ABCD中,AB=BC,BC=10,∠BCD=60°,兩頂點B、D分別在平面直角坐標系的y軸、x軸的正半軸上滑動,連接OA,則OA的長的最小值是_____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com