
【題目】某客商準備采購一批特色商品,經調查,用16000元采購A型商品的件數是用7500元采購B型商品的件數的2倍,一件A型商品的進價比一件B型商品的進價多10元.
(1)求一件A,B型商品的進價分別為多少元?
(2)若該客商購進A,B型商品共250件進行試銷,其中A型品的件數不大于B型商品的件數,且不小于80件,已知A型商品的售價為240元/件,B型商品的售價為220元/件,且全部售出,設購進A型商品m件,求該客商銷售這批商品的利潤y與m之間的函數關系式,并寫出m的取值范圍;
(3)在(2)的條件下,客商決定在試銷活動中每售出一件A型商品,就從一件A型商品的利潤中捐獻慈善資金a元(0<a<80),若該客商售完所有商品并捐獻資金后獲得的最大收益是17100元,求的a值.
【答案】(1)一件B型商品的進價為150元,則一件A型商品的進價為160元;(2)![]() ,80≤m≤125;(3)a值為15
,80≤m≤125;(3)a值為15
【解析】
(1)設一件B型商品的進價為x元,則一件A型商品的進價為![]() 元.根據16000元采購A型商品的件數是用7500元采購B型商品的件數的2倍,列出方程即可解決問題;
元.根據16000元采購A型商品的件數是用7500元采購B型商品的件數的2倍,列出方程即可解決問題;
(2)根據總利潤=兩種商品的利潤之和,列出式子即可解決問題;
(3)設利潤為![]() 元.則
元.則![]() ,分三種情形討論即可解決問題,把
,分三種情形討論即可解決問題,把![]() 代入解答即可.
代入解答即可.
解:(1)設一件B型商品的進價為x元,則一件A型商品的進價為![]() 元,
元,
由題意:![]() ,
,
解得![]() ,
,
經檢驗![]() 是分式方程的解,
是分式方程的解,
答:一件B型商品的進價為150元,則一件A型商品的進價為160元;
(2)因為客商購進A型商品m件,所以客商購進B型商品![]() 件,
件,
由題意:![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ;
;
(3)設利潤為![]() 元.則
元.則![]() ,
,
①當![]() 時,即
時,即![]() 時,w隨m的增大而增大,所以
時,w隨m的增大而增大,所以![]() 時,最大利潤為
時,最大利潤為![]() 元;
元;
②當![]() 時,最大利潤為17500元;
時,最大利潤為17500元;
③當![]() 時,即
時,即![]() 時,w隨m的增大而減小,所以
時,w隨m的增大而減小,所以![]() 時,最大利潤為
時,最大利潤為![]() 元,
元,
∴![]() 或
或![]() ,
,
解得![]() (不合題意,舍去)或15.
(不合題意,舍去)或15.
答:若該客商售完所有商品并捐獻資金后獲得的最大收益是17100元,則a值為15.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】已知函數![]() ,小李同學對該函數的圖象與性質進行了探究,下面是小李同學探究的過程,補充完整:
,小李同學對該函數的圖象與性質進行了探究,下面是小李同學探究的過程,補充完整:
(1)直接寫出自變量x的取值范圍:__________;
(2)下表是y與x的幾組對應值:
x | … | -4 | -1 | 0 |
| 1 |
|
| 3 |
| 4 | 5 | n | … |
y | … |
| m |
| 0 | -1 | -4 | 8 | 5 | 4 |
| 3 |
| … |
則m= ,n= ;
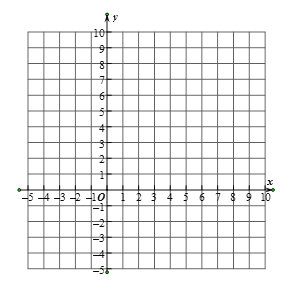
(3)如圖所示,在平面直角坐標系xoy中,描出以上表中各對對應值為坐標的點,并根據描出的點,畫出該函數的圖象;
(4)觀察函數圖象可知:該函數圖象的對稱中心的坐標是______;
(5)當![]() 時,關于x的方程
時,關于x的方程![]() 有實數解,直接寫出k的取值范圍_______.
有實數解,直接寫出k的取值范圍_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
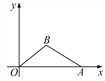
【題目】如圖,在直角坐標系內,O為原點,點A的坐標為(10,0),點B在第一象限內,BO=5,sin∠BOA=![]() . 求:(1)點B的坐標;(2)cos∠BAO的值.
. 求:(1)點B的坐標;(2)cos∠BAO的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
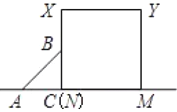
【題目】已知,如圖等腰直角![]() 沿MN所在的直線以
沿MN所在的直線以![]() 的速度向右作勻速直線運動,若
的速度向右作勻速直線運動,若![]() ,則
,則![]() 和正方形
和正方形![]() 重疊部分的面積
重疊部分的面積![]() 與勻速運動所有的時間
與勻速運動所有的時間![]() 之間函數的大致圖像是( )
之間函數的大致圖像是( )
A.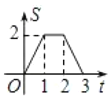 B.
B.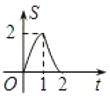 C.
C.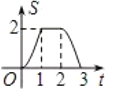 D.
D.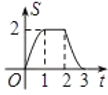
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB為⊙O的直徑,直線CD切⊙O于點M,BE⊥CD于點E.
(1)求證:∠BME=∠MAB;
(2)求證:BM2=BEAB;
(3)若BE=![]() ,sin∠BAM=
,sin∠BAM=![]() ,求線段AM的長.
,求線段AM的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“2018杭州馬拉松競賽”的個人競賽項目共有三項:A.“馬拉松”,B.“半程馬拉松”,C.“迷你馬拉松”.小明和小剛參加了該賽事的志愿者服務工作,組委會隨機將志愿者分配到三個項目組.
(1)小明被分配到“迷你馬拉松”項目組的概率為![]() ______.
______.
(2)請用畫樹狀圖或列表的方法,求出小明和小剛被分配到同一項目組的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】修建隧道可以方便出行.如圖:![]() ,
,![]() 兩地被大山阻隔,由
兩地被大山阻隔,由![]() 地到
地到![]() 地需要爬坡到山頂
地需要爬坡到山頂![]() 地,再下坡到
地,再下坡到![]() 地.若打通穿山隧道,建成直達
地.若打通穿山隧道,建成直達![]() ,
,![]() 兩地的公路,可以縮短從
兩地的公路,可以縮短從![]() 地到
地到![]() 地的路程.已知:從
地的路程.已知:從![]() 到
到![]() 坡面的坡度
坡面的坡度![]() ,從
,從![]() 到
到![]() 坡面的坡角
坡面的坡角![]() ,
,![]() 公里.
公里.
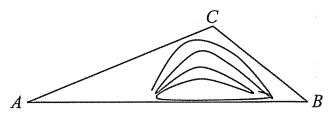
(1)求隧道打通后從![]() 到
到![]() 的總路程是多少公里?(結果保留根號)
的總路程是多少公里?(結果保留根號)
(2)求隧道打通后與打通前相比,從![]() 地到
地到![]() 地的路程約縮短多少公里?(結果精確到0.01)(
地的路程約縮短多少公里?(結果精確到0.01)(![]() ,
,![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題探究
(1)如圖1.在![]() 中,
中,![]() ,
,![]() 為
為![]() 上一點,
上一點,![]() .則
.則![]() 面積的最大值是_______.
面積的最大值是_______.
(2)如圖2,在![]() 中,
中,![]() ,
,![]() 為
為![]() 邊上的高,
邊上的高,![]() 為
為![]() 的外接圓,若
的外接圓,若![]() ,試判斷
,試判斷![]() 是否存在最小值?若存在,請求出最小值:若不存在,請說明理由.
是否存在最小值?若存在,請求出最小值:若不存在,請說明理由.
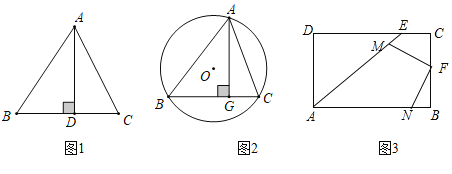
問題解決:
如圖3,王老先生有一塊矩形地![]() ,
,![]() ,
,![]() ,現在他想利用這塊地建一個四邊形魚塘
,現在他想利用這塊地建一個四邊形魚塘![]() ,且滿足點
,且滿足點![]() 在
在![]() 上,
上,![]() ,點
,點![]() 在
在![]() 上,且
上,且![]() ,點
,點![]() 在
在![]() 上,點
上,點![]() 在
在![]() 上,
上,![]() ,這個四邊形
,這個四邊形![]() 的面積是否存在最大值?若存在,求出面積的最大值;若不存在,請說明理由.
的面積是否存在最大值?若存在,求出面積的最大值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com