
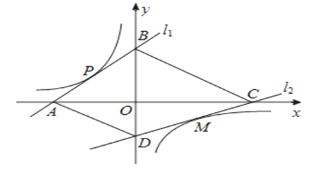
【題目】如圖,直線l1解析式為y=x+2,且與坐標(biāo)軸分別交于A、B兩點(diǎn),與雙曲線交于點(diǎn)P(﹣1,1).點(diǎn)M是雙曲線在第四象限上的一點(diǎn),過點(diǎn)M的直線l2與雙曲線只有一個(gè)公共點(diǎn),并與坐標(biāo)軸分別交于點(diǎn)C、點(diǎn)D,當(dāng)四邊形ABCD的面積取最小值時(shí),則點(diǎn)M的坐標(biāo)為( )
A. (1,﹣1) B. (2,﹣![]() ) C. (3,﹣
) C. (3,﹣![]() ) D. 不能確定
) D. 不能確定
【答案】A
【解析】
先求出A、B兩點(diǎn)的坐標(biāo),有P(﹣1,1)在反比例函數(shù)圖象上求得解析式為y![]() ,設(shè)M點(diǎn)橫坐標(biāo)為a,進(jìn)而可得M點(diǎn)坐標(biāo)(a,
,設(shè)M點(diǎn)橫坐標(biāo)為a,進(jìn)而可得M點(diǎn)坐標(biāo)(a,![]() );再設(shè)直線l2的解析式為y=bx+c,根據(jù)條件“過點(diǎn)M的直線l2與雙曲線只有一個(gè)公共點(diǎn)”,將M點(diǎn)坐標(biāo)代入直線l2的解析式,求得用a表示的C、D兩點(diǎn)坐標(biāo).由A、B、C、D四點(diǎn)坐標(biāo),可得AC、BD的長(zhǎng),因?yàn)?/span>AC⊥BD,有S四邊形ABCD
);再設(shè)直線l2的解析式為y=bx+c,根據(jù)條件“過點(diǎn)M的直線l2與雙曲線只有一個(gè)公共點(diǎn)”,將M點(diǎn)坐標(biāo)代入直線l2的解析式,求得用a表示的C、D兩點(diǎn)坐標(biāo).由A、B、C、D四點(diǎn)坐標(biāo),可得AC、BD的長(zhǎng),因?yàn)?/span>AC⊥BD,有S四邊形ABCD![]() ACBD,據(jù)此得到一個(gè)關(guān)于a的式子,通過化簡(jiǎn)、配方即可求得S四邊形ABCD的最小值,故可得出a的值,由此得出結(jié)論.
ACBD,據(jù)此得到一個(gè)關(guān)于a的式子,通過化簡(jiǎn)、配方即可求得S四邊形ABCD的最小值,故可得出a的值,由此得出結(jié)論.
∵直線l1解析式為y=x+2,且與坐標(biāo)軸分別交于A、B兩點(diǎn),∴A(﹣2,0),B(0,2).
設(shè)反比例函數(shù)的解析式為y![]() .
.
∵點(diǎn)P(﹣1,1)在反比例函數(shù)y![]() 的圖象上,∴k=xy=﹣1,∴反比例函數(shù)的解析式為y
的圖象上,∴k=xy=﹣1,∴反比例函數(shù)的解析式為y![]() .
.
∵點(diǎn)M在第四象限,且在反比例函數(shù)y![]() 的圖象上,∴可設(shè)點(diǎn)M的坐標(biāo)為(a,
的圖象上,∴可設(shè)點(diǎn)M的坐標(biāo)為(a,![]() ),其中a>0.
),其中a>0.
設(shè)直線l2的解析式為y=bx+c,則ab+c![]() ,∴c
,∴c![]() ab,∴y=bx
ab,∴y=bx![]() ab.
ab.
∵直線y=bx![]() ab與雙曲線y
ab與雙曲線y![]() 只有一個(gè)交點(diǎn),∴方程bx
只有一個(gè)交點(diǎn),∴方程bx![]() ab
ab![]() 即bx2﹣(
即bx2﹣(![]() ab)x+1=0有兩個(gè)相等的實(shí)根,∴[﹣(
ab)x+1=0有兩個(gè)相等的實(shí)根,∴[﹣(![]() ab)]2﹣4b=(
ab)]2﹣4b=(![]() ab)2﹣4b=(
ab)2﹣4b=(![]() ab)2=0,∴
ab)2=0,∴![]() ab,∴b
ab,∴b![]() ,c
,c![]() ,∴直線l2的解析式為y
,∴直線l2的解析式為y![]() ,∴當(dāng)x=0時(shí),y
,∴當(dāng)x=0時(shí),y![]() ,則點(diǎn)D的坐標(biāo)為(0,
,則點(diǎn)D的坐標(biāo)為(0,![]() );
);
當(dāng)y=0時(shí),x=2a,則點(diǎn)C的坐標(biāo)為(2a,0),∴AC=2a﹣(﹣2)=2a+2,BD=2﹣(![]() )=2
)=2![]() .
.
∵AC⊥BD,∴S四邊形ABCD![]() ACBD
ACBD![]() (2a+2)(2
(2a+2)(2![]() )=4+2(a
)=4+2(a![]() )=4+2[(
)=4+2[(![]() )2+2]
)2+2]
=8+2(![]() )2.
)2.
∵(![]() )2≥0,∴S四邊形ABCD≥8,∴當(dāng)且僅當(dāng)(
)2≥0,∴S四邊形ABCD≥8,∴當(dāng)且僅當(dāng)(![]() )2=0,即a=1時(shí),四邊形有最小值,∴M(1,﹣1).
)2=0,即a=1時(shí),四邊形有最小值,∴M(1,﹣1).
故選A.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,在![]() 中,
中,![]() ,
,![]() ,將
,將![]() 繞點(diǎn)
繞點(diǎn)![]() 旋轉(zhuǎn),邊
旋轉(zhuǎn),邊![]() 分別交邊
分別交邊![]() 、
、![]() 于
于![]() 、
、![]() 兩點(diǎn).
兩點(diǎn).
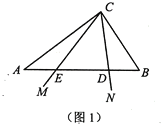

(1)若![]() ,
,![]() ,求
,求![]() 的最小值;
的最小值;
(2)如圖2,設(shè)![]() ,點(diǎn)
,點(diǎn)![]() 是
是![]() 的中點(diǎn),連接
的中點(diǎn),連接![]() ,當(dāng)
,當(dāng)![]() 旋轉(zhuǎn)到
旋轉(zhuǎn)到![]() 與
與![]() 的交點(diǎn)
的交點(diǎn)![]() 是
是![]() 的中點(diǎn)時(shí),過點(diǎn)
的中點(diǎn)時(shí),過點(diǎn)![]() 作
作![]() 的垂線交CM于點(diǎn)
的垂線交CM于點(diǎn)![]() ,連接
,連接![]() 、
、![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,將矩形ABCO放在直角坐標(biāo)系中,其中頂點(diǎn)B的坐標(biāo)為(10, 8),E是BC邊上一點(diǎn)將△ABE沿AE折疊,點(diǎn)B剛好與OC邊上點(diǎn)D重合,過點(diǎn)E的反比例函數(shù)y=![]() 的圖象與邊AB交于點(diǎn)F, 則線段AF的長(zhǎng)為( )
的圖象與邊AB交于點(diǎn)F, 則線段AF的長(zhǎng)為( )

A. ![]() B. 2 C.
B. 2 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】“十九大”報(bào)告提出了我國將加大治理環(huán)境污染的力度,還我青山綠水,其中霧霾天氣讓環(huán)保和健康問題成為焦點(diǎn),為了調(diào)查學(xué)生對(duì)霧霾天氣知識(shí)的了解程度,某校在全校學(xué)生中抽取400名同學(xué)做了一次調(diào)查,根據(jù)調(diào)查統(tǒng)計(jì)結(jié)果,繪制了不完整的一種統(tǒng)計(jì)圖表.
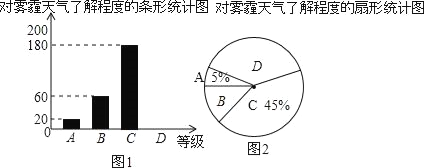
對(duì)霧霾了解程度的統(tǒng)計(jì)表
對(duì)霧霾的了解程度 | 百分比 |
A.非常了解 | 5% |
B.比較了解 | m |
C.基本了解 | 45% |
D.不了解 | n |
請(qǐng)結(jié)合統(tǒng)計(jì)圖表,回答下列問題:
(1)統(tǒng)計(jì)表中:m= ,n= ;
(2)請(qǐng)?jiān)趫D1中補(bǔ)全條形統(tǒng)計(jì)圖;
(3)請(qǐng)問在圖2所示的扇形統(tǒng)計(jì)圖中,D部分扇形所對(duì)應(yīng)的圓心角是多少度?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,一垂直于地面的燈柱AB被一鋼筋CD固定,CD與地面成45°夾角(∠CDB=45°),在C點(diǎn)上方2米處加固另一條鋼線ED,ED與地面成53°夾角(∠EDB=53°),那么鋼線ED的長(zhǎng)度約為多少米?(結(jié)果精確到1米,參考數(shù)據(jù):sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】去學(xué)校食堂就餐,經(jīng)常會(huì)在一個(gè)買菜窗口前等待,經(jīng)調(diào)查發(fā)現(xiàn),同學(xué)的舒適度指數(shù)y與等時(shí)間x(分)之間滿足反比例函數(shù)關(guān)系,如下表:
等待時(shí)間x | 1 | 2 | 5 | 10 | 20 |
舒適度指數(shù)y | 100 | 50 | 20 | 10 | 5 |
已知學(xué)生等待時(shí)間不超過30分鐘
(1)求y與x的函數(shù)關(guān)系式,并寫出自變量x的取值范圍.
(2)若等待時(shí)間8分鐘時(shí),求舒適度的值;
(3)舒適度指數(shù)不低于10時(shí),同學(xué)才會(huì)感到舒適.請(qǐng)說明,作為食堂的管理員,讓每個(gè)在窗口買菜的同學(xué)最多等待多少時(shí)間?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,四邊形ABCD是⊙O的內(nèi)接四邊形,AC為直徑,點(diǎn)B是弧AC的中點(diǎn),若AC=7,BD=6,則由四個(gè)弓形組成的陰影部分的面積為_____.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知:如圖,AB是⊙O的直徑,點(diǎn)P在BA的延長(zhǎng)線上,弦CD交AB于E,連接OD、PC、BC,∠AOD=2∠ABC,∠P=∠D,過E作弦GF⊥BC交圓與G、F兩點(diǎn),連接CF、BG.則下列結(jié)論:①CD⊥AB;②PC是⊙O的切線;③OD∥GF;④弦CF的弦心距等于![]() BG.則其中正確的是( )
BG.則其中正確的是( )
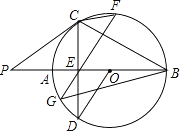
A. ①②④ B. ③④ C. ①②③ D. ①②③④
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
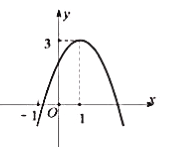
【題目】二次函數(shù)![]() 的圖像如圖所示,下列結(jié)論正確是( )
的圖像如圖所示,下列結(jié)論正確是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]() 有兩個(gè)不相等的實(shí)數(shù)根
有兩個(gè)不相等的實(shí)數(shù)根
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com