【題目】某校興趣小組在創客嘉年華活動中組織了計算機編程比賽，八年級每班派25名學生參加，成績分別為
、
、
、
四個等級．其中相應等級的得分依次記為10分、9分、8分、7分．將八年級的一班和二班的成績整理并繪制成如下統計圖表：
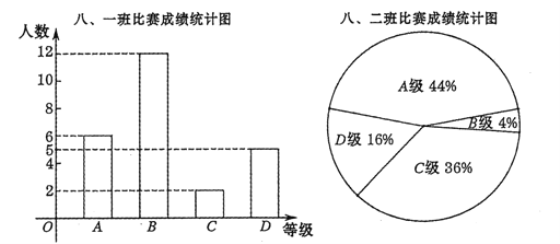
班級 | 平均數（分） | 中位數（分） | 眾數（分） | 方差 |
一班 | 8．76 | 9 | 9 |
|
二班 | 8．76 | 8 | 10 |
|
請根據本學期所學過的《數據的分析》相關知識分析上述數據，幫助計算機編程老師選擇一個班級參加校級比賽，并闡述你選擇的理由．
口算題天天練系列答案科目：初中數學 來源： 題型：
【題目】設a，b，c是△ABC的三條邊，關于x的方程
x2+
x+c-a=0有兩個相等的實數根，方程3cx+2b=2a的根為x=0.
（1）試判斷△ABC的形狀；
（2）若a，b為方程x2+mx-3m=0的兩個根，求m的值.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖,BD是△ABC的角平分線,點E,F分別在BC,AB上,且DE∥AB,BE=AF.
(1)求證:四邊形ADEF是平行四邊形;
(2)若∠ABC=60°,BD=6,求DE的長.
查看答案和解析>>
科目：初中數學 來源： 題型：
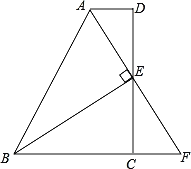
【題目】如圖，在四邊形ABCD中，AD∥BC，E為CD的中點，連接AE、BE，BE⊥AE，延長AE交BC的延長線于點F．
求證：(1)FC＝AD；(2)AB＝BC+AD．
查看答案和解析>>
科目：初中數學 來源： 題型：
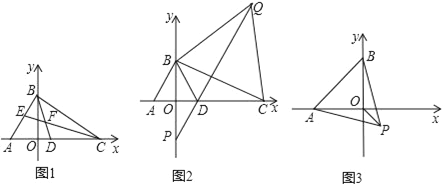
【題目】如圖，在平面直角坐標系中，A（﹣3，0），點 B是 y軸正半軸上一動點，點C、D在 x正半軸上．
（1）如圖，若∠BAO＝60°，∠BCO＝40°，BD、CE 是△ABC的兩條角平分線，且BD、CE交于點F，直接寫出CF的長_____．
（2）如圖，△ABD是等邊三角形，以線段BC為邊在第一象限內作等邊△BCQ，連接 QD并延長，交 y軸于點 P，當點 C運動到什么位置時，滿足 PD＝
DC？請求出點C的坐標；
（3）如圖，以AB為邊在AB的下方作等邊△ABP，點B在 y軸上運動時，求OP的最小值．
查看答案和解析>>
科目：初中數學 來源： 題型：
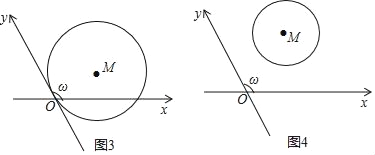
【題目】我們知道，平面內互相垂直且有公共原點的兩條數軸構成平面直角坐標系，如果兩條數軸不垂直，而是相交成任意的角ω（0°＜ω＜180°且ω≠90°），那么這兩條數軸構成的是平面斜坐標系，兩條數軸稱為斜坐標系的坐標軸，公共原點稱為斜坐標系的原點，如圖1，經過平面內一點P作坐標軸的平行線PM和PN，分別交x軸和y軸于點M，N．點M、N在x軸和y軸上所對應的數分別叫做P點的x坐標和y坐標，有序實數對（x，y）稱為點P的斜坐標，記為P（x，y）．
（1）如圖2，ω＝45°，矩形OABC中的一邊OA在x軸上，BC與y軸交于點D，OA＝2，OC＝l．
①點A、B、C在此斜坐標系內的坐標分別為A ，B ，C ．
②設點P（x，y）在經過O、B兩點的直線上，則y與x之間滿足的關系為 ．
③設點Q（x，y）在經過A、D兩點的直線上，則y與x之間滿足的關系為 ．
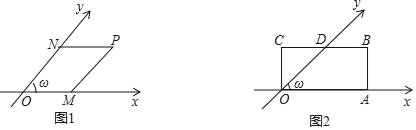
（2）若ω＝120°，O為坐標原點．
①如圖3，圓M與y軸相切原點O，被x軸截得的弦長OA＝4
，求圓M的半徑及圓心M的斜坐標．
②如圖4，圓M的圓心斜坐標為M（2，2），若圓上恰有兩個點到y軸的距離為1，則圓M的半徑r的取值范圍是 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，A(-3，3)，B(-4，-2)，C(-1，-1)．
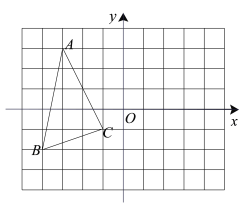
（1）在圖中作出△ABC關于y軸對稱的△A＇B＇C＇，并寫出點C＇的坐標________；
（2）在y軸上畫出點P，使PA+PC最小，并直接寫出P點坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，
，
，且
，
滿足
，直線
經過點
和
．
（1） 點的坐標為（ ， ）， 點的坐標為（ ， ）；
（2）如圖1，已知直線
經過點 和
軸上一點
，
，點
在直線AB上且位于軸右側圖象上一點，連接
，且
．
①求點坐標；
②將
沿直線AM 平移得到
，平移后的點
與點重合，
為
上的一動點，當
的值最小時，請求出最小值及此時 N 點的坐標；
（3）如圖 2，將點向左平移 2 個單位到點
，直線
經過點和
，點
是點關于軸的對稱點，直線
經過點
和點
,動點
從原點出發沿著
軸正方向運動，連接
，過點作直線的垂線交軸于點
，在直線
上是否存在點
，使得
是等腰直角三角形？若存在，求出點坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，平面直角坐標系中，
、
，且
、
滿足
(1)求
、
兩點的坐標；
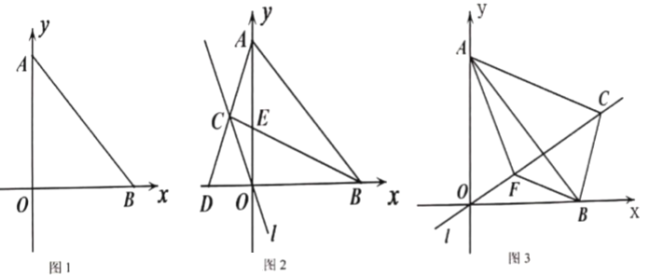
(2)過點
的直線
上有一點
，連接
、
，
，如圖2，當點在第二象限時，交
軸于點
，延長交
軸于點
，設
的長為
，
的長為
，用含的式子表示；
(3)在(2)的條件下，如圖3，當點在第一象限時，過點作
交
于點
，連接
，若
，
，求的長．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
