
【題目】如圖,平面直角坐標系中,![]() 、
、![]() ,且
,且![]() 、
、![]() 滿足
滿足![]()
(1)求![]() 、
、![]() 兩點的坐標;
兩點的坐標;
(2)過點![]() 的直線
的直線![]() 上有一點
上有一點![]() ,連接
,連接![]() 、
、![]() ,
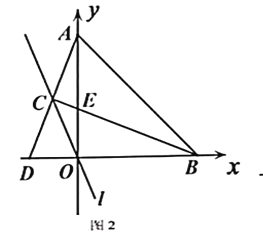
,![]() ,如圖2,當點
,如圖2,當點![]() 在第二象限時,
在第二象限時,![]() 交
交![]() 軸于點
軸于點![]() ,延長
,延長![]() 交
交![]() 軸于點
軸于點![]() ,設
,設![]() 的長為
的長為![]() ,
,![]() 的長為
的長為![]() ,用含
,用含![]() 的式子表示
的式子表示![]() ;
;
(3)在(2)的條件下,如圖3,當點![]() 在第一象限時,過點
在第一象限時,過點![]() 作
作![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的長.
的長.
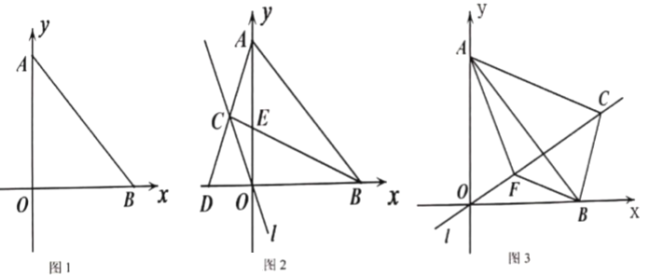
【答案】(1)A(0,5)、B(5,0);(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)先根據非負數的性質求出a、b的值,進而可得結果;
(2)先根據余角的性質證得∠DAO=∠CBD,進而可根據ASA證明△ADO≌△BEO,可得![]() ,進一步即可得出d和m的關系式;
,進一步即可得出d和m的關系式;
(3)過點![]() 作
作![]() 于
于![]() ,
,![]() 交CB延長線于點
交CB延長線于點![]() ,根據四邊形的內角和和平角的定義易得
,根據四邊形的內角和和平角的定義易得![]() ,從而可根據AAS證明△OAM≌△OBN,可得
,從而可根據AAS證明△OAM≌△OBN,可得![]() ,可得CO是直角∠ACB的平分線,進一步即可推出
,可得CO是直角∠ACB的平分線,進一步即可推出![]() ,過點
,過點![]() 作
作![]() 于
于![]() ,由等腰直角三角形的性質可得
,由等腰直角三角形的性質可得![]() ,進而可得
,進而可得![]() ,然后即可根據SAS證明△AOF≌△OBK,可得
,然后即可根據SAS證明△AOF≌△OBK,可得![]() ,然后再利用等腰直角三角形的性質和角平分線的性質得出BC和AC的關系,進而可得結果.
,然后再利用等腰直角三角形的性質和角平分線的性質得出BC和AC的關系,進而可得結果.
解:(1)∵![]() ,
,![]() ,
,
![]() ,∴A(0,5)、B(5,0);
,∴A(0,5)、B(5,0);
(2)如圖2,![]() ,
,![]() ,
,
![]() ,
,![]() ,∴∠DAO=∠CBD,
,∴∠DAO=∠CBD,
∵AO=BO=5,∠DOA=∠EOB=90°,
∴△ADO≌△BEO(ASA),![]()
![]() ,
,![]() ;
;
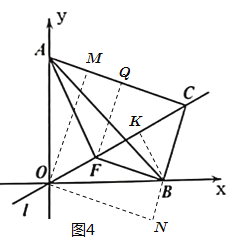
(3)過點![]() 作
作![]() 于
于![]() ,
,![]() 交CB延長線于點
交CB延長線于點![]() ,如圖4,
,如圖4,![]() ,
,
∵四邊形![]() 的內角和為
的內角和為![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,∴△OAM≌△OBN(AAS),
,∴△OAM≌△OBN(AAS),
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
過點![]() 作
作![]() 于
于![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,∴△AOF≌△OBK(SAS),
,∴△AOF≌△OBK(SAS),
![]() ,
,![]() ,
,
過點![]() 作
作![]() 于
于![]() ,
,![]() ,
,
![]() ,
,![]() .
.


 口算心算速算應用題系列答案
口算心算速算應用題系列答案 同步拓展閱讀系列答案
同步拓展閱讀系列答案科目:初中數學 來源: 題型:
【題目】下列說法正確的是
A. “明天降雨的概率是80%”表示明天有80%的時間都在降雨
B. “拋一枚硬幣正面朝上的概率為![]() ”表示每拋2次就有一次正面朝上
”表示每拋2次就有一次正面朝上
C. “彩票中獎的概率為1%”表示買100張彩票肯定會中獎
D. “拋一枚正方體骰子,朝上的點數為2的概率為![]() ”表示隨著拋擲次數的增加,“拋出朝上的點數為2”這一事件發生的頻率穩定在
”表示隨著拋擲次數的增加,“拋出朝上的點數為2”這一事件發生的頻率穩定在![]() 附近
附近
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩名隊員參加射擊訓練,成績分別被制成下列兩個統計圖:

根據以上信息,整理分析數據如下:
平均成績/環 | 中位數/環 | 眾數/環 | 方差 | |
甲 | a | 7 | 7 | 1.2 |
乙 | 7 | b | 8 | c |
(1)寫出表格中a,b,c的值;
(2)分別運用表中的四個統計量,簡要分析這兩名隊員的射擊訓練成績.若選派其中一名參賽,你認為應選哪名隊員.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知AB是⊙O的直徑,BP是⊙O的弦,弦CD⊥AB于點F,交BP于點G,E在CD的延長線上,EP=EG,

(1)求證:直線EP為⊙O的切線;
(2)點P在劣弧AC上運動,其他條件不變,若BG2=BFBO.試證明BG=PG;
(3)在滿足(2)的條件下,已知⊙O的半徑為3,sinB=![]() .求弦CD的長.
.求弦CD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某市郊外景區內一條筆直的公路a經過三個景點A、B、C,景區管委會又開發了風景優美的景點D,經測量景點D位于景點A的北偏東30°方向8km處,位于景點B的正北方向,還位于景點C的北偏西75°方向上,已知AB=5km.

(1)景區管委會準備由景點D向公路a修建一條距離最短的公路,不考慮其它因素,求出這條公路的長;(結果精確到0.1km)
(2)求景點C與景點D之間的距離.(結果精確到1km)
(參考數據:![]() =1.73,
=1.73,![]() =2.24,sin53°=cos37°=0.80,sin37°=cos53°=0.60,tan53°=1.33,tan37°=0.75,sin38°=cos52°=0.62,sin52°=cos38°=0.79,tan38°=0.78,tan52°=1.28,sin75°=0.97,cos75°=0.26,tan75°=3.73.)
=2.24,sin53°=cos37°=0.80,sin37°=cos53°=0.60,tan53°=1.33,tan37°=0.75,sin38°=cos52°=0.62,sin52°=cos38°=0.79,tan38°=0.78,tan52°=1.28,sin75°=0.97,cos75°=0.26,tan75°=3.73.)
查看答案和解析>>
科目:初中數學 來源: 題型:
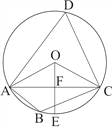
【題目】如圖,四邊形ABCD 是⊙O的內接四邊形,∠ABC=2∠D,連接OA,OC,AC
(1)求∠OCA的度數 (2)如果OE![]() AC于F,且OC=
AC于F,且OC=![]() , 求AC的長
, 求AC的長
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】列方程解應用題:
某玩具廠生產一種玩具,按照控制固定成本降價促銷的原則,使生產的玩具能夠及時售出,據市場調查:每個玩具按![]() 元銷售時,每天可銷售
元銷售時,每天可銷售![]() 個;若銷售單價每降低元,每天可多售出
個;若銷售單價每降低元,每天可多售出![]() 個.已知每個玩具的固定成本為
個.已知每個玩具的固定成本為![]() 元,問這種玩具的銷售單價為多少元時,廠家每天可獲利潤
元,問這種玩具的銷售單價為多少元時,廠家每天可獲利潤![]() 元?
元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校初二數學興趣小組活動時,碰到這樣一道題:
“已知正方形![]() ,點
,點![]() 分別在邊
分別在邊![]() 上,若
上,若![]() ,則
,則![]() ”.
”.
經過思考,大家給出了以下兩個方案:
(甲)過點![]() 作
作![]() 交
交![]() 于點
于點![]() ,過點
,過點![]() 作
作![]() 交
交![]() 于點
于點![]() ;
;
(乙)過點![]() 作
作![]() 交
交![]() 于點
于點![]() ,作
,作![]() 交
交![]() 的延長線于點
的延長線于點![]() ;同學們順利地解決了該題后,大家琢磨著想改變問題的條件,作更多的探索.
;同學們順利地解決了該題后,大家琢磨著想改變問題的條件,作更多的探索.
(1)對小杰遇到的問題,請在甲、乙兩個方案中任選一個,加以證明(如圖1);


圖1 圖2
(2)如果把條件中的“![]() ”改為“
”改為“![]() 與
與![]() 的夾角為
的夾角為![]() ”,并假設正方形
”,并假設正方形![]() 的邊長為l,
的邊長為l,![]() 的長為
的長為![]() (如圖2),試求
(如圖2),試求![]() 的長度.
的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在等腰Rt△ABC中,斜邊AB=8,點P在以AC為直徑的半圓上,M為PB的中點,當點P沿半圓從點A運動至點C時,點M運動的路徑長是( )

A. 2![]() π B.
π B. ![]() π C. 2π D. 2
π C. 2π D. 2![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com