【題目】某大型企業為了保護環境，準備購買A、B兩種型號的污水處理設備共8臺，用于同時治理不同成分的污水，若購買A型2臺、B型3臺需54萬，購買A型4臺、B型2臺需68萬元．
（1）求出A型、B型污水處理設備的單價；
（2）經核實，一臺A型設備一個月可處理污水220噸，一臺B型設備一個月可處理污水190噸，如果該企業每月的污水處理量不低于1565噸，請你為該企業設計一種最省錢的購買方案．
【答案】（1）A型污水處理設備的單價為12萬元，B型污水處理設備的單價為10萬元；（2）購進2臺A型污水處理設備，購進6臺B型污水處理設備最省錢．
【解析】試題分析：（1）根據題意結合購買A型2臺、B型3臺需54萬，購買A型4臺、B型2臺需68萬元分別得出等式求出答案；
（2）利用該企業每月的污水處理量不低于1565噸，得出不等式求出答案．
試題解析：（1）設A型污水處理設備的單價為x萬元，B型污水處理設備的單價為y萬元，根據題意可得： 
，解得： 
．
答：A型污水處理設備的單價為12萬元，B型污水處理設備的單價為10萬元；
（2）設購進a臺A型污水處理器，根據題意可得：
220a+190（8﹣a）≥1565，解得：a≥1.5，∵A型污水處理設備單價比B型污水處理設備單價高，∴A型污水處理設備買越少，越省錢，∴購進2臺A型污水處理設備，購進6臺B型污水處理設備最省錢．
閱讀快車系列答案科目：初中數學 來源： 題型：
【題目】如圖是我市某一天內的氣溫變化圖，根據圖象，下列說法中錯誤的是( )
A.這一天中最高氣溫是26℃
B.這一天中最高氣溫與最低氣溫的差為16℃
C.這一天中2時至14時之間的氣溫在逐漸升高
D.這一天中14時至24時之間的氣溫在逐漸降低
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】課上教師呈現一個問題
甲、乙、丙三位同學用不同的方法添加輔助線解決問題，如下圖：
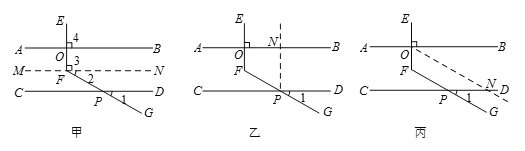
甲同學輔助線的做法和分析思路如下：
（1）請你根據乙同學所畫的圖形，描述輔助線的做法，并寫出相應的分析思路.
輔助線：___________________；
分析思路：
（2）請你根據丙同學所畫的圖形，求∠EFG的度數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，電線桿CD上的C處引拉線CE，CF固定電線桿，在離電線桿6米的B處安置測角儀（點B，E，D在同一直線上），在A處測得電線桿上C處的仰角為30°，已知測角儀的高AB=1.5米，BE=2.3米，求拉線CE的長，（精確到0.1米）參考數據
≈1.41，
≈1.73．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系中，拋物線y=ax2﹣5ax+4a與x軸交于A、B（A點在B點的左側）與y軸交于點C．
（1）如圖1，連接AC、BC，若△ABC的面積為3時，求拋物線的解析式；
（2）如圖2，點P為第四象限拋物線上一點，連接PC，若∠BCP=2∠ABC時，求點P的橫坐標；
（3）如圖3，在（2）的條件下，點F在AP上，過點P作PH⊥x軸于H點，點K在PH的延長線上，AK=KF，∠KAH=∠FKH，PF=﹣4
a，連接KB并延長交拋物線于點Q，求PQ的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】“龜兔首次賽跑”之后，輸了比賽的兔子沒有氣餒，總結反思后，和烏龜約定再賽一場．圖中的圖象刻畫了“龜兔再次賽跑”的故事（
表示烏龜從起點出發所行的時間，
表示烏龜所行的路程，
表示兔子所行的路程）．
①“龜兔再次賽跑”的路程為______米；
②兔子比烏龜晚出發______分鐘；
③烏龜在途中休息了______分鐘；
④烏龜的速度是______米/分；
⑤兔子的速度是______米/分；
⑥兔子在距起點______米處追上烏龜．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】學完二次根式一章后，小易同學看到這樣一題：“函數
中,自變量
的取值范圍是什么？”這個問題很簡單，根據二次根式的性質很容易得到自變量的取值范圍.聯想到一次函數，小易想進一步研究這個函數的圖象和性質.以下是他的研究步驟：
第一步：函數中,自變量的取值范圍是_____________.
第二步：根據自變量取值范圍列表：
| -1 | 0 | 1 | 2 | 3 | 4 | |
| 0 | 1 |
|
| 2 |
|
__________.
第三步：描點畫出函數圖象.
在描點的時候，遇到了
，
這樣的點，小易同學用所學勾股定理的知識，找到了畫圖方法，如圖所示：
你能否從中得到啟發，在下面的
軸上標出表示
、
、
的點，并畫出的函數圖象.
第四步：分析函數的性質.
請寫出你發現的函數的性質(至少寫兩條)：
____________________________________________________________________________________________
____________________________________________________________________________________________
第五步：利用函數圖象解含二次根式的方程和不等式.
（1）請在上面坐標系中畫出
的圖象，并估算方程
的解.
（2）不等式
的解是__________________.
查看答案和解析>>
科目：初中數學 來源： 題型：
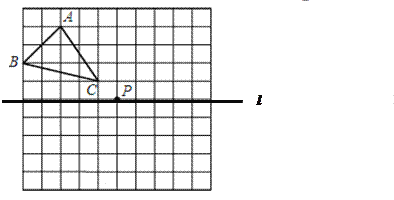
【題目】如圖，一個10×10網格，每個小正方形的邊長均為1，每個小正方形的頂點叫格點，△ABC的頂點均在格點上．
（1）畫出△ABC關于直線l的對稱的△A1B1C1．
（2）畫出△ABC關于點P的中心對稱圖形△A2B2C2．
（3）△A1B1C1與△A2B2C2組成的圖形_______________（是或否）軸對稱圖形，如果是軸對稱圖形，請畫出對稱軸．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
