
【題目】如圖,把矩形紙片ABCD沿EF翻折,點A恰好落在BC邊的A′處,若AB= ![]() ,∠EFA=60°,則四邊形A′B′EF的周長是( )
,∠EFA=60°,則四邊形A′B′EF的周長是( )

A. 1+3![]() B. 3+
B. 3+![]() C. 4+
C. 4+![]() D. 5+
D. 5+![]()
【答案】D
【解析】試題分析:如圖,
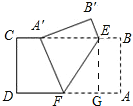
過點E作EG⊥AD,
∴∠AGE=∠FGE=90°
∵矩形紙片ABCD,
∴∠A=∠B=∠AGE=90°,
∴四邊形ABEG是矩形,
∴BE=AG,EG=AB=![]() ,
,
在Rt△EFG中,∠EFG=60°,EG=![]() ,
,
∴FG=1,EF=2,
由折疊有,A'F=AF,A'B'=AB=![]() ,BE=B'E,∠A'FE=∠AFE=60°,
,BE=B'E,∠A'FE=∠AFE=60°,
∵BC∥AD,
∴∠A'EF=∠AFE=60°,
∴△A'EF是等邊三角形,
∴A'F=EF=2,
∴AF=A'F=2,
∴BE=AG=AF-FG=2-1=1
∴B'E=1
∴四邊形A′B′EF的周長是A'B'+B'E+EF+A'F=![]() +1+2+2=5+
+1+2+2=5+![]() ,
,
故答案為:5+![]() .
.


 輕巧奪冠周測月考直通高考系列答案
輕巧奪冠周測月考直通高考系列答案科目:初中數學 來源: 題型:
【題目】為了更好改善河流的水質,治污公司決定購買10臺污水處理設備![]() 現有A,B兩種型號的設備,其中每臺的價格,月處理污水量如下表:經調查:購買一臺A型設備比購買一臺B型設備多2萬元,購買2臺A型設備比購買3臺B型設備少6萬元.
現有A,B兩種型號的設備,其中每臺的價格,月處理污水量如下表:經調查:購買一臺A型設備比購買一臺B型設備多2萬元,購買2臺A型設備比購買3臺B型設備少6萬元.
A型 | B型 | |
價格 | a | b |
處理污水量 | 240 | 200 |
![]() 求a,b的值;
求a,b的值;
![]() 治污公司經預算購買污水處理設備的資金不超過105萬元,你認為該公司有哪幾種購買方案;
治污公司經預算購買污水處理設備的資金不超過105萬元,你認為該公司有哪幾種購買方案;
![]() 在
在![]() 的條件下,若每月要求處理污水量不低于2040噸,為了節約資金,請你為治污公司設計一種最省錢的購買方案.
的條件下,若每月要求處理污水量不低于2040噸,為了節約資金,請你為治污公司設計一種最省錢的購買方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為響應區“美麗廣西 清潔鄉村”的號召,某校開展“美麗廣西 清潔校園”的活動,該校經過精心設計,計算出需要綠化的面積為498m2 , 綠化150m2后,為了更快的完成該項綠化工作,將每天的工作量提高為原來的1.2倍.結果一共用20天完成了該項綠化工作.該項綠化工作原計劃每天完成多少m2?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面魚角坐標系xOy中,A(﹣3,0),點B為y軸正半軸上一點,將線段AB繞點B旋轉90°至BC處,過點C作CD垂直x軸于點D,若四邊形ABCD的面積為36,則線AC的解析式為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c的圖像如圖所示,對稱軸為直線x=1.有位學生寫出了以下五個結論:

(1)ac>0;
(2)方程ax2+bx+c=0的兩根是x1=-1,x2=3;
(3)2a-b=0;
(4)當x>1時,y隨x的增大而減小;
(5)3a+2b+c>0
則以上結論中不正確的有( )
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明想知道湖中兩個小亭A、B之間的距離,他在與小亭A、B位于同一水平面且東西走向的湖邊小道![]() 上某一觀測點M處,測得亭A在點M的北偏東30°方向, 亭B在點M的北偏東60°方向,當小明由點M沿小道
上某一觀測點M處,測得亭A在點M的北偏東30°方向, 亭B在點M的北偏東60°方向,當小明由點M沿小道![]() 向東走60米時,到達點N處,此時測得亭A恰好位于點N的正北方向,繼續向東走30米時到達點Q處,此時亭B恰好位于點Q的正北方向,根據以上測量數據,請你幫助小明計算湖中兩個小亭A、B之間的距離.
向東走60米時,到達點N處,此時測得亭A恰好位于點N的正北方向,繼續向東走30米時到達點Q處,此時亭B恰好位于點Q的正北方向,根據以上測量數據,請你幫助小明計算湖中兩個小亭A、B之間的距離.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是某貨站傳送貨物的平面示意圖. 為了提高傳送過程的安全性,工人師傅欲減小傳送帶與地面的夾角,使其由45°改為30°. 已知原傳送帶AB長為4米.
(1)求新傳送帶AC的長度;
(2)如果需要在貨物著地點C的左側留出2米的通道,試判斷距離B點4米的貨物![]() 是否需要挪走,并說明理由.
是否需要挪走,并說明理由.

【答案】(1)5.6m;(2)應挪走.
【解析】試題解析:試題分析:(1)在構建的直角三角形中,首先求出兩個直角三角形的公共直角邊,進而在Rt△ACD中,求出AC的長.
(2)通過解直角三角形,可求出BD、CD的長,進而可求出BC、PC的長.然后判斷PC的值是否大于2米即可.
試題解析:(1)如圖,
在Rt△ABD中,AD=ABsin45°=4![]() .
.
在Rt△ACD中,
∵∠ACD=30°,
∴AC=2AD=8.
即新傳送帶AC的長度約為8米;
(2)結論:貨物MNQP不用挪走.
解:在Rt△ABD中,BD=ABcos45°=4![]() =4.
=4.
在Rt△ACD中,CD=![]() AD=4
AD=4![]() .
.
∴CB=CD-BD=4![]() -4≈2.8.
-4≈2.8.
∵PC=PB-CB≈5-2.8=2.2>2,
∴貨物MNQP不應挪走.
【題型】解答題
【結束】
8
【題目】如圖有一圓錐形糧堆,其主視圖是邊長為6m的正三形ABC。
(1)求該圓錐形糧堆的側面積。
(2)母線AC的中點P處有一老鼠正在偷吃糧食,小貓從B處沿圓錐表面去偷襲老鼠,求小貓經過的最短路程。 (結果不取近似數)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對任意一個三位數n,如果n滿足各數位上的數字互不相同,且都不為零,那么稱這個數為“相異數” .將一個“相異數”任意兩個數位上的數字對調后可以得到三個不同的新三位數,把這三個新三位數的和與111的商記為F(n).例如n=123,對調百位與十位上的數字得到213,對調百位與個位上的數字得到321,對調十位與個位上的數字得到132,這三個新三位數的和為213+321+132=666,666÷111=6,所以F(123) =6.
(1)計算:F(315),F(746);
(2)若s、t都是“相異數”,其中s=100x+42,t=160+y(1≤x≤9,1≤y≤9,x、y都是正整數),當F(s)+F(t)=17時,求x、y的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
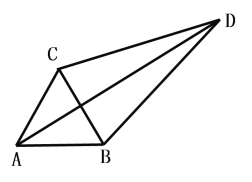
【題目】已知:△ABC為等邊三角形
(1)若D為△ABC外一點,滿足∠CDB=30,求證:![]()
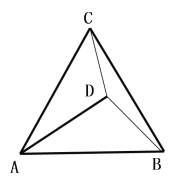
(2)若D為△ABC內一點,DC=3,DB=4,DA=5,求∠CDB的度數
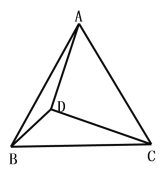
(3)若D為△ABC內一點,DA=4,DB=![]() ,DC=
,DC=![]() 則AB= (直接寫出答案)
則AB= (直接寫出答案)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com