
【題目】如圖,在平面直角坐標系中,點![]() ,
,![]() ,
,![]() ,線段
,線段![]() 經過平移得到線段
經過平移得到線段![]() ,其中點
,其中點![]() 的對應點為點
的對應點為點![]() ,點D在第一象限,直線AC交
,點D在第一象限,直線AC交![]() 軸于點
軸于點![]()
(1)點D坐標為
(2)線段![]() 由線段
由線段![]() 經過怎樣平移得到?
經過怎樣平移得到?
(3)求![]() 的面積.
的面積.

【答案】(1)![]() ;(2)向右平移5個單位,再向上平移3個單位;(3)
;(2)向右平移5個單位,再向上平移3個單位;(3)![]() .
.
【解析】
(1) 點![]() ,
,![]() ,
,![]() ,根據線段
,根據線段![]() 經過平移得到線段
經過平移得到線段![]() ,其中點
,其中點![]() 的對應點為點
的對應點為點![]() ,可得B點先向右平移5個單位,向上平移3個單位可得到點C,所以點A先向右平移5個單位,向上平移3個單位可得到點D
,可得B點先向右平移5個單位,向上平移3個單位可得到點C,所以點A先向右平移5個單位,向上平移3個單位可得到點D![]() , (2)點
, (2)點![]() 的對應點為點
的對應點為點![]() , 點A對應的點D,所以
, 點A對應的點D,所以![]() 先向右平移5個單位,向上平移3個單位平移得到線段
先向右平移5個單位,向上平移3個單位平移得到線段![]() , (3)
, (3)
(1) 因為點![]() ,
,![]() ,
,![]() ,且點
,且點![]() 的對應點為點
的對應點為點![]() ,
,
所以B點先向右平移5個單位,向上平移3個單位可得到點C,
所以點A先向右平移5個單位,向上平移3個單位可得到點D![]() ,
,
(2)因為點![]() 的對應點為點
的對應點為點![]() , 點A對應的點D,
, 點A對應的點D,
所以![]() 先向右平移5個單位,向上平移3個單位平移得到線段
先向右平移5個單位,向上平移3個單位平移得到線段![]() ,
,
(3)設直線AC的解析式為y=kx+b,
將點![]() ,
,![]() 代入可得:
代入可得:![]() ,解得:
,解得: ,
,
所以![]() ,
,
令![]() ,解得
,解得![]() ,
,
所以點F![]() ,
,
所以![]() 的面積=
的面積=![]() .
.


 口算心算速算應用題系列答案
口算心算速算應用題系列答案 同步拓展閱讀系列答案
同步拓展閱讀系列答案科目:初中數學 來源: 題型:
【題目】某牧區需要550頂帳篷過冬,現由甲、乙兩個工廠生產,已知甲工廠每天生產的能力是乙工廠的1.5倍,并且生產240頂帳篷甲工廠比乙工廠少4天,
(1)甲、乙兩個工廠每天分別生產多少頂帳篷?
(2)若甲工廠每天生產成本為3萬元,乙工廠每天生產成本為2.4萬元,要使這批帳篷的生產總成本不高于60萬元,至少應安排甲工廠生產多少天?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是二次函數![]() 圖象的一部分,圖象過點A(-3,0),對稱軸為直線
圖象的一部分,圖象過點A(-3,0),對稱軸為直線![]() ,下列結論:①
,下列結論:①![]() ;②
;②![]() ;③
;③![]() ;④若B(
;④若B(![]() ,
, ![]() )、C(
)、C(![]() ,
, ![]() )為函數圖象上的兩點,則
)為函數圖象上的兩點,則![]() .其中正確結論是( )
.其中正確結論是( )
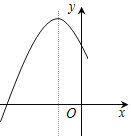
A. ②④ B. ①③ C. ①④ D. ②③
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E為AB的中點
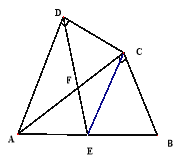
(1)求證:AC2=ABAD;
(2)求證:CE∥AD;
(3)若AD=4,AB=6,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知三角形ABC的三個頂點的坐標分別是A(0,3),B(0,1),C(2,1).若將三角形ABC向左平移3個單位長度,再向下平移1個單位長度得到三角形A′B′C′.
(1)寫出三角形A′B′C′各頂點的坐標;
(2)畫出三角形ABC和三角形A′B′C′;
(3)求出三角形A′B′C′的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平面直角坐標系中,正方形OBAC的頂點A的坐標為(8,8),點D,E分別為邊AB,AC上的動點,且不與端點重合,連接OD,OE,分別交對角線BC于點M,N,連接DE,若∠DOE=45°, 以下說法正確的是________(填序號).
①點O到線段DE的距離為8;②△ADE的周長為16;③當DE∥BC時,直線OE的解析式為y=![]() x; ④以三條線段BM,MN,NC為邊組成的三角形是直角三角形.
x; ④以三條線段BM,MN,NC為邊組成的三角形是直角三角形.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】規定:sin(-x)=-sinx,cos(-x)=cosx,sin(x+y)=sinx·cosy+cosx·siny.據此判斷下列等式成立的是_________(填序號).
①cos(-60°)=—cos60°=![]()
②sin75°=sin(30°+45°)=sin30°·cos45°+cos30°·sin45°=![]()
③sin2x=sin(x+x)=sinx·cosx+cosx·sinx=2sinx·cosx;
④sin(x-y)=sinx·cosy-cosx·siny.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們不妨約定:對角線互相垂直的凸四邊形叫做“十字形”.
(1)①在平行四邊形,矩形,菱形、正方形中,一定是十字形的有 ;
②若凸四邊形ABCD是十字形,AC=a,BD=b,則該四邊形的面積為 ;
(2)如圖1,以等腰Rt△ABC的底邊AC為邊作等邊三角形△ACD,連接BD,交AC于點O, 當 ![]() ≤S 四邊形≤
≤S 四邊形≤![]() 時,求BD的取值范圍;
時,求BD的取值范圍;
(3)如圖2,以十字形ABCD的對角線AC與BD為坐標軸,建立如圖所示的平面直角坐標系xOy,若計 十字形ABCD的面積為S,記△AOB,△COD,△AOD,△BOC的面積分別為:S1,S2,S3,S4,且同時滿足列四個條件:

①![]() ;②
;② ![]() ;③十字形ABCD的周長為32:④∠ABC=60°; 若E為OA的中點,F為線段BO上一動點,連接EF,動點P從點E出發,以1cm/s 的速度沿線段EF勻速運動到點F,再以2cms 的速度沿線段FB勻速運動到點B,到達點B 后停止運動,當點P沿上述路線運動 到點B所需要的時間最短時,求點P走完全程所需的時間及直線EF的解析式.
;③十字形ABCD的周長為32:④∠ABC=60°; 若E為OA的中點,F為線段BO上一動點,連接EF,動點P從點E出發,以1cm/s 的速度沿線段EF勻速運動到點F,再以2cms 的速度沿線段FB勻速運動到點B,到達點B 后停止運動,當點P沿上述路線運動 到點B所需要的時間最短時,求點P走完全程所需的時間及直線EF的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】【題目】如圖,在Rt△ABC中,∠C=90°,以AC為直徑作⊙O,交AB于D,過點O作OE∥AB,交BC于E.
(1)求證:ED為⊙O的切線;
(2)如果⊙O的半徑為![]() ,ED=2,延長EO交⊙O于F,連接DF、AF,求△ADF的面積.
,ED=2,延長EO交⊙O于F,連接DF、AF,求△ADF的面積.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com