
【題目】已知![]() 在數(shù)軸上的位置如圖所示,所對應(yīng)的點分別為
在數(shù)軸上的位置如圖所示,所對應(yīng)的點分別為![]() .
.
![]()
(1)在數(shù)軸上表示![]() 的點與表示
的點與表示![]() 的點之間的距離為 ;由此可得點
的點之間的距離為 ;由此可得點![]() 之間的距離為
之間的距離為
(2)化簡:![]()
(3)若![]() 的倒數(shù)是它本身,
的倒數(shù)是它本身,![]() 的絕對值的相反數(shù)是
的絕對值的相反數(shù)是![]() ,
,![]() 是數(shù)軸上表示
是數(shù)軸上表示![]() 的一點,且
的一點,且![]() ,求
,求![]() 所表示的數(shù).
所表示的數(shù).
【答案】(1)4;![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 所表示的數(shù)為
所表示的數(shù)為![]() 或
或![]() .
.
【解析】
(1)根據(jù)數(shù)軸的定義:兩點之間的距離即可得;
(2)根據(jù)數(shù)軸的定義,得出![]() 的符號、絕對值大小,再根據(jù)絕對值運算化簡即可;
的符號、絕對值大小,再根據(jù)絕對值運算化簡即可;
(3)先根據(jù)平方數(shù)、倒數(shù)、相反數(shù)的定義求出![]() 的值,再根據(jù)絕對值運算化簡求值即可得.
的值,再根據(jù)絕對值運算化簡求值即可得.
(1)由數(shù)軸的定義得:在數(shù)軸上表示![]() 的點與表示
的點與表示![]() 的點之間的距離為
的點之間的距離為![]() ;點
;點![]() 之間的距離為
之間的距離為![]()
故答案為:4;![]() ;
;
(2)由![]() 在數(shù)軸上的位置可知:
在數(shù)軸上的位置可知:![]()
則![]()
![]()
![]() ;
;
(3)由![]() 在數(shù)軸上的位置可知:
在數(shù)軸上的位置可知:![]()
由![]() 得,
得,![]() 或
或![]() (舍去)
(舍去)
由![]() 的倒數(shù)是它本身得,
的倒數(shù)是它本身得,![]() ,解得
,解得![]() 或
或![]() (舍去)
(舍去)
由![]() 的絕對值的相反數(shù)是
的絕對值的相反數(shù)是![]() 得,
得,![]() ,解得
,解得![]() 或
或![]() (舍去)
(舍去)
將![]() 代入得
代入得![]()
根據(jù)數(shù)軸的定義、絕對值運算分以下四部分討論:
①當(dāng)![]() 時,
時,![]()
解得![]() ,符合題設(shè)
,符合題設(shè)
②當(dāng)![]() 時,
時,![]()
解得![]() ,不符題設(shè),舍去
,不符題設(shè),舍去
③當(dāng)![]() 時,
時,![]()
解得![]() ,不符題設(shè),舍去
,不符題設(shè),舍去
④當(dāng)![]() 時,
時,![]()
解得![]() ,符合題設(shè)
,符合題設(shè)
綜上,![]() 所表示的數(shù)為
所表示的數(shù)為![]() 或
或![]() .
.


 新課標(biāo)階梯閱讀訓(xùn)練系列答案
新課標(biāo)階梯閱讀訓(xùn)練系列答案科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在矩形ABCD中,將△ABD沿AB向下平移使A點到達B點,得到△BEC,下列說法正確的是( )
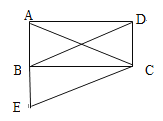
A. △ACE一定是等腰三角形B. △ACE一定是等邊三角形
C. △ACE一定是銳角三角形D. △ACE不可能是等腰直角三角形
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某書報亭開設(shè)兩種租書方式:一種是零星租書,每冊收費1元;另一種是會員卡租書,辦卡費每月12元,租書費每冊0.4元.小軍經(jīng)常來該店租書,若每月租書數(shù)量為x冊.
(1)寫出零星租書方式應(yīng)付金額![]() (元)與租書數(shù)量x(冊)之間的函數(shù)關(guān)系式。
(元)與租書數(shù)量x(冊)之間的函數(shù)關(guān)系式。
(2)寫出會員卡租書方式應(yīng)付金額![]() (元)與租書數(shù)量x(冊)之間的函數(shù)關(guān)系式.
(元)與租書數(shù)量x(冊)之間的函數(shù)關(guān)系式.
(3)小軍選取哪種租書方式更合算?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
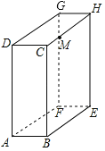
【題目】如圖,長方體的長BE=20cm,寬AB=10cm,高AD=15cm,點M在CH上,且CM=5cm,一只螞蟻如果要沿著長方體的表面從點A爬到點M,需要爬行的最短距離是多少?
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,CE⊥AB,BD⊥AC,垂足分別為E、D,BD、CE交于點O,AB=AC,∠B=20°,則∠AOD=( )

A. 20°B. 40°C. 50°D. 55°
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)軸上A,B兩點對應(yīng)的數(shù)分別為a,b,且a,b滿足|a+20|=﹣(b﹣13)2,點C對應(yīng)的數(shù)為16,點D對應(yīng)的數(shù)為﹣13.
(1)求a,b的值;
(2)點A,B沿數(shù)軸同時出發(fā)相向勻速運動,點A的速度為6個單位/秒,點B的速度為2個單位/秒,若t秒時點A到原點的距離和點B到原點的距離相等,求t的值;
(3)在(2)的條件下,點A,B從起始位置同時出發(fā).當(dāng)A點運動到點C時,迅速以原來的速度返回,到達出發(fā)點后,又折返向點C運動.B點運動至D點后停止運動,當(dāng)B停止運動時點A也停止運動.求在此過程中,A,B兩點同時到達的點在數(shù)軸上對應(yīng)的數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】閱讀下面的文字,解答問題
大家知道![]() 是無理數(shù),而無理數(shù)是無限不循環(huán)小數(shù),因此
是無理數(shù),而無理數(shù)是無限不循環(huán)小數(shù),因此![]() 的小數(shù)部分我們不可能全部地寫出來,于是小明用
的小數(shù)部分我們不可能全部地寫出來,于是小明用![]() ﹣1來表示
﹣1來表示![]() 的小數(shù)部分,你同意小明的表示方法嗎?
的小數(shù)部分,你同意小明的表示方法嗎?
事實上,小明的表示方法是有道理的,因為![]() 的整數(shù)部分是1,將這個數(shù)減去其整數(shù)部分,差就是小數(shù)部分.
的整數(shù)部分是1,將這個數(shù)減去其整數(shù)部分,差就是小數(shù)部分.
又例如:![]() <
<![]() <
<![]() ,即2<
,即2<![]() <3,
<3,
∴![]() 的整數(shù)部分為2,小數(shù)部分為(
的整數(shù)部分為2,小數(shù)部分為(![]() ﹣2)
﹣2)
請解答:
(1)![]() 整數(shù)部分是 ,小數(shù)部分是 .
整數(shù)部分是 ,小數(shù)部分是 .
(2)如果![]() 的小數(shù)部分為a,
的小數(shù)部分為a,![]() 的整數(shù)部分為b,求|a﹣b|+
的整數(shù)部分為b,求|a﹣b|+![]() 的值.
的值.
(3)已知:9+![]() =x+y,其中x是整數(shù),且0<y<1,求x﹣y的相反數(shù).
=x+y,其中x是整數(shù),且0<y<1,求x﹣y的相反數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
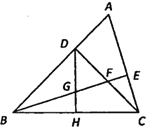
【題目】如圖,在△ABC中,∠ABC=45°,CD⊥AB于點D,BE平分∠ABC,且BE⊥AC于點E,與CD相交于點F,H是邊BC的中點,連接 DH與 BE相交于點 G,若GE=3,則BF=_____.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com