
【題目】如圖,在平面直角坐標系xOy中,以點P(﹣3,4)為圓心的⊙P與y軸相切,A是x軸上一動點,過A點的直線與⊙P相切于點B,以AB為邊作正方形ABCD,則正方形ABCD面積的最小值為_____.
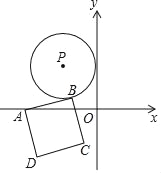
【答案】7.
【解析】
由切線的性質得到PB⊥AB,則在直角△APB中,AB2=AP2-PB2,PB=3為定值,欲求正方形ABCD面積即AB2的最小值,只需AP取最小值即可,當AP⊥x軸時,AP最小,則易得正方形ABCD面積的最小值.
解:∵以點P(-3,4)為圓心的⊙P與y軸相切,
∴⊙P的半徑為3.
如圖,連接AP、PB.
∵AB與⊙P相切且點B為切點,
∴PB⊥AB,則在直角△APB中,AB2=AP2-PB2,即AB2=AP2-9.
∵PB=3為定值,
∴當AP取最小值時,AB的值最小.當AP⊥x軸時,AP最小,此時AP=4,
∴AB2=42-9=7.
∴正方形ABCD面積的最小值=AB2=7.
故答案是:7.


科目:初中數學 來源: 題型:
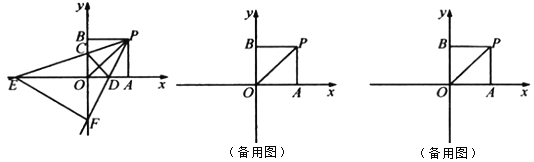
【題目】如圖,在平面直角坐標系中,正方形![]() 的邊長為
的邊長為![]() ,點
,點![]() ,
,![]() 分別在
分別在![]() 軸正半軸與
軸正半軸與![]() 軸正半軸上,
軸正半軸上,![]() 是對角線.點
是對角線.點![]() 從
從![]() 點出發向
點出發向![]() 點運動(不與點
點運動(不與點![]() ,
,![]() 重合),到達
重合),到達![]() 點時停止運動,射線
點時停止運動,射線![]() 交
交![]() 軸于點
軸于點![]() ,
,![]() ,
,![]() 交
交![]() 軸于點
軸于點![]() ,交
,交![]() 軸于點
軸于點![]() ,連結
,連結![]() ,
,![]() .
.
(1)求證:![]() ;
;
(2)請探究:![]() 的面積是否變化?若不變化,試求出
的面積是否變化?若不變化,試求出![]() 的面積;若變化,請說明理由;
的面積;若變化,請說明理由;
(3)當![]() 為何值時,
為何值時,![]() 是等腰直角三角形;
是等腰直角三角形;
(4)過![]() 點作
點作![]() ,垂足為點
,垂足為點![]() ,請直接寫出點
,請直接寫出點![]() 運動的路線長.
運動的路線長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,關于![]() 的二次函數
的二次函數![]() 的圖像與
的圖像與![]() 軸交于點
軸交于點![]() 和點
和點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,拋物線的對稱軸與
,拋物線的對稱軸與![]() 軸交于點
軸交于點![]() .
.
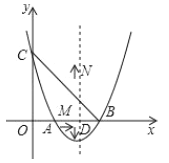
(1)求二次函數的表達式;
(2)在![]() 軸上是否存在一點
軸上是否存在一點![]() ,使
,使![]() 為等腰三角形?若存在,請求出點
為等腰三角形?若存在,請求出點![]() 的坐標;
的坐標;
(3)有一個點![]() 從點
從點![]() 出發,以每秒1個單位的速度在
出發,以每秒1個單位的速度在![]() 上向點
上向點![]() 運動,另一個點
運動,另一個點![]() 從點
從點![]() 與點
與點![]() 同時出發,以每秒2個單位的速度在拋物線的對稱軸上運動,當點
同時出發,以每秒2個單位的速度在拋物線的對稱軸上運動,當點![]() 到達點
到達點![]() 時,點
時,點![]() 、
、![]() 同時停止運動,問點
同時停止運動,問點![]() 、
、![]() 運動到何處時,
運動到何處時,![]() 面積最大,試求出最大面積.
面積最大,試求出最大面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,有一輪船在A處測得南偏東30°方向上有一小島P,輪船沿正南方向航行至B處,測得小島P在南偏東45°方向上,按原方向再航行10海里至C處,測得小島P在正東方向上,則A,B之間的距離是( )
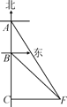
A. 10![]() 海里 B. (10
海里 B. (10![]() -10)海里
-10)海里
C. 10海里 D. (10![]() -10)海里
-10)海里
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,海上有一燈塔P,在它周圍3海里處有暗礁.一艘客輪以9海里/時的速度由西向東航行,行至A點處測得P在它的北偏東60度的方向,繼續行駛20分鐘后,到達B處又測得燈塔P在它的北偏東45度方向. 問客輪不改變方向繼續前進有無觸礁的危險?

查看答案和解析>>
科目:初中數學 來源: 題型:
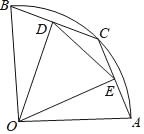
【題目】如圖,在半徑為1的扇形AOB中,∠AOB=90°,點C是弧AB上的一個動點(不與點A、B重合)OD⊥BC,OE⊥AC,垂足分別為D、E.
(1)當![]() 時,求線段OD的長;
時,求線段OD的長;
(2)在△DOE中是否存在長度保持不變的邊?如果存在,請指出是哪條邊,并求其長度;如果不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
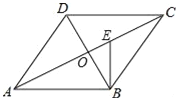
【題目】如圖,在ABCD中,對角線AC與BD相交于點O,∠CAB=∠ACB,過點B作BE⊥AB交AC于點E.
(1)求證:AC⊥BD;
(2)若AB=14,cos∠CAB=![]() ,求線段OE的長.
,求線段OE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
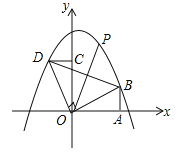
【題目】如圖,Rt△AOB的直角邊OA在x軸上,OA=2,AB=1,將Rt△AOB繞點O逆時針旋轉90°得到Rt△COD,拋物線![]() 經過B、D兩點.
經過B、D兩點.
(1)求二次函數的解析式;
(2)連接BD,點P是拋物線上一點,直線OP把△BOD的周長分成相等的兩部分,求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】足球運動員將足球沿與地面成一定角度的方向踢出,足球飛行的路線是一條拋物線,不考慮空氣阻力,足球距離地面的高度![]() (單位:
(單位:![]() )與足球被踢出后經過的時間
)與足球被踢出后經過的時間![]() (單位:
(單位:![]() )之間的關系如下表:
)之間的關系如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| 0 | 8 | 14 | 18 | 20 | 20 | 18 | 14 | … |
下列結論:①足球距離地面的最大高度為![]() ;②足球飛行路線的對稱軸是直線
;②足球飛行路線的對稱軸是直線![]() ;③足球被踢出
;③足球被踢出![]() 時落地;④足球被踢出
時落地;④足球被踢出![]() 時,距離地面的高度是
時,距離地面的高度是![]() .
.
其中正確結論的個數是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com