精品一区二区免费在线观看_国产精品久久久久久av福利软件_97成人精品区在线播放_国内成人精品一区

2.在已知一個角的三角函數值，求這個角的其他三角函數值時，要注意題設中角的范圍，并就不同的象限正確確定三角函數值的符號,求出相應的值.

1.任意角、弧度制、與角度制的互化，弧長、扇形面積公式；任意角的三角函數概念.

[例1]已知α是第二象限的角

(1) 指出α／2所在的象限，并用圖象表示其變化范圍；

(2) 若α還滿足條件|α+2|≤4，求α的取值區間;

(3) 若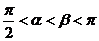,求α－β的范圍.

　 解：依題意，2kπ+π/2＜α＜2kπ+π(k∈Z)

(1) 所以kπ+π/4＜α/2＜kπ+π/2(k∈Z)，若k為偶數，則α/2是第一象限的角；若k為奇數，則α/2是第三象限的角；其變化范圍如圖中的陰影部分所示(不含邊界)

(2) 因為|α+2|≤4，所以－6≤α≤2，

即α∈(2kπ+π/2，2kπ+π)∩[－6，2]，

結合數軸可知，α∈(－3π/2，－π)∪(π/2，2。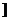

(3)

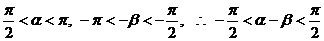
又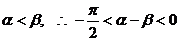

◆提煉方法: 理解象限角、終邊相同的角、區間角的概念，掌握α角的取值范圍與2α、α/2角的取值范圍間的相互關系。

[例2]化簡(1) ()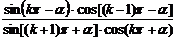

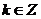　 (2);　　

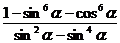(3) 若sinα·cosα＜0，sinα·tanα＜0，化簡+.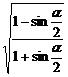

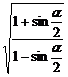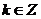　 　　解：(1)當k為偶數時，原式==－1；當k為奇數時同理可得，原式=－1，故當時，原式=-1。

　　 (2)原式=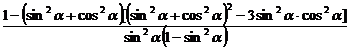=3

(3)由所給條件知α是第二象限角，則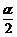是第一或第三象限角.

原式==

=

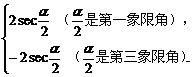
◆關鍵點注:(1)分清k的奇偶，決定函數值符號是關鍵；

(2)平方式降次是化簡的重要手段之一。

[例3](1)確定lg(cos6－sin6)的符號；

　　 (2)若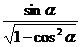+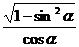=0，判斷cos(sinα)•sin(cosα)的符號。

　解：(1)∵6是第四象限的角，∴cos6＞0，sin6＜0，故cos6－sin6＞0；

∵(cos6－sin6)²=1-2sin6cos6＞1，∴cos6－sin6＞1，∴lg(cos6－sin6)＞0

(2)由題意可得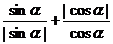=0，∴sinα•cosα＜0，故α在第二或第四象限。

①　　 若α在第二象限，則0＜sinα＜1，-1＜cosα＜0，∴cos(sinα)＞0，

sin(cosα)＜0；∴原式＜0。

②　　 若α在第四象限，則-1＜sinα＜0，0＜cosα＜1，∴cos(sinα)＞0，

sin(cosα)＞0；∴原式＞0。

　　 ◆思路方法:判斷角所在的象限是解決此類問題的關鍵。對于用弧度制表示的角不好判定所在象限時，可轉化成角度來表示。

[例4]時鐘上自7點整到分針與 時針第一次重合,求分針轉過的弧度數.如果分針長11cm,求分針轉過扇形的面積.

解:設分針轉過的弧度數的絕對值為x,則時針轉過的角的弧度數的絕對值為,由分針、時針轉過的時間相等得：(分鐘)。

分針轉過扇形的面積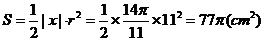

答：分針轉過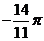，轉過扇形的面積為77πcm².

[研討.欣賞]證明：(1)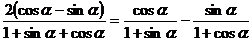

(2) 若sinα=msinβ,tanα=ntanβ,且α,β為銳角,則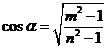

證明(1)法一：右邊=

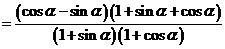
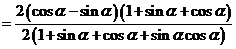
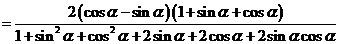
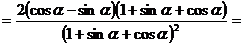左邊

法二：要證等式即證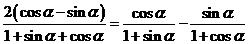

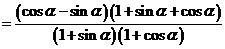
只需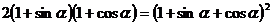證 即證

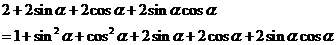
即顯然成立,所以原等式成立。

(2)(注意結論,應消去β)

由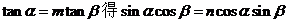　 ①

由sinα=msinβ　　 ②

得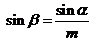,代入①得ncosα=mcosβ與②平方相加得(n²-1)cos²α=m²-1.

∵α是銳角,　 ∴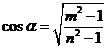

◆思維點撥：1．證等式常用方法：從一邊推另一邊；化繁為簡；左右歸一；變形論證；綜合法；比較法等.

2．常用變形技巧：切割化弦，化異為同，湊分母，“1”的代換．

6.依題意得解得a=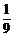或a=1(舍去).

5. ∵sin(α+β)=1，∴α+β=2kπ+.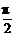

∴sin(2α+β)=sin［2(α+β)－β］=sinβ=.

4.從cosα=中可推知sinα、cotα的值，再用誘導公式即可求之.

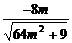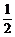3. cosα==－.∴m=或m=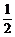－(舍去)答案：A

1.結合三角函數線知

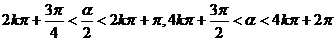α在第四象限. 答案：D

法2: sinα=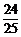－＜0，cosα= ＞0，∴α終邊在第四象限.

6. 已知sinθ=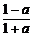，cosθ=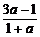，若θ是第二象限角，則實數a=______

簡答:1-3.DCA; 4. 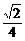; 5. ; 6. .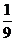

5. 已知sinβ=，sin(α+β)=1，則sin(2α+β)=_________.