
2.難點是學生有初中的知識,往往誤認為壓力N的大小總是跟滑動物體所受的重力相
等,因此必須指出只有當兩物體的接觸面垂直,物體在水平拉力作用下,沿水平面滑動時,壓力N的大小才跟物體所受的重力相等。
1.本節(jié)課的內(nèi)容分滑動摩擦力和靜摩擦力兩部分。重點是摩擦力產(chǎn)生的條件、特性和規(guī)律,通過演示實驗得出關(guān)系f=μN。
3.情感態(tài)度價值觀:
在分析物體所受摩擦力時,突出主要矛盾,忽略次要因素及無關(guān)因素,總結(jié)出摩擦力產(chǎn)生的條件和規(guī)律。
l.知識與技能:
(1)知道摩擦力產(chǎn)生的條件。
(2)能在簡單問題中,根據(jù)物體的運動狀態(tài),判斷靜摩擦力的有無、大小和方向;知道存在著最大靜摩擦力。
(3)掌握動磨擦因數(shù),會在具體問題中計算滑動磨擦力,掌握判定摩擦力方向的方法。
(4)知道影響到摩擦因數(shù)的因素。
2.過程與方法:
通過觀察演示實驗,概括出摩擦力產(chǎn)生的條件及摩擦力的特點,培養(yǎng)學生的觀察、概括能力。通過靜摩擦力與滑動摩擦力的區(qū)別對比,培養(yǎng)學生分析綜合能力。
38.(2009重慶卷文)(本小題滿分12分,(Ⅰ)問7分,(Ⅱ)問5分)
已知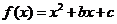 為偶函數(shù),曲線
為偶函數(shù),曲線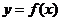 過點
過點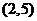 ,
,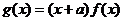 .
.
(Ⅰ)求曲線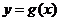 有斜率為0的切線,求實數(shù)
有斜率為0的切線,求實數(shù)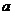 的取值范圍;
的取值范圍;
(Ⅱ)若當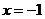 時函數(shù)
時函數(shù)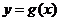 取得極值,確定
取得極值,確定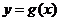 的單調(diào)區(qū)間.
的單調(diào)區(qū)間.
解: (Ⅰ)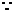
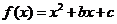 為偶函數(shù),故
為偶函數(shù),故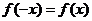 即有
即有
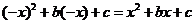 解得
解得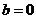
又曲線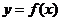 過點
過點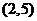 ,得
,得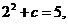 有
有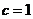
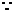
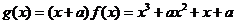 從而
從而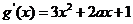 ,
,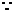 曲線
曲線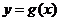 有斜率為0的切線,故有
有斜率為0的切線,故有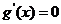 有實數(shù)解.即
有實數(shù)解.即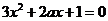 有實數(shù)解.此時有
有實數(shù)解.此時有 解得
解得
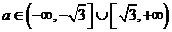 所以實數(shù)
所以實數(shù)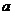 的取值范圍:
的取值范圍: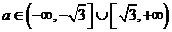
(Ⅱ)因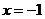 時函數(shù)
時函數(shù)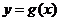 取得極值,故有
取得極值,故有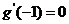 即
即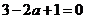 ,解得
,解得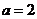
又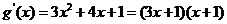 令
令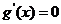 ,得
,得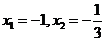
當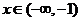 時,
時, 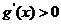 ,故
,故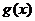 在
在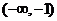 上為增函數(shù)
上為增函數(shù)
當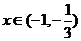 時,
時, 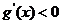 ,故
,故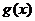 在
在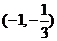 上為減函數(shù)
上為減函數(shù)
當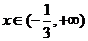 時,
時, 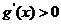 ,故
,故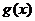 在
在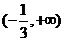 上為增函數(shù)21世紀教育網(wǎng)
上為增函數(shù)21世紀教育網(wǎng) 

37.(2009重慶卷理)(本小題滿分13分,(Ⅰ)問5分,(Ⅱ)問8分)
設(shè)函數(shù)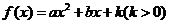 在
在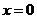 處取得極值,且曲線
處取得極值,且曲線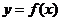 在點
在點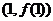 處的切線垂直于直線
處的切線垂直于直線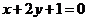 .
.
(Ⅰ)求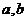 的值;
的值;
(Ⅱ)若函數(shù)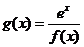 ,討論
,討論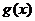 的單調(diào)性.
的單調(diào)性.
解(Ⅰ)因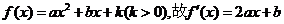
又 在x=0處取得極限值,故
在x=0處取得極限值,故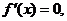 從而
從而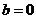 21世紀教育網(wǎng)
21世紀教育網(wǎng) 

由曲線y= 在(1,f(1))處的切線與直線
在(1,f(1))處的切線與直線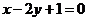 相互垂直可知
相互垂直可知
該切線斜率為2,即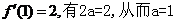
(Ⅱ)由(Ⅰ)知,
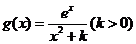
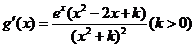
令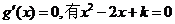
(1)當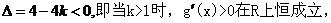
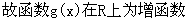
(2)當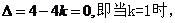
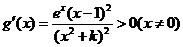
K=1時,g(x)在R上為增函數(shù)
(3)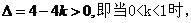 方程
方程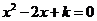 有兩個不相等實根
有兩個不相等實根
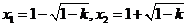 21世紀教育網(wǎng)
21世紀教育網(wǎng) 

當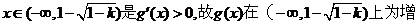 函數(shù)
函數(shù)
當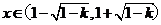 時,
時,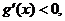 故
故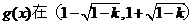 上為減函數(shù)
上為減函數(shù)
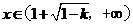 時,
時,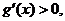 故
故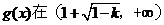 上為增函數(shù)
上為增函數(shù)
36.(2009上海卷文)(本題滿分16分)本題共有2個小題,第1小題滿分6分,第2小題滿分10分 .有時可用函數(shù)
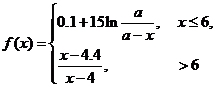
描述學習某學科知識的掌握程度.其中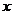 表示某學科知識的學習次數(shù)(
表示某學科知識的學習次數(shù)(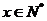 ),
),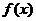 表示對該學科知識的掌握程度,正實數(shù)a與學科知識有關(guān).
表示對該學科知識的掌握程度,正實數(shù)a與學科知識有關(guān).
(1)證明:當x 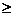 7時,掌握程度的增長量f(x+1)- f(x)總是下降;
7時,掌握程度的增長量f(x+1)- f(x)總是下降;
(2)根據(jù)經(jīng)驗,學科甲、乙、丙對應的a的取值區(qū)間分別為(115,121],(121,127],
(127,133].當學習某學科知識6次時,掌握程度是85%,請確定相應的學科.
證明(1)當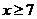 時,
時,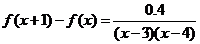
而當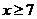 時,函數(shù)
時,函數(shù)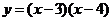 單調(diào)遞增,且
單調(diào)遞增,且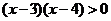
故函數(shù)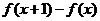 單調(diào)遞減
單調(diào)遞減
當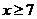 時,掌握程度的增長量
時,掌握程度的增長量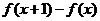 總是下降21世紀教育網(wǎng)
總是下降21世紀教育網(wǎng) 

(2)有題意可知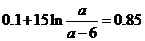
整理得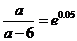
解得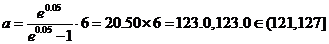 …….13分
…….13分
由此可知,該學科是乙學科……………..14分
35.(2009年上海卷理)(本題滿分16分)本題共有3個小題,第1小題滿分4分,第2小題滿分6分,第3小題滿分6分。
已知函數(shù)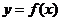 的反函數(shù)。定義:若對給定的實數(shù)
的反函數(shù)。定義:若對給定的實數(shù)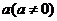 ,函數(shù)
,函數(shù)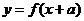 與
與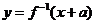 互為反函數(shù),則稱
互為反函數(shù),則稱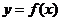 滿足“
滿足“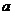 和性質(zhì)”;若函數(shù)
和性質(zhì)”;若函數(shù)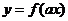 與
與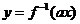 互為反函數(shù),則稱
互為反函數(shù),則稱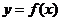 滿足“
滿足“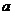 積性質(zhì)”。
積性質(zhì)”。
(1)
判斷函數(shù)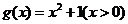 是否滿足“1和性質(zhì)”,并說明理由;
是否滿足“1和性質(zhì)”,并說明理由;
(2) 求所有滿足“2和性質(zhì)”的一次函數(shù);
(3)
設(shè)函數(shù)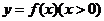 對任何
對任何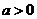 ,滿足“
,滿足“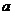 積性質(zhì)”。求
積性質(zhì)”。求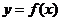 的表達式。
的表達式。
解:(1)函數(shù)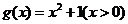 的反函數(shù)是
的反函數(shù)是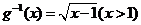
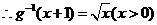
而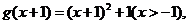 其反函數(shù)為
其反函數(shù)為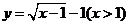
故函數(shù)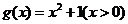 不滿足“1和性質(zhì)”
不滿足“1和性質(zhì)”
(2)設(shè)函數(shù)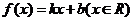 滿足“2和性質(zhì)”,
滿足“2和性質(zhì)”,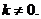
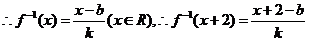 …….6分
…….6分
而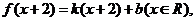 得反函數(shù)
得反函數(shù)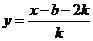 ………….8分
………….8分
由“2和性質(zhì)”定義可知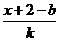 =
=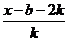 對
對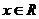 恒成立
恒成立
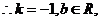 即所求一次函數(shù)為
即所求一次函數(shù)為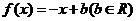 ………..10分
………..10分
(3)設(shè)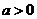 ,
,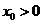 ,且點
,且點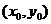 在
在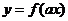 圖像上,則
圖像上,則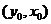 在函數(shù)
在函數(shù)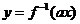 圖象上,
圖象上,
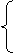 故
故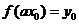 ,可得
,可得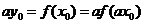 ,
......12分
,
......12分
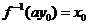 ,
,
令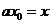 ,則
,則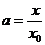 。
。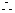
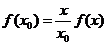 ,即
,即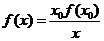 。 ......14分
。 ......14分
綜上所述,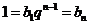
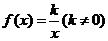 ,此時
,此時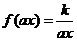 ,其反函數(shù)就是
,其反函數(shù)就是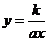 ,
,
而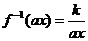 ,故
,故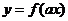 與
與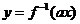 互為反函數(shù) 。
......16分
互為反函數(shù) 。
......16分
34.(2009年上海卷理)(本題滿分14分)本題共有2個小題,第1小題滿分6分,第2小題滿分8分。
有時可用函數(shù)
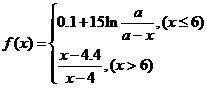
描述學習某學科知識的掌握程度,其中x表示某學科知識的學習次數(shù)(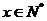 ),
), 表示對該學科知識的掌握程度,正實數(shù)a與學科知識有關(guān)。
表示對該學科知識的掌握程度,正實數(shù)a與學科知識有關(guān)。
(1)
證明:當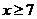 時,掌握程度的增加量
時,掌握程度的增加量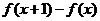 總是下降;
總是下降;
(2)
根據(jù)經(jīng)驗,學科甲、乙、丙對應的a的取值區(qū)間分別為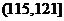 ,
,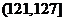 ,
,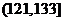 。當學習某學科知識6次時,掌握程度是85%,請確定相應的學科。
。當學習某學科知識6次時,掌握程度是85%,請確定相應的學科。
證明(1)當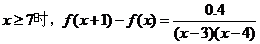
而當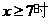 ,函數(shù)
,函數(shù)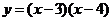 單調(diào)遞增,且
單調(diào)遞增,且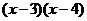 >0……..3分
>0……..3分
故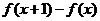 單調(diào)遞減
單調(diào)遞減
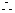 當
當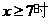 ,掌握程度的增長量
,掌握程度的增長量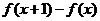 總是下降……………..6分
總是下降……………..6分
(2)由題意可知0.1+15ln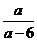 =0.85……………….9分
=0.85……………….9分
整理得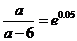
解得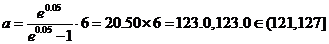 …….13分
…….13分
由此可知,該學科是乙學科……………..14分
33.(2009福建卷文)(本小題滿分12分)
已知函數(shù)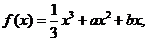 且
且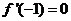
(I)試用含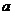 的代數(shù)式表示
的代數(shù)式表示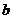 ;
;
(Ⅱ)求 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅲ)令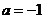 ,設(shè)函數(shù)
,設(shè)函數(shù) 在
在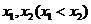 處取得極值,記點
處取得極值,記點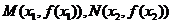 ,證明:線段
,證明:線段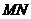 與曲線
與曲線 存在異于
存在異于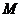 、
、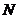 的公共點;
的公共點;
解法一:
(I)依題意,得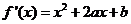
由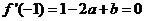 得
得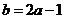
(Ⅱ)由(I)得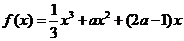 (
(
故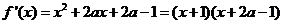
令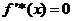 ,則
,則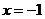 或
或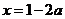
①當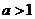 時,
時,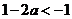
當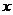 變化時,
變化時,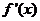 與
與 的變化情況如下表:
的變化情況如下表:
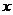 |
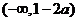 |
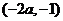 |
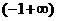 |
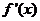 |
+ |
- |
+ |
 |
單調(diào)遞增 |
單調(diào)遞減 |
單調(diào)遞增 |
由此得,函數(shù) 的單調(diào)增區(qū)間為
的單調(diào)增區(qū)間為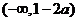 和
和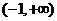 ,單調(diào)減區(qū)間為
,單調(diào)減區(qū)間為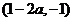
②由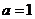 時,
時,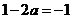 ,此時,
,此時,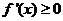 恒成立,且僅在
恒成立,且僅在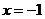 處
處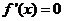 ,故函數(shù)
,故函數(shù) 的單調(diào)區(qū)間為R
的單調(diào)區(qū)間為R
③當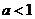 時,
時,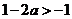 ,同理可得函數(shù)
,同理可得函數(shù) 的單調(diào)增區(qū)間為
的單調(diào)增區(qū)間為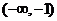 和
和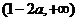 ,單調(diào)減區(qū)間為
,單調(diào)減區(qū)間為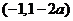
綜上:21世紀教育網(wǎng) 

當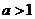 時,函數(shù)
時,函數(shù) 的單調(diào)增區(qū)間為
的單調(diào)增區(qū)間為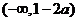 和
和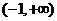 ,單調(diào)減區(qū)間為
,單調(diào)減區(qū)間為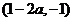 ;
;
當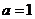 時,函數(shù)
時,函數(shù) 的單調(diào)增區(qū)間為R;
的單調(diào)增區(qū)間為R;
當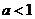 時,函數(shù)
時,函數(shù) 的單調(diào)增區(qū)間為
的單調(diào)增區(qū)間為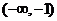 和
和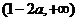 ,單調(diào)減區(qū)間為
,單調(diào)減區(qū)間為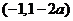
(Ⅲ)當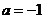 時,得
時,得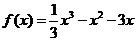
由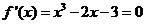 ,得
,得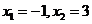
由(Ⅱ)得 的單調(diào)增區(qū)間為
的單調(diào)增區(qū)間為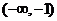 和
和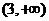 ,單調(diào)減區(qū)間為
,單調(diào)減區(qū)間為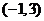
所以函數(shù) 在
在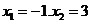 處取得極值。
處取得極值。
故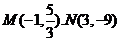
所以直線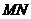 的方程為
的方程為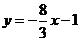
由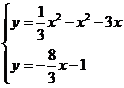 得
得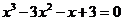
令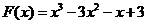
易得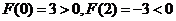 ,而
,而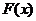 的圖像在
的圖像在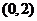 內(nèi)是一條連續(xù)不斷的曲線,
內(nèi)是一條連續(xù)不斷的曲線,
故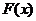 在
在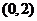 內(nèi)存在零點
內(nèi)存在零點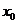 ,這表明線段
,這表明線段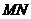 與曲線
與曲線 有異于
有異于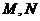 的公共點
的公共點
解法二:
(I)同解法一
(Ⅱ)同解法一。
(Ⅲ)當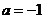 時,得
時,得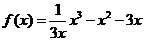 ,由
,由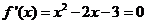 ,得
,得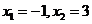
由(Ⅱ)得 的單調(diào)增區(qū)間為
的單調(diào)增區(qū)間為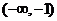 和
和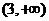 ,單調(diào)減區(qū)間為
,單調(diào)減區(qū)間為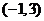 ,所以函數(shù)
,所以函數(shù) 在
在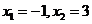 處取得極值,21世紀教育網(wǎng)
處取得極值,21世紀教育網(wǎng) 

故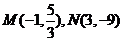
所以直線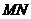 的方程為
的方程為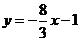
由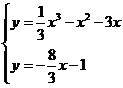 得
得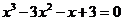
解得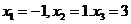
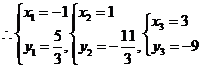
所以線段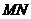 與曲線
與曲線 有異于
有異于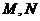 的公共點
的公共點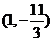
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com