
2008年杭州市各類高中招生文化考試
數學試卷
一、仔細選一選(本題有10個小題,每小題3分,共30分)
1. 北京2008奧運的國家體育場“鳥巢”建筑面積達25.8萬平方米,用科學記數法表示應為

A. 25.8×
C. 2.58×
2. 已知 是方程
是方程 的一個解,那么
的一個解,那么 的值是
的值是
A. 1
B.
3. 在直角坐標系中,點P(4, )在第一象限內,且OP與
)在第一象限內,且OP與 軸正半軸的夾角為60°,則
軸正半軸的夾角為60°,則 的值是
的值是
A.  B.
B.  C. -3 D. -1
C. -3 D. -1
4. 如圖,已知直線AB∥CD,∠C=115°,∠A=25°,則∠E=

A. 70° B. 80° C. 90° D. 100°
5. 化簡 的結果是
的結果是
A.  B.
B.  C.
C.  D.
D. 
6. 設一個銳角與這個角的補角的差的絕對值為 ,則
,則
A. 0°< <90°
B. 0°<
<90°
B. 0°< ≤90°
≤90°
C. 0°< <90°或90°<
<90°或90°< <180° D. 0°<
<180° D. 0°< <180°
<180°
7. 在一次質檢抽測中,隨機抽取某攤位20袋食鹽,測得各袋的質量分別為(單位:g)
492 496 494 495 498 497 501 502 504 496
497 503 506 508 507 492 496 500 501 499
根據以上抽測結果,任買一袋該攤位的食鹽,質量在
A. 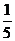 B.
B. 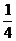 C.
C. 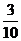 D.
D. 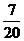
8. 由大小相同的正方體木塊堆成的幾何體的三視圖如右所示,則該幾何體中正方體木塊的個數是
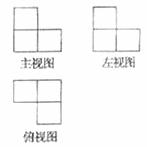
A. 6個 B. 5個
C. 4個 D. 3個
9. 以正方形ABCD的BC邊為直徑作半圓O,過點D作直線切半圓于點F,交AB邊于點E,則ΔADE和直角梯形EBCD周長之比為
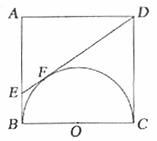
A. 3:4 B. 4:
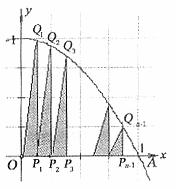
10. 如圖,記拋物線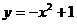 的圖象與
的圖象與 正半軸的交點為A,將線段OA分成n等份,設分點分別為P1,P2,…,Pn-1,過每個分點作
正半軸的交點為A,將線段OA分成n等份,設分點分別為P1,P2,…,Pn-1,過每個分點作 軸的垂線,分別與拋物線交于點Q1,Q2,…,Qn-1,再記直角三角形OP1Q1,P1P2Q2,…的面積分別為S1,S2,…,這樣就有
軸的垂線,分別與拋物線交于點Q1,Q2,…,Qn-1,再記直角三角形OP1Q1,P1P2Q2,…的面積分別為S1,S2,…,這樣就有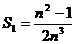 ,
, ,…;記W=S1+S2+…+Sn-1,當n越來越大時,你猜想W最接近的常數是
,…;記W=S1+S2+…+Sn-1,當n越來越大時,你猜想W最接近的常數是
A. 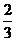 B.
B.
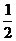 C.
C. 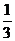 D.
D. 
二、認真填一填(本題有6個小題,每小題4分,共24分)
11. 寫出一個比-1大的負有理數是_____;比-1大的負無理數是_____
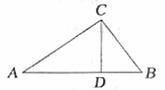
12. 如下圖,在RtΔABC中,∠C為直角,CD⊥AB于點D,BC=3,AB=5,寫出其中的一對相似三角形是__________和__________;并寫出它們的面積比_________
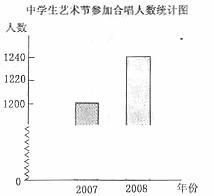
13. 小張根據某媒體上報道的一張條形統計圖(如下),在隨筆中寫道:“……今年在我市的中學生藝術節上,參加合唱比賽的人數比去年激增……”。小張說得對不對?為什么?請你用一句話對小張的說法作個評價:
14. 從1至9這9個自然數中任取一個,是2的倍數或是3的倍數的概率是________
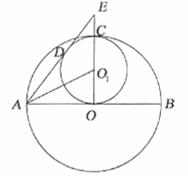
15. 如下圖,大圓O的半徑OC是小圓O1的直徑,且有OC垂直于⊙O的直徑AB。⊙O1的切線AD交OC的延長線于點E,切點為D。已知⊙O1的半徑為r,則AO1=________;DE_________
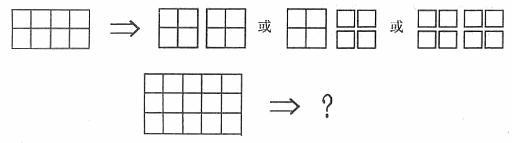
16. 如圖,一個4×2的矩形可以用3種不同的方式分割成2或5或8個小正方形,那么一個5×3的矩形用不同的方式分割后,小正方形的個數可以是__________________
解答應寫出文字說明、證明過程或推演步驟。如果覺得有的題目有點困難,那么把自己能寫出的解答寫出一部分也可以。
三、全面答一答(本題有8個小題,共66分)
17.(本小題滿分6分)
課本中介紹我國古代數學名著《孫子算經》上有這樣一道題:今有雞兔同籠,上有三十五頭,下有九十四足,問雞兔各幾頭(只)?
如果假設雞有 只,兔有
只,兔有 只,請你列出關于
只,請你列出關于 ,
, 的二元一次方程組,并寫出你求解這個方程組的方法。
的二元一次方程組,并寫出你求解這個方程組的方法。
18.(本小題滿分6分)
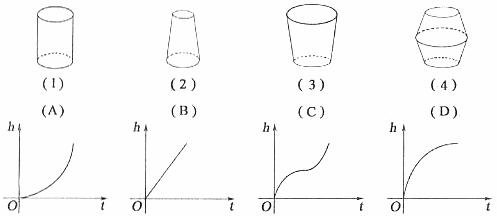
如圖,水以恒速(即單位時間內注入水的體積相同)注入下面四種底面積相同的容器中,
(1)請分別找出與各容器對應的水的高度h和時間t的函數關系圖象,用直線段連接起來;
(2)當容器中的水恰好達到一半高度時,請在各函數關系圖的t軸上標出此時t值對應點T的位置。
19.(本小題滿分6分)
在凸多邊形中,四邊形有2條對角線,五邊形有5條對角線,經過觀察、歸納,你認為凸八邊形的對角線條數應該是多少條?簡單扼要地寫出你的思考過程。
20.(本小題滿分8分)
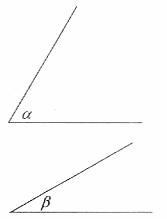
如下圖,已知∠α,∠β,用直尺和圓規求作一個∠γ,使得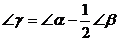
(只須做出正確圖形,保留作圖痕跡,不必寫出作法)
21.(本小題滿分8分)
據
年度
2000
2001
2002
2003
2004
2005
2006
汽車總數
70
90
105
135
170
私人汽車
25
30
75
135
175
私人汽車占總量比例
35.7%
33.3%
55.6%
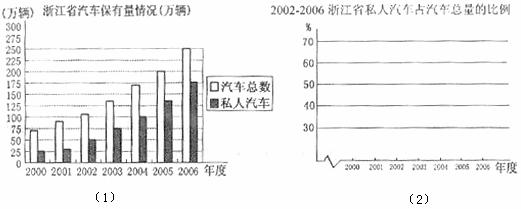
(1)請你根據圖1直方圖提供的信息將上表補全;
(2)請在下面圖2中將私人汽車占汽車總量的比例用折線圖表示出來
22.(本小題滿分10分)
為了預防流感,某學校在休息天用藥熏消毒法對教室進行消毒。已知藥物釋放過程中,室內每立方米空氣中含藥量y(毫克)與時間t(小時)成正比;藥物釋放完畢后,y與t的函數關系為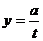 (
( 為常數)。如下圖所示,據圖中提供的信息,解答下列問題:
為常數)。如下圖所示,據圖中提供的信息,解答下列問題:
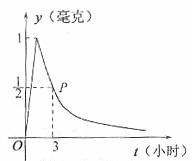
(1)寫出從藥物釋放開始,y與t之間的兩個函數關系式及相應的自變量取值范圍;
(2)據測定,當空氣中每立方米和含藥量降低到0.25毫克以下時,學生方可進入教室,那么從藥物釋放開始,至少需要經過多少小時后,學生才能進入教室?
23.(本小題滿分10分)
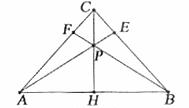
如下圖,在等腰ΔABC中,CH是底邊上的高線,點P是線段CH上不與端點重合的任意一點,連結AP交BC于點E,連結BP交AC于點F。
(1)證明:∠CAE=∠CBF;
(2)證明:AE=BF;
(3)以線段AE,BF和AB為邊構成一個新的三角形ABG(點E與點F重合于點G),記ΔABC和ΔABG的面積分別為SΔABC和SΔABG,如果存在點P,能使SΔABC=SΔABG,求∠C的取值范圍。
24.(本小題滿分12分)
在直角坐標系xOy中,設點A(0,t),點Q(t,b)。平移二次函數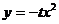 的圖象,得到的拋物線F滿足兩個條件:①頂點為Q;②與x軸相交于B,C兩點(ㄏOBㄏ<ㄏOCㄏ),連結A,B。
的圖象,得到的拋物線F滿足兩個條件:①頂點為Q;②與x軸相交于B,C兩點(ㄏOBㄏ<ㄏOCㄏ),連結A,B。
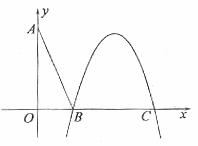
(1)是否存在這樣的拋物線F,使得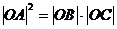 ?請你做出判斷,并說明理由;
?請你做出判斷,并說明理由;
(2)如果AQ∥BC,且tan∠ABO=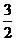 ,求拋物線F對應的二次函數的解析式。
,求拋物線F對應的二次函數的解析式。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com