
科目:高中數學 來源: 題型:解答題
已知函數f (x)=x 2+ax ,且對任意的實數x都有f (1+x)=f (1-x) 成立.
(1)求實數 a的值; (2)利用單調性的定義證明函數f(x)在區間[1,+∞
(2)利用單調性的定義證明函數f(x)在區間[1,+∞ 上是增函數.
上是增函數.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(12分)已知二次函數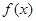 的最小值為1,且
的最小值為1,且 .
.
(1)求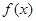 的解析式;
的解析式;
(2)若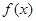 在區間
在區間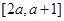 上不單調,求實數
上不單調,求實數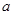 的取值范圍;
的取值范圍;
(3)在區間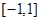 上,
上,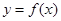 的圖象恒在
的圖象恒在 的圖象上方,試確定實數
的圖象上方,試確定實數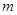 的
的 取值范圍。
取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)已知定義域為R的函數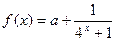 是奇函數.
是奇函數.
(Ⅰ)求 a的值,并指出函數
a的值,并指出函數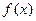 的單調性(不必說明單調性理
的單調性(不必說明單調性理 由);
由);
(Ⅱ)若對任意的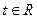 ,不等式
,不等式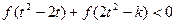 恒成立,求
恒成立,求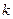 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分) 設a > 1,函數 .
.
(1)求 的反函數
的反函數 ;
;
(2)若 在[0,1]上的最大值與最小值互為相反數,求a的值;
在[0,1]上的最大值與最小值互為相反數,求a的值;
(3)若 的圖象不經過第二象限,求a的取值范圍.
的圖象不經過第二象限,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數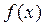 =ax2+(b-8)x-a-ab , 當x
=ax2+(b-8)x-a-ab , 當x (-∞,-3)
(-∞,-3) (2,+∞)時,
(2,+∞)時, 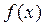 <0,當x
<0,當x (-3,2)時
(-3,2)時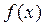 >0 .
>0 .
(1)求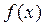 在[0,1]內的值域.
在[0,1]內的值域.
(2)若ax2+bx+c≤0的解集為R,求實數c的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題12分)如圖,函數y= |x|在x∈[-1,1]的圖象上有兩點A、B,
|x|在x∈[-1,1]的圖象上有兩點A、B, AB∥
AB∥
Ox軸,點M(1,m)(m是已知實數,且m> )是△ABC的邊BC的中點。
)是△ABC的邊BC的中點。
(Ⅰ)寫出用B的橫坐標t表示△ABC面積S的函數解析式S=f(t);
(Ⅱ)求函數S=f(t)的最大值,并求出相應的C點坐標。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com