
某企業擬建造如圖所示的容器(不計厚度,長度單位:米),其中容器的中間為圓柱形,左右兩端均為半球形,按照設計要求容器的容積為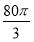 立方米,且l≥2r.假設該容器的建造費用僅與其表面積有關,已知圓柱形部分每平方米建造費用為3千元,半球形部分每平方米建造費用為c(c>3)千元.設該容器的建造費用為y千元.
立方米,且l≥2r.假設該容器的建造費用僅與其表面積有關,已知圓柱形部分每平方米建造費用為3千元,半球形部分每平方米建造費用為c(c>3)千元.設該容器的建造費用為y千元.
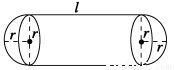
①寫出y關于r的函數表達式,并求該函數的定義域;
②求該容器的建造費用最小時的r.
①y=4π(c-2)r2+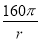 ,0<r≤2②當3<c≤
,0<r≤2②當3<c≤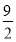 時,建造費用最小時r=2;當c>
時,建造費用最小時r=2;當c>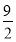 時,建造費用最小時,r=
時,建造費用最小時,r= 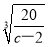 .
.
【解析】①設容器的容積為V,
由題意知V=πr2l+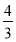 πr3,又V=
πr3,又V=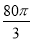 ,
,
∴l= .
.
由于l≥2r,∴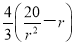 ≥2r,∴0<r≤2.
≥2r,∴0<r≤2.
所以建造費用y=2πrl×3+4πr2c=2πr×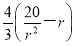 ×3+4πr2c
×3+4πr2c
因此,y=4π(c-2)r2+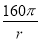 ,0<r≤2.
,0<r≤2.
②由①知y′=8π(c-2)r-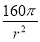 =
=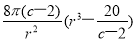 ,
,
由于c>3,
∴c-2>0.由y′=0得r= 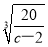
若0< 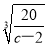 <2,即c>
<2,即c>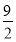 時,此時0<r<
時,此時0<r< 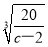 時,y′<0,
時,y′<0,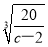 <r<2時,y′>0.
<r<2時,y′>0.
∴r=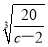 時,y取得極小值.
時,y取得極小值.
若 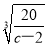 ≥2,即3<c≤
≥2,即3<c≤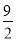 時,0<r<2時,y′<0,函數單調遞減,
時,0<r<2時,y′<0,函數單調遞減,
∴r=2時,y取得極小值.
總之,當3<c≤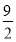 時,建造費用最小時r=2;
時,建造費用最小時r=2;
當c>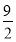 時,建造費用最小時,r=
時,建造費用最小時,r= 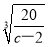 .
.


 三新快車金牌周周練系列答案
三新快車金牌周周練系列答案科目:高中數學 來源:2015屆湘教版高二數學選修2-2基礎達標5章末練習卷(解析版) 題型:選擇題
已知z是純虛數,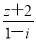 是實數,那么z等于 ( ).
是實數,那么z等于 ( ).
A.2i B.i C.-i D.-2i
查看答案和解析>>
科目:高中數學 來源:2015屆湘教版高二數學選修2-2基礎達標4章末練習卷(解析版) 題型:填空題
若曲線f(x)=ax3+ln x存在垂直于y軸的切線,則實數a的取值范圍是
________.
查看答案和解析>>
科目:高中數學 來源:2015屆湘教版高二數學選修2-2基礎達標4.5練習卷(解析版) 題型:填空題
f(x)是一次函數,且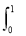 f(x)dx=5,
f(x)dx=5,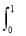 xf(x)dx=
xf(x)dx=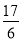 ,那么f(x)的解析式是________.
,那么f(x)的解析式是________.
查看答案和解析>>
科目:高中數學 來源:2015屆湘教版高二數學選修2-2基礎達標4.5練習卷(解析版) 題型:解答題
設力F作用在質點m上使m沿x軸從x=1運動到x=10,已知F=x2+1且力的方向和x軸的正向相同,求F對質點m所作的功.
查看答案和解析>>
科目:高中數學 來源:2015屆湘教版高二數學選修2-2基礎達標4.4練習卷(解析版) 題型:選擇題
某車間分批生產某種產品,每批的生產準備費用為800元,若每批生產x件,則平均倉儲時間為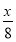 天,且每件產品每天的倉儲費用為1元.為使平均到每件產品的生產準備費用與倉儲費用之和最小,每批應生產產品 ( ).
天,且每件產品每天的倉儲費用為1元.為使平均到每件產品的生產準備費用與倉儲費用之和最小,每批應生產產品 ( ).
A.60件 B.80件
C.100件 D.120件
查看答案和解析>>
科目:高中數學 來源:2015屆湘教版高二數學選修2-2基礎達標4.3練習卷(解析版) 題型:解答題
已知函數f(x)=4x3+3tx2-6t2x+t-1,x∈R,其
中t∈R.
①當t=1時,求曲線y=f(x)在點(0,f(0))處的切線方程;
②當t≠0時,求f(x)的單調區間.
查看答案和解析>>
科目:高中數學 來源:2015屆湘教版高二數學選修2-2基礎達標4.3練習卷(解析版) 題型:選擇題
函數y=1+3x-x3有 ( ).
A.極小值-1,極大值1 B.極小值-2,極大值3
C.極小值-2,極大值2 D.極小值-1,極大值3
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com