
【題目】已知曲線![]() 的方程為
的方程為![]() .
.
(1)當![]() 時,試確定曲線
時,試確定曲線![]() 的形狀及其焦點坐標;
的形狀及其焦點坐標;
(2)若直線![]() 交曲線
交曲線![]() 于點
于點![]() 、
、![]() ,線段
,線段![]() 中點的橫坐標為
中點的橫坐標為![]() ,試問此時曲線
,試問此時曲線![]() 上是否存在不同的兩點
上是否存在不同的兩點![]() 、
、![]() 關于直線
關于直線![]() 對稱?
對稱?
(3)當![]() 為大于1的常數時,設
為大于1的常數時,設![]() 是曲線
是曲線![]() 上的一點,過點
上的一點,過點![]() 作一條斜率為
作一條斜率為![]() 的直線
的直線![]() ,又設
,又設![]() 為原點到直線
為原點到直線![]() 的距離,
的距離,![]() 分別為點
分別為點![]() 與曲線
與曲線![]() 兩焦點的距離,求證
兩焦點的距離,求證![]() 是一個定值,并求出該定值.
是一個定值,并求出該定值.
【答案】(1) 曲線![]() 是焦點在
是焦點在![]() 軸上的橢圓,焦點坐標為
軸上的橢圓,焦點坐標為![]() ; (2) 見解析;(3)見證明
; (2) 見解析;(3)見證明
【解析】
(1)將a代入,兩邊平方并化簡,可得曲線C的方程及形狀;
(2)將![]() 代入曲線,利用PQ中點的橫坐標為
代入曲線,利用PQ中點的橫坐標為![]() ,求出m,驗證判別式是否成立,可得結論.
,求出m,驗證判別式是否成立,可得結論.
(3)將曲線C化簡,得到焦點坐標,求得![]() ,再求得點到直線
,再求得點到直線![]() 的距離,代入
的距離,代入![]() 化簡得到定值.
化簡得到定值.
(1)當![]() 時,
時,![]() ,兩邊平方并化簡得
,兩邊平方并化簡得![]() ,
,
∴曲線![]() 是焦點在
是焦點在![]() 軸上的橢圓,其長半軸長為1,短半軸長為
軸上的橢圓,其長半軸長為1,短半軸長為![]() ,焦點坐標為
,焦點坐標為![]() ;
;
(2)將![]() 代入
代入![]() ,消去
,消去![]() ,
,
得![]() ,由題意,
,由題意,![]() ,
,
即![]() ,解得
,解得![]() 或
或![]() (舍),此時,
(舍),此時,![]() ,
,![]() ,
,
設![]() ,
,![]() ,
,![]() ,
,
將![]() 代入
代入![]() ,得
,得![]() ,則
,則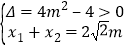 ,
,
![]() 的中點坐標為
的中點坐標為![]() 在對稱軸
在對稱軸![]() 上,∴
上,∴![]() ,解得
,解得![]() ,
,
不滿足![]() ,∴曲線
,∴曲線![]() 上不存在不同的兩點
上不存在不同的兩點![]() 、
、![]() 關于直線
關于直線![]() 對稱;
對稱;
(3)![]() ,兩焦點坐標為
,兩焦點坐標為![]() 、
、![]() ,
,![]() ,
,
![]() ,即
,即![]() ,
,
∴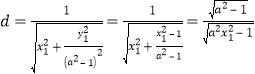 ,
,
用![]() 替換
替換![]() 中的
中的![]() ,
,
可得![]() ,∴
,∴![]() ,
,
∴![]() .
.


 永乾教育寒假作業快樂假期延邊人民出版社系列答案
永乾教育寒假作業快樂假期延邊人民出版社系列答案科目:高中數學 來源: 題型:
【題目】有下列四個命題:
(1)“若![]() ,則
,則![]() ,
,![]() 互為倒數”的逆命題;
互為倒數”的逆命題;
(2)“面積相等的三角形全等”的否命題;
(3)“若![]() ,則
,則![]() 無實數解”的否命題;
無實數解”的否命題;
(4)命題:“空間中到一個正四面體的六條棱所在的直線距離均相等的點有且只有![]() 個”; 其中真命題( )
個”; 其中真命題( )
A.(1)(2)B.(2)(3)C.(1)(2)(3)D.(1)(2)(4)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有下列說法:
①一支田徑隊有男女運動員98人,其中男運動員有56人.按男、女比例用分層抽樣的方法,從全體運動員中抽出一個容量為28的樣本,那么應抽取女運動員人數是12人;
②在某項測量中,測量結果X服從正態分布N(1,σ2)(σ>0),若X在(0,1)內取值的概率為0.4,則X在(0,2)內取值的概率為0.8.
③廢品率x%和每噸生鐵成本y(元)之間的回歸直線方程為![]() 2x+256,這表明廢品率每增加1%,生鐵成本大約增加258元;
2x+256,這表明廢品率每增加1%,生鐵成本大約增加258元;
④為了檢驗某種血清預防感冒的作用,把500名未使用血清和使用血清的人一年中的感冒記錄作比較,提出假設H0:“這種血清不能起到預防作用”,利用2×2列聯表計算得K2的觀測值k≈3.918,經查對臨界值表知P(K2≥3841)≈0.05,由此,得出以下判斷:在犯錯誤的概率不超過0.05的前提下認為“這種血清能起到預防的作用”,
正確的有( )
A.①②④B.①②③C.①③D.③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司生產某種產品,一條流水線年產量為![]() 件,該生產線分為兩段,流水線第一段生產的半成品的質量指標會影響第二段生產成品的等級,具體見下表:
件,該生產線分為兩段,流水線第一段生產的半成品的質量指標會影響第二段生產成品的等級,具體見下表:
第一段生產的半成品質量指標 |
|
|
|
第二段生產的成品為一等品概率 | 0.2 | 0.4 | 0.6 |
第二段生產的成品為二等品概率 | 0.3 | 0.3 | 0.3 |
第二段生產的成品為三等品概率 | 0.5 | 0.3 | 0.1 |
從第一道生產工序抽樣調查了![]() 件,得到頻率分布直方圖如圖:
件,得到頻率分布直方圖如圖:

若生產一件一等品、二等品、三等品的利潤分別是![]() 元、
元、![]() 元、
元、![]() 元.
元.
(Ⅰ)以各組的中間值估計為該組半成品的質量指標,估算流水線第一段生產的半成品質量指標的平均值;
(Ⅱ)將頻率估計為概率,試估算一條流水線一年能為該公司創造的利潤;
(Ⅲ)現在市面上有一種設備可以安裝到流水線第一段,價格是![]() 萬元,使用壽命是
萬元,使用壽命是![]() 年,安裝這種設備后,流水線第一段半成品的質量指標服從正態分布
年,安裝這種設備后,流水線第一段半成品的質量指標服從正態分布![]() ,且不影響產量.請你幫該公司作出決策,是否要購買該設備?說明理由.
,且不影響產量.請你幫該公司作出決策,是否要購買該設備?說明理由.
(參考數據:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下表是![]() 年
年![]() 個重點城市(序號
個重點城市(序號![]() 為一線城市,其它為非一線城市)的月平均收入與房價對照表,根據表中數據并適當修正,得到房價中位數與月平均收入的線性回歸方程是
為一線城市,其它為非一線城市)的月平均收入與房價對照表,根據表中數據并適當修正,得到房價中位數與月平均收入的線性回歸方程是![]() ,我們把根據房價與月平均收入的線性回歸方程得到的房價稱為參考房價,若實際房價中位數大于參考房價,我們稱這個城市是“房價偏貴城市”.
,我們把根據房價與月平均收入的線性回歸方程得到的房價稱為參考房價,若實際房價中位數大于參考房價,我們稱這個城市是“房價偏貴城市”.
序號 | 月評價收入 | 房價中位數 | 參考房價 | 序號 | 月評價收入 | 房價中位數 | 參考房價 | 序號 | 月評價收入 | 房價中位數 | 參考房價 |
1 | 10670 | 67822 | 11 | 7081 | 17327 | 25704 | 21 | 7081 | 14792 | 15972 | |
2 | 10015 | 52584 | 51180 | 12 | 7065 | 13918 | 19476 | 22 | 7065 | 18741 | 15780 |
3 | 9561 | 50900 | 45732 | 13 | 7027 | 16286 | 19404 | 23 | 7027 | 10538 | 15324 |
4 | 8798 | 30729 | 36576 | 14 | 6974 | 16667 | 18204 | 24 | 6974 | 12069 | 14688 |
5 | 7424 | 10926 | 20088 | 15 | 6920 | 9743 | 17760 | 25 | 6920 | 2333 | 14040 |
6 | 7825 | 26714 | 24900 | 16 | 6903 | 10627 | 18120 | 26 | 6903 | 13582 | 13836 |
7 | 7770 | 39723 | 24240 | 17 | 6884 | 29000 | 17388 | 27 | 6884 | 22126 | 13608 |
8 | 7750 | 15114 | 24000 | 18 | 6654 | 7979 | 16584 | 28 | 6654 | 12207 | 10848 |
9 | 7723 | 17727 | 23676 | 19 | 6648 | 12500 | 16920 | 29 | 6648 | 12472 | 10776 |
10 | 7635 | 13012 | 22620 | 20 | 6608 | 12298 | 16200 | 30 | 6608 | 16406 | 10286 |
(1)計算城市![]() 的參考房價;
的參考房價;
(2)從![]() 個一線城市中隨機選取
個一線城市中隨機選取![]() 個城市進行調研,求恰好選到一個“房價偏貴城市”的概率;
個城市進行調研,求恰好選到一個“房價偏貴城市”的概率;
(3)完成下面的![]() 列聯表,并判斷是否有
列聯表,并判斷是否有![]() 的把握認為一線城市與該城市為“房價偏貴城市”有關?
的把握認為一線城市與該城市為“房價偏貴城市”有關?
一般城市 | 非一線城市 | 總計 | |
房價偏貴城市 | |||
不是房價偏貴城市 | |||
總計 |
附參考公式及數據:![]() ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.01 |
| 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
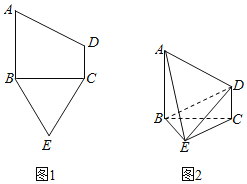
【題目】已知五邊形ABECD有一個直角梯形ABCD與一個等邊三角形BCE構成,如圖1所示,![]() ,且
,且![]() ,將梯形ABCD沿著BC折起,形成如圖2所示的幾何體,且
,將梯形ABCD沿著BC折起,形成如圖2所示的幾何體,且![]() 平面BEC.
平面BEC.
![]() 求證:平面
求證:平面![]() 平面ADE;
平面ADE;
![]() 求二面角
求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=1,AC=CD=DA=2,動點M在邊DC上(不同于D點),P為邊AB上任意一點,沿AM將△ADM翻折成△AD'M,當平面AD'M垂直于平面ABC時,線段PD'長度的最小值為_____.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com