
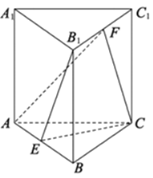
【題目】如圖,在正三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點.
的中點.
(1)求證:![]() 平面
平面![]() ;
;
(2)求平面![]() 與平面
與平面![]() 所成二面角
所成二面角![]() 銳角
銳角![]() 的余弦值.
的余弦值.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學 來源: 題型:
【題目】2019年10月1日,慶祝中華人民共和國成立70周年大會、閱兵式、群眾游行在北京隆重舉行,這次閱兵編59個方(梯)隊和聯(lián)合軍樂團,總規(guī)模約1.5萬人,各型飛機160余架、裝備580余套,是近幾次閱兵中規(guī)模最大的一次.某機構統(tǒng)計了觀看此次閱兵的年齡在30歲至80歲之間的100個觀眾,按年齡分組:第1組![]() ,第2組
,第2組![]() ,第3組
,第3組![]() ,第4組
,第4組![]() ,第5組
,第5組![]() ,得到的頻率分布直方圖如圖所示.
,得到的頻率分布直方圖如圖所示.

(1)求![]() 的值及這100個人的平均年齡(同一組中的數(shù)據(jù)用該組區(qū)間的中點值為代表);
的值及這100個人的平均年齡(同一組中的數(shù)據(jù)用該組區(qū)間的中點值為代表);
(2)用分層抽樣的方法在年齡為![]() 、
、![]() 的人中抽取5人,再從抽取的5人中隨機抽取2人接受采訪,求接受采訪的2人中年齡在
的人中抽取5人,再從抽取的5人中隨機抽取2人接受采訪,求接受采訪的2人中年齡在![]() 的恰有1人的概率.
的恰有1人的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】2019年國際籃聯(lián)籃球世界杯,將于2019年在的北京、廣州、南京、上海、武漢、深圳、佛山、東莞八座城市舉行.為了宣傳世界杯,某大學從全校學生中隨機抽取了![]() 名學生,對是否收看籃球世界杯賽事的情況進行了問卷調查,統(tǒng)計數(shù)據(jù)如下:
名學生,對是否收看籃球世界杯賽事的情況進行了問卷調查,統(tǒng)計數(shù)據(jù)如下:
會收看 | 不會收看 | |
男生 | 60 | 20 |
女生 | 20 | 20 |
(1)根據(jù)上表說明,能否有![]() 的把握認為收看籃球世界杯賽事與性別有關?
的把握認為收看籃球世界杯賽事與性別有關?
(2)現(xiàn)從參與問卷調查且收看籃球世界杯賽事的學生中,采用按性別分層抽樣的方法選取![]() 人參加2019年國際籃聯(lián)籃球世界杯賽志愿者宣傳活動.
人參加2019年國際籃聯(lián)籃球世界杯賽志愿者宣傳活動.
(i)求男、女學生各選取多少人;
(ii)若從這![]() 人中隨機選取
人中隨機選取![]() 人到校廣播站開展2019年國際籃聯(lián)籃球世界杯賽宣傳介紹,求恰好選到
人到校廣播站開展2019年國際籃聯(lián)籃球世界杯賽宣傳介紹,求恰好選到![]() 名男生的概率.
名男生的概率.
附: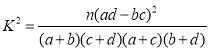 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】3月底,我國新冠肺炎疫情得到有效防控,但海外確診病例卻持續(xù)暴增,防疫物資供不應求,某醫(yī)療器械廠開足馬力,日夜生產(chǎn)防疫所需物品.已知該廠有兩條不同生產(chǎn)線![]() 和
和![]() 生產(chǎn)同一種產(chǎn)品各10萬件,為保證質量,現(xiàn)從各自生產(chǎn)的產(chǎn)品中分別隨機抽取20件,進行品質鑒定,鑒定成績的莖葉圖如下所示:
生產(chǎn)同一種產(chǎn)品各10萬件,為保證質量,現(xiàn)從各自生產(chǎn)的產(chǎn)品中分別隨機抽取20件,進行品質鑒定,鑒定成績的莖葉圖如下所示:
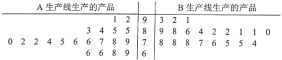
該產(chǎn)品的質量評價標準規(guī)定:鑒定成績達到![]() 的產(chǎn)品,質量等級為優(yōu)秀;鑒定成績達到
的產(chǎn)品,質量等級為優(yōu)秀;鑒定成績達到![]() 的產(chǎn)品,質量等級為良好;鑒定成績達到
的產(chǎn)品,質量等級為良好;鑒定成績達到![]() 的產(chǎn)品,質量等級為合格.將這組數(shù)據(jù)的頻率視為整批產(chǎn)品的概率.
的產(chǎn)品,質量等級為合格.將這組數(shù)據(jù)的頻率視為整批產(chǎn)品的概率.
(1)從等級為優(yōu)秀的樣本中隨機抽取兩件,記![]() 為來自
為來自![]() 機器生產(chǎn)的產(chǎn)品數(shù)量,寫出
機器生產(chǎn)的產(chǎn)品數(shù)量,寫出![]() 的分布列,并求
的分布列,并求![]() 的數(shù)學期望;
的數(shù)學期望;
(2)請完成下面質量等級與生產(chǎn)線產(chǎn)品列聯(lián)表,并判斷能不能在誤差不超過0.05的情況下,認為產(chǎn)品等級是否達到良好以上與生產(chǎn)產(chǎn)品的生產(chǎn)線有關.
|
| 合計 | |
良好以上 | |||
合格 | |||
合計 |
附: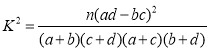
| 0.10 | 0.05 | 0.01 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】為了解高中生作文成績與課外閱讀量之間的關系,某研究機構隨機抽取了100名高中生,根據(jù)問卷調查,得到以下數(shù)據(jù):
作文成績優(yōu)秀 | 作文成績一般 | 總計 | |
課外閱讀量較大 | 35 | 20 | 55 |
課外閱讀量一般 | 15 | 30 | 45 |
總計 | 50 | 50 | 100 |
(1)根據(jù)列聯(lián)表,能否有99.5%的把握認為課外閱讀量的大小與作文成績優(yōu)秀有關;
(2)若用分層抽樣的方式從課外閱讀量一般的高中生中選取了6名高中生,再從這6名高中生中隨機選取2名進行面談,求面談的高中生中至少有1名作文成績優(yōu)秀的概率.
附: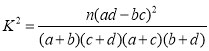 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】對稱軸為坐標軸的橢圓![]() 的焦點為
的焦點為![]() ,
,![]() ,
,![]() 在
在![]() 上.
上.
(1)求橢圓![]() 的方程;
的方程;
(2)設不過原點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
,![]() 兩點,且直線
兩點,且直線![]() ,
,![]() ,
,![]() 的斜率依次成等比數(shù)列,則當
的斜率依次成等比數(shù)列,則當![]() 的面積為
的面積為![]() 時,求直線
時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】端午節(jié)(每年農(nóng)歷五月初五),是中國傳統(tǒng)節(jié)日,有吃粽子的習俗.某超市在端午節(jié)這一天,每售出![]() kg粽子獲利潤
kg粽子獲利潤![]() 元,未售出的粽子每
元,未售出的粽子每![]() kg虧損
kg虧損![]() 元.根據(jù)歷史資料,得到銷售情況與市場需求量的頻率分布表,如下表所示.該超市為今年的端午節(jié)預購進了
元.根據(jù)歷史資料,得到銷售情況與市場需求量的頻率分布表,如下表所示.該超市為今年的端午節(jié)預購進了![]() kg粽子.以
kg粽子.以![]() (單位:kg,
(單位:kg,![]() )表示今年的市場需求量,
)表示今年的市場需求量,![]() (單位:元)表示今年的利潤.
(單位:元)表示今年的利潤.
市場需求量(kg) |
|
|
|
|
|
頻率 | 0.1 | 0.2 | 0.3 | 0.25 | 0.15 |
(1)將![]() 表示為
表示為![]() 的函數(shù);
的函數(shù);
(2)在頻率分布表的市場需求量分組中,以各組的區(qū)間中間值代表該組的各個值,需求量落入該區(qū)間的頻率作為需求量取該區(qū)間中間值的概率(例如:若需求量![]() ,則取
,則取![]() ,且
,且![]() 的概率等于需求量落入
的概率等于需求量落入![]() 的頻率
的頻率![]() ),求
),求![]() 的數(shù)學期望.
的數(shù)學期望.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設拋物線C:![]() (
(![]() )的焦點為F,經(jīng)過點F的動直線l交拋物線C于
)的焦點為F,經(jīng)過點F的動直線l交拋物線C于![]() ,
,![]() 兩點,且
兩點,且![]() .
.
(1)求拋物線C的方程;
(2)若![]() (O為坐標原點),且點E在拋物線C上,求直線l的傾斜角;
(O為坐標原點),且點E在拋物線C上,求直線l的傾斜角;
(3)若點M是拋物線C的準線上的一點,直線![]() ,
,![]() ,
,![]() 斜率分別為
斜率分別為![]() ,
,![]() ,
,![]() ,求證:當
,求證:當![]() 為定值時,
為定值時,![]() 也為定值.
也為定值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某地為改善旅游環(huán)境進行景點改造.如圖,將兩條平行觀光道l1和l2通過一段拋物線形狀的棧道AB連通(道路不計寬度),l1和l2所在直線的距離為0.5(百米),對岸堤岸線l3平行于觀光道且與l2相距1.5(百米)(其中A為拋物線的頂點,拋物線的對稱軸垂直于l3,且交l3于M),在堤岸線l3上的E,F兩處建造建筑物,其中E,F到M的距離為1(百米),且F恰在B的正對岸(即BF⊥l3).
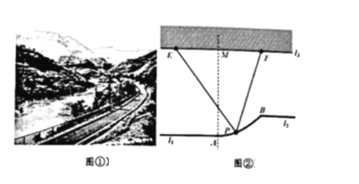
(1)在圖②中建立適當?shù)钠矫嬷苯亲鴺讼担⑶髼5?/span>AB的方程;
(2)游客(視為點P)在棧道AB的何處時,觀測EF的視角(∠EPF)最大?請在(1)的坐標系中,寫出觀測點P的坐標.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com