
【題目】已知橢圓![]() 長軸的兩個端點分別為
長軸的兩個端點分別為![]() ,
,![]() , 離心率
, 離心率![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)作一條垂直于![]() 軸的直線,使之與橢圓
軸的直線,使之與橢圓![]() 在第一象限相交于點
在第一象限相交于點![]() ,在第四象限相交于點
,在第四象限相交于點![]() ,若直線
,若直線![]() 與直線
與直線![]() 相交于點
相交于點![]() ,且直線
,且直線![]() 的斜率大于
的斜率大于![]() ,求直線
,求直線![]() 的斜率
的斜率![]() 的取值范圍.
的取值范圍.
科目:高中數學 來源: 題型:
【題目】市政府為了節約用水,調查了100位居民某年的月均用水量(單位:![]() ),頻數分布如下:
),頻數分布如下:
分組 |
|
|
|
|
|
|
|
|
|
頻數 | 4 | 8 | 15 | 22 | 25 | 14 | 6 | 4 | 2 |

(1)根據所給數據將頻率分布直圖補充完整(不必說明理由);
(2)根據頻率分布直方圖估計本市居民月均用水量的中位數;
(3)根據頻率分布直方圖估計本市居民月均用水量的平均數(同一組數據由該組區間的中點值作為代表).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線l1:x+my+1=0和l2:(m-3)x-2y+(13-7m)=0.
(1)若l1⊥l2,求實數m的值;
(2)若l1∥l2,求l1與l2之間的距離d.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若直線![]() 與x軸,y軸的交點分別為A,B,圓C以線段AB為直徑.
與x軸,y軸的交點分別為A,B,圓C以線段AB為直徑.
(1)求圓C的標準方程;
(2)若直線l過點![]() 且圓心C到l的距離為1,求直線l的方程.
且圓心C到l的距離為1,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】命題![]() :方程
:方程![]() 表示焦點在
表示焦點在![]() 軸上的雙曲線:命題
軸上的雙曲線:命題![]() :若存在
:若存在![]() ,使得
,使得![]() 成立.
成立.
(1)如果命題![]() 是真命題,求實數
是真命題,求實數![]() 的取值范圍;
的取值范圍;
(2)如果“![]() ”為假命題,“
”為假命題,“![]() ”為真命題,求實數
”為真命題,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】共享單車是指由企業在校園、公交站點、商業區、公共服務區等場所提供的自行車單車共享服務,由于其依托“互聯網+”,符合“低碳出行”的理念,已越來越多地引起了人們的關注.某部門為了對該城市共享單車加強監管,隨機選取了50人就該城市共享單車的推行情況進行問卷調査,并將問卷中的這50人根據其滿意度評分值(百分制)按照![]() 分成5組,請根據下面尚未完成并有局部污損的頻率分布表和頻率分布直方圖(如圖所示)解決下列問題:
分成5組,請根據下面尚未完成并有局部污損的頻率分布表和頻率分布直方圖(如圖所示)解決下列問題:
頻率分布表
組別 | 分組 | 頻數 | 頻率 |
第1組 |
| 8 | 0.16 |
第2組 |
|
| ▆ |
第3組 |
| 20 | 0.40 |
第4組 |
| ▆ | 0.08 |
第5組 |
| 2 |
|
合計 | ▆ | ▆ |
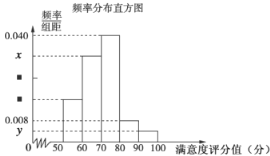
(1)求![]() 的值;
的值;
(2)若在滿意度評分值為![]() 的人中隨機抽取2人進行座談,求所抽取的2人中至少一人來自第5組的概率.
的人中隨機抽取2人進行座談,求所抽取的2人中至少一人來自第5組的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() ,
,![]() 是函數
是函數![]() 的圖象上任意兩點,若
的圖象上任意兩點,若![]() 為
為![]() ,
,![]() 的中點,且
的中點,且![]() 的橫坐標為
的橫坐標為![]() .
.
(1)求![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() ;
;
(3)已知數列![]() 的通項公式
的通項公式![]() (
(![]() ,
,![]() ),數列
),數列![]() 的前
的前![]() 項和為
項和為![]() ,若不等式
,若不等式![]() 對任意
對任意![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知動圓![]() 過點
過點![]() 且與直線
且與直線![]() 相切,圓心
相切,圓心![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)若![]() ,
,![]() 是曲線
是曲線![]() 上的兩個點且直線
上的兩個點且直線![]() 過
過![]() 的外心,其中
的外心,其中![]() 為坐標原點,求證:直線
為坐標原點,求證:直線![]() 過定點.
過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() :
:![]() 經過點
經過點![]() .
.
(1)求拋物線![]() 的方程及其準線方程;
的方程及其準線方程;
(2)設![]() 為原點,過拋物線
為原點,過拋物線![]() 的焦點作斜率不為0的直線
的焦點作斜率不為0的直線![]() 交拋物線
交拋物線![]() 于兩點
于兩點![]() ,
,![]() ,直線
,直線![]() 分別交直線
分別交直線![]() ,
,![]() 于點
于點![]() 和點
和點![]() .求證:以
.求證:以![]() 為直徑的圓經過
為直徑的圓經過![]() 軸上的兩個定點.
軸上的兩個定點.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com