
【題目】已知函數(shù)![]() .
.
(Ⅰ)求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅱ)若對于任意的![]() (
(![]() 為自然對數(shù)的底數(shù)),
為自然對數(shù)的底數(shù)),![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
【答案】(I)當![]() 時,
時, ![]() 的單調(diào)遞增區(qū)間為
的單調(diào)遞增區(qū)間為![]() ,無單調(diào)遞減區(qū)間;當
,無單調(diào)遞減區(qū)間;當![]() 時,
時,![]() 的單調(diào)遞增區(qū)間為
的單調(diào)遞增區(qū)間為![]() 和
和![]() ,單調(diào)遞減區(qū)間是
,單調(diào)遞減區(qū)間是![]() ;(II)
;(II)![]()
【解析】
(Ⅰ)求出![]() ,分兩種情況討論,在定義域內(nèi),分別令
,分兩種情況討論,在定義域內(nèi),分別令![]() 求得
求得![]() 的范圍,可得函數(shù)
的范圍,可得函數(shù)![]() 增區(qū)間,
增區(qū)間,![]() 求得
求得![]() 的范圍,可得函數(shù)
的范圍,可得函數(shù)![]() 的減區(qū)間;(Ⅱ)對
的減區(qū)間;(Ⅱ)對![]() 分四種情況討論,分別利用導(dǎo)數(shù)求出函數(shù)
分四種情況討論,分別利用導(dǎo)數(shù)求出函數(shù)![]() 最小值的表達式,令
最小值的表達式,令![]() 最小值不小于零,即可篩選出符合題意的
最小值不小于零,即可篩選出符合題意的![]() 的取值范圍.
的取值范圍.
(Ⅰ)![]() 的定義域為
的定義域為![]() .
.
![]()
![]() .
.
(1)當![]() 時,
時,![]() 恒成立,
恒成立,![]() 的單調(diào)遞增區(qū)間為
的單調(diào)遞增區(qū)間為![]() ,無單調(diào)遞減區(qū)間;
,無單調(diào)遞減區(qū)間;
(2)當![]() 時,由
時,由![]() 解得
解得![]() ,由
,由![]() 解得
解得![]() .
.
∴![]() 的單調(diào)遞增區(qū)間為
的單調(diào)遞增區(qū)間為![]() 和
和![]() ,單調(diào)遞減區(qū)間是
,單調(diào)遞減區(qū)間是![]() .
.
(Ⅱ)①當![]() 時,
時,![]() 恒成立,
恒成立,![]() 在
在![]() 上單調(diào)遞增,
上單調(diào)遞增,
∴![]() 恒成立,符合題意.
恒成立,符合題意.
②當![]() 時,由(Ⅰ)知,
時,由(Ⅰ)知,![]() 在
在![]() 、
、![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減.
上單調(diào)遞減.
(i)若![]() ,即
,即![]() 時,
時,![]() 在
在![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增.
上單調(diào)遞增.
∴對任意的實數(shù)![]() ,
,![]() 恒成立,只需
恒成立,只需![]() ,且
,且![]() .
.
而當![]() 時,
時,
![]() 且
且![]() 成立.
成立.
∴![]() 符合題意.
符合題意.
(ii)若![]() 時,
時,![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增.
上單調(diào)遞增.
∴對任意的實數(shù)![]() ,
,![]() 恒成立,只需
恒成立,只需![]() 即可,
即可,
此時![]() 成立,
成立,
∴![]() 符合題意.
符合題意.
(iii)若![]() ,
,![]() 在
在![]() 上單調(diào)遞增.
上單調(diào)遞增.
∴對任意的實數(shù)![]() ,
,![]() 恒成立,只需
恒成立,只需![]() ,
,
即![]() ,
,
∴![]() 符合題意.
符合題意.
綜上所述,實數(shù)![]() 的取值范圍是
的取值范圍是![]() .
.


 浙江之星課時優(yōu)化作業(yè)系列答案
浙江之星課時優(yōu)化作業(yè)系列答案 激活思維優(yōu)加課堂系列答案
激活思維優(yōu)加課堂系列答案科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系![]() 中,點
中,點![]() ,點
,點![]() 在
在![]() 軸上,點
軸上,點![]() 在
在![]() 軸非負半軸上,點
軸非負半軸上,點![]() 滿足:
滿足:![]()
(1)當點![]() 在
在![]() 軸上移動時,求動點
軸上移動時,求動點![]() 的軌跡C的方程;
的軌跡C的方程;
(2)設(shè)![]() 為曲線C上一點,直線
為曲線C上一點,直線![]() 過點
過點![]() 且與曲線C在點
且與曲線C在點![]() 處的切線垂直,
處的切線垂直,![]() 與C的另一個交點為
與C的另一個交點為![]() ,若以線段
,若以線段![]() 為直徑的圓經(jīng)過原點,求直線
為直徑的圓經(jīng)過原點,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知直線l:x﹣y+4=0和圓O:x2+y2=4,P是直線l上一點,過點P作圓C的兩條切線,切點分別為M,N.
(1)若PM⊥PN,求點P坐標;
(2)若圓O上存在點A,B,使得∠APB=60°,求點P的橫坐標的取值范圍;
(3)設(shè)線段MN的中點為Q,l與x軸的交點為T,求線段TQ長的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】我國是世界上嚴重缺水的國家,某市為了制定合理的節(jié)水方案,對居民用水情況進行調(diào)查,通過抽樣,獲得某年100為居民每人的月均用水量(單位:噸),將數(shù)據(jù)按照![]() 分成9組,制成了如圖所示的頻率分布直方圖.
分成9組,制成了如圖所示的頻率分布直方圖.
(1)求直方圖的![]() 的值;
的值;
(2)設(shè)該市有30萬居民,估計全市居民中月均用水量不低于3噸的人數(shù),說明理由.
(3)估計居民月用水量的中位數(shù).

查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】隨著我國中醫(yī)學的發(fā)展,藥用昆蟲的使用相應(yīng)愈來愈多.每年春暖以后至寒冬前,是昆蟲大量活動與繁殖季節(jié),易于采集各種藥用昆蟲.已知一只藥用昆蟲的產(chǎn)卵數(shù)![]() 與一定范圍內(nèi)的溫度
與一定范圍內(nèi)的溫度![]() 有關(guān),于是科研人員在3月份的31天中隨機挑選了5天進行研究,現(xiàn)收集了該種藥用昆蟲的5組觀測數(shù)據(jù)如下表:
有關(guān),于是科研人員在3月份的31天中隨機挑選了5天進行研究,現(xiàn)收集了該種藥用昆蟲的5組觀測數(shù)據(jù)如下表:
日期 | 2日 | 7日 | 15日 | 22日 | 30日 |
溫度 | 10 | 11 | 13 | 12 | 8 |
產(chǎn)卵數(shù) | 23 | 25 | 30 | 26 | 16 |
(1)從這5天中任選2天,記這兩天藥用昆蟲的產(chǎn)卵分別為![]() ,
,![]() ,求事件“
,求事件“![]() ,
,![]() 均不小于25”的概率;
均不小于25”的概率;
(2)科研人員確定的研究方案是:先從這五組數(shù)據(jù)中任選2組,用剩下的3組數(shù)據(jù)建立![]() 關(guān)于
關(guān)于![]() 的線性回歸方程,再對被選取的2組數(shù)據(jù)進行檢驗.
的線性回歸方程,再對被選取的2組數(shù)據(jù)進行檢驗.
(ⅰ)若選取的是3月2日與30日的兩組數(shù)據(jù),請根據(jù)3月7日、15日和22日這三天的數(shù)據(jù),求出![]() 關(guān)于
關(guān)于![]() 的線性回歸方程;
的線性回歸方程;
(ⅱ)若由線性回歸方程得到的估計數(shù)據(jù)與選出的檢驗數(shù)據(jù)的誤差均不超過2個,則認為得到的線性回歸方程是可靠的,試問(ⅰ)中所得的線性回歸方程是否可靠?
附:回歸直線的斜率和截距的最小二乘估計公式分別為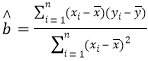 ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知{an}是等差數(shù)列,設(shè)數(shù)列{bn}的前n項和為Sn,且2bn=b1(1+Sn),bn≠0,又a2b2=4,a7+b3=11.
(1)求{an}和{bn}的通項公式;
(2)令cn=anbn(n∈N*),求{cn}的前n項和Tn
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() 平面
平面![]() ,
,![]() ,點
,點![]() 、
、![]() 分別在線段
分別在線段![]() 、
、![]() 上,且
上,且![]() ,其中
,其中![]() ,連接
,連接![]() ,延長
,延長![]() 與
與![]() 的延長線交于點
的延長線交于點![]() ,連接
,連接![]() .
.

(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 時,求二面角
時,求二面角![]() 的正弦值;
的正弦值;
(Ⅲ)若直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() 時,求
時,求![]() 值.
值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】下列說法中,錯誤的是( )
A. 若命題![]() ,
,![]() ,則命題
,則命題![]() ,
,![]()
B. “![]() ”是“
”是“![]() ”的必要不充分條件
”的必要不充分條件
C. “若![]() ,則
,則![]() 、
、![]() 中至少有一個不小于
中至少有一個不小于![]() ”的逆否命題是真命題
”的逆否命題是真命題
D. ![]() ,
,![]()
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com