
【題目】在平面直角坐標系![]() 中,點
中,點![]() ,點
,點![]() 在
在![]() 軸上,點
軸上,點![]() 在
在![]() 軸非負半軸上,點
軸非負半軸上,點![]() 滿足:
滿足:![]()
(1)當點![]() 在
在![]() 軸上移動時,求動點
軸上移動時,求動點![]() 的軌跡C的方程;
的軌跡C的方程;
(2)設![]() 為曲線C上一點,直線
為曲線C上一點,直線![]() 過點
過點![]() 且與曲線C在點
且與曲線C在點![]() 處的切線垂直,
處的切線垂直,![]() 與C的另一個交點為
與C的另一個交點為![]() ,若以線段
,若以線段![]() 為直徑的圓經過原點,求直線
為直徑的圓經過原點,求直線![]() 的方程.
的方程.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】
試題分析:(1)由點![]() 在
在![]() 軸上,點
軸上,點![]() 在
在![]() 軸非負半軸上且為動點,可設出設A(a,0),B(0,b),M(x,y),由關系
軸非負半軸上且為動點,可設出設A(a,0),B(0,b),M(x,y),由關系![]() ,將向量坐標代入可得動點
,將向量坐標代入可得動點![]() 的軌跡C的方程.
的軌跡C的方程.
(2)設Q(m,2m2), 直線![]() 過點
過點![]() 且與曲線C在點
且與曲線C在點![]() 處的切線垂直,可求出直線l的方程為y﹣2m2=
處的切線垂直,可求出直線l的方程為y﹣2m2=![]() (x﹣m),設
(x﹣m),設![]() ,聯立
,聯立![]() 與C的方程,并由韋達定理可得
與C的方程,并由韋達定理可得![]() ,
,![]() , (2m2)yR,2m2
, (2m2)yR,2m2![]() yR,又由線段
yR,又由線段![]() 為直徑的圓經過原點,所以
為直徑的圓經過原點,所以![]() ,即mxR+(2m2)yR=0,整理后可求出直線
,即mxR+(2m2)yR=0,整理后可求出直線![]() 的方程.
的方程.
試題解析:
解:(Ⅰ)設A(a,0),M(x,y),B(0,b),則![]() =(x﹣a,y),
=(x﹣a,y),![]() =(﹣a,b),
=(﹣a,b),![]() =(a,1)
=(a,1)
∵![]() =2
=2![]() ,∴有(x﹣a,y)=2(﹣a,b),即有x﹣a=﹣2a,y=2b,即x=﹣a,y=2b
,∴有(x﹣a,y)=2(﹣a,b),即有x﹣a=﹣2a,y=2b,即x=﹣a,y=2b
∵![]() ,∴有a(x﹣a)+y=0
,∴有a(x﹣a)+y=0
∴﹣x(x+x)+y=0,∴﹣2x2+y=0
即C的方程是y=2x2;
(Ⅱ)設Q(m,2m2),直線l的斜率為k,則y′=4x,∴k=![]()
∴直線l的方程為y﹣2m2=![]() (x﹣m)
(x﹣m)
與y=2x2聯立,消去y可得2x2+![]() x﹣2m2﹣
x﹣2m2﹣![]() =0,該方程必有兩根m與xR,且mxR=﹣m2﹣
=0,該方程必有兩根m與xR,且mxR=﹣m2﹣![]()
∴(2m2)yR=4(﹣m2﹣![]() )2
)2
∵![]() ,∴mxR+(2m2)yR=0,∴﹣m2﹣
,∴mxR+(2m2)yR=0,∴﹣m2﹣![]() +4(﹣m2﹣
+4(﹣m2﹣![]() )2=0,∴m=±
)2=0,∴m=±![]()
∴直線l的方程為![]() .
.


 金牌課堂練系列答案
金牌課堂練系列答案 三新快車金牌周周練系列答案
三新快車金牌周周練系列答案科目:高中數學 來源: 題型:
【題目】在正四面體A—BCD中,棱長為4,M是BC的中點,
點P在線段AM上運動(P不與A、M重合),過
點P作直線l⊥平面ABC,l與平面BCD交于點Q,
給出下列命題:
①BC⊥平面AMD ②Q點一定在直線DM上
③![]()
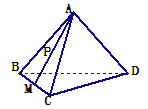
其中正確的是( )
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 是公差為正數的等差數列,其前
是公差為正數的等差數列,其前![]() 項和為
項和為![]() ,
,
且![]() ,
,![]()
(1)求數列![]() 的通項公式.
的通項公式.
(2)設數列![]() 滿足
滿足![]() ,
,![]()
①求數列![]() 的通項公式;
的通項公式;
②是否存在正整數![]() ,使得
,使得![]() ,
,![]() ,
,![]() 成等差數列?若存在,求出
成等差數列?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1為某省2018年1~4月快遞業務量統計圖,圖2是該省2018年1~4月快遞業務收入統計圖,下列對統計圖理解錯誤的是( )


A. 2018年1~4月的業務量,3月最高,2月最低,差值接近2000萬件
B. 2018年1~4月的業務量同比增長率均超過50%,在3月底最高
C. 從兩圖來看,2018年1~4月中的同一個月的快遞業務量與收入的同比增長率并不完全一致
D. 從1~4月來看,該省在2018年快遞業務收入同比增長率逐月增長
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是邊長為2的菱形,
是邊長為2的菱形,![]() ,側面
,側面![]() 為正三角形,側面
為正三角形,側面![]() 底面
底面![]() ,
,![]() 、
、![]() 分別為棱
分別為棱![]() 、
、![]() 的中點.
的中點.

(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)求證:平面![]() 平面
平面![]() ;
;
(Ⅲ)在棱![]() 上是否存在一點
上是否存在一點![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]()
![]() 的離心率為
的離心率為![]() ,點
,點![]() 為左焦點,過點
為左焦點,過點![]() 作
作![]() 軸的垂線交橢圓
軸的垂線交橢圓![]() 于
于![]() 、
、![]() 兩點,且
兩點,且![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)在圓![]() 上是否存在一點
上是否存在一點![]() ,使得在點
,使得在點![]() 處的切線
處的切線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 、
、![]() 兩點滿足
兩點滿足![]() ?若存在,求
?若存在,求![]() 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com