【題目】某商店經銷一種健身球，已知這種健身球的成本價為每個20元，市場調查發現，該種健身球每天的銷售量y（個）與銷售單價x（元）有如下關系：y=﹣20x+80（20≤x≤40），設這種健身球每天的銷售利潤為w元．
（1）求w與x之間的函數關系式；
（2）該種健身球銷售單價定為多少元時，每天的銷售利潤最大？最大利潤是多少元？
（3）如果物價部門規定這種健身球的銷售單價不高于28元，該商店銷售這種健身球每天要獲得150元的銷售利潤，銷售單價應定為多少元？
【答案】（1）w=﹣2x2+120x﹣1600；（2）銷售單價定為30元時，每天銷售利潤最大，最大銷售利潤200元；（3）25元
【解析】試題分析：（1）用每件的利潤
乘以銷售量即可得到每天的銷售利潤，即
然后化為一般式即可；
（2）把（1）中的解析式進行配方得到頂點式
然后根據二次函數的最值問題求解；
（3）求函數值為150所對應的自變量的值，即解方程
然后利用銷售價不高于每件28元確定
的值．
試題解析：（1）根據題意可得：
,
,
，
與之間的函數關系為：
；
（2）根據題意可得：
，
∵
，∴當
時，有最大值，最大值為200.
答：銷售單價定為30元時，每天銷售利潤最大，最大銷售利潤200元.
（3）當
時，可得方程
.
解得
，
∵
，∴
不符合題意，應舍去.
答：該商店銷售這種健身球每天想要獲得150元的銷售利潤，銷售單價定為25元.
開心快樂假期作業暑假作業西安出版社系列答案科目：初中數學 來源： 題型：
【題目】計算
（1）
（2）（+6）-（+12）+（+9．6）-（+7．6）
（3）5×
―
×
（4）（
）×(－60 )
（5）（2
)-(+10)+(-8
)-(+3)
（6）﹣14﹣（1﹣0.5）××[1﹣（﹣2）2]；
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】進價為每件40元的某商品，售價為每件50元時，每星期可賣出500件，市場調查反映：如果每件的售價每降價1元，每星期可多賣出100件，但售價不能低于每件42元，且每星期至少要銷售800件．設每件降價x元 （x為正整數），每星期的利潤為y元．
（1）求y與x的函數關系式并寫出自變量x的取值范圍；
（2）若某星期的利潤為5600元，此利潤是否是該星期的最大利潤？說明理由．
（3）直接寫出售價為多少時，每星期的利潤不低于5000元？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】雜技團進行雜技表演，演員從蹺蹺板右端A處彈跳到人梯頂端椅子B處，其身體(看成一點)的路線是拋物線
的一部分，如圖
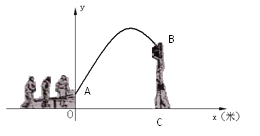
（1）求演員彈跳離地面的最大高度；
（2）已知人梯高BC＝3.4米，在一次表演中，人梯到起跳點A的水平距離是4米，問這次表演是否成功？請說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在正方形ABCD中，E、F分別為BC、CD邊上的兩個動點，∠EAF＝45°，下列幾個結論中：①EF＝BE＋DF；②MN2＝BM2＋DN2；③FA平分∠DFE；④連接MF，則△AMF為等腰直角三角形；⑤∠AMN＝∠AFE． 其中一定成立的結論有（ ）
A.2個B.3個C.4個D.5個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△ABC內接于⊙O，BC是直徑，⊙O的切線PA交CB的延長線于點P，OE∥AC交AB于點F，交PA于點E，連接BE．
（1）判斷BE與⊙O的位置關系并說明理由；
（2）若⊙O的半徑為4，BE=3，求AB的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示,在長方形ABCD中,AB=CD=8cm,AD=BC=6cm,點E是DC邊上一點,且CE=1cm,動點P從A點出發,沿折線A-D-E以acm/s的速度向終點E運動,運動時間為t秒,已知a是方程
的解.
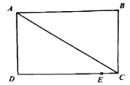
(1)求a的值；
(2)點P在運動過程中,請用t的式子表示△APC的面積；
(3)在點P運動的同時,有一動點Q從C點出發,沿折線C-D-A以1cm/s的速度向終點A運動,運動過程中,一個點停止運動時另一個點繼續向終點運動,當△APC和△AQC的面積相差6平方厘米時,求t的值.
查看答案和解析>>
科目：初中數學 來源： 題型：
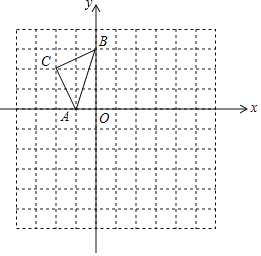
【題目】如圖，在已知的平面直角坐標系中，△ABC的頂點都在正方形網格的格點上，若A，B兩點的坐標分別是A（-1，0），B（0，3）．
（1）將△ABC繞原點O順時針旋轉90°得到△A1B1C1，畫出△A1B1C1；
（2）以點O為位似中心，與△ABC位似的△A2B2C2滿足A2B2：AB=2：1，請在網格內畫出△A2B2C2，并直接填寫△A2B2C2的面積為______．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀下列材料：
1637 年笛卡兒(R．Descartes，1596 1650)在其《幾何學》中，首次應用待定系數法將 4 次方程分解為兩個 2 次方程求解，并最早給出因式分解定理．
他認為，若一個高于二次的關于 x 的多項式能被 (
) 整除，則其一定可以分解為 () 與另外一個整式的乘積，而且令這個多項式的值為 0 時， x = a 是關于 x 的這個方程的一個根．
例如：多項式
可以分解為 (
) 與另外一個整式 M 的乘積，即 
令
時，可知 x =1 為該方程的一個根．
關于笛卡爾的“待定系數法”原理，舉例說明如下： 分解因式：
觀察知，顯然 x=1 時，原式 = 0 ，因此原式可分解為 () 與另一個整式的積．
令：
，則=
，因等式兩邊 x 同次冪的系數相等，則有：
，得
，從而
此時，不難發現 x= 1 是方程 
的一個根．
根據以上材料，理解并運用材料提供的方法，解答以下問題：
（1）若
是多項式
的因式，求 a 的值并將多項式分解因式；
（2）若多項式
含有因式及
，求a+ b 的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com