【題目】如圖，在平面直角坐標系中，已知C（3，4），以點C為圓心的圓與y軸相切．點A、B在x軸上，且OA=OB．點P為⊙C上的動點，∠APB=90°，則AB長度的最小值為（ ）
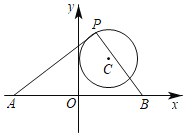
A.4B.3C.7D.8
閱讀快車系列答案科目：初中數學 來源： 題型：
【題目】如圖1，在矩形紙片
中，
，
，折疊紙片使
點落在邊
上的
處，拆痕為
．過點作
交于
，連接
．
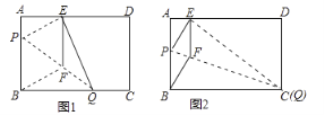
（1）求證：四邊形
為菱形；
（2）當點在邊上移動時，折痕的端點
、
也隨之移動；
①當點與點
重合時（如圖2），求菱形的邊長；
②若限定、分別在邊
、
上移動，求
的內切圓半徑的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為拓寬學生視野，促進書本知識和生活經驗的深度融合，我市某中學決定組織部分班級開展研學旅行活動，在參加此次活動的師生中，若每位老師帶
名學生，還剩
名學生沒人帶；若每位老師帶
名學生，則有一位老師少帶
名學生．現有甲、乙兩種大客車，它們的載客量和租金如下表所示．
甲種客車 | 已和客車 | |
載客量（人/量） |
|
|
租金（元/輛） |
|
|
學校計劃此次研學旅行活動的租車總費用不超過
元，為了安全，每輛客車上至少要有
名老師．
（1）參加此次研學旅行活動的老師和學生各有多少人？
（2）既要保證所有師生都有車坐，又要保證每輛客車上至少要有名老師，可求得租用客車總數為______輛．
（3）在（2）的條件下，你能得出哪幾種不同的租車方案？其中哪種租車方案最省錢？請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，ABCD是一塊邊長為4米的正方形苗圃，園林部門擬將其改造為矩形AEFG的形狀，其中點E在AB邊上，點G在AD的延長線上，DG= 2BE．設BE的長為x米，改造后苗圃AEFG的面積為y平方米．
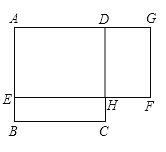
（1）求y與x之間的函數關系式（不需寫自變量的取值范圍）；
（2）根據改造方案，改造后的矩形苗圃AEFG的面積與原正方形苗圃ABCD的面積相等，請問此時BE的長為多少米？
查看答案和解析>>
科目：初中數學 來源： 題型：
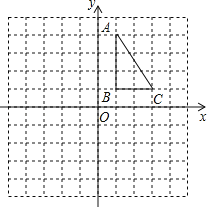
【題目】如圖，正方形網格中，每個小正方形的邊長都是一個單位長度，在平面直角坐標系內，△ABC的三個頂點坐標分別為A（1，4），B（1，1），C（3，1）．
（1）畫出△ABC關于x軸對稱的△A1B1C1；
（2）畫出△ABC繞點O逆時針旋轉90°后的△A2B2C2；
（3）在（2）的條件下，求線段BC掃過的面積（結果保留π）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△OAB中，頂點O（0，0），A（﹣2，3），B（2，3），將△OAB與正方形ABCD組成的圖形繞點O順時針旋轉，每次旋轉90°，則第2020次旋轉結束時，點D的坐標為（ ）
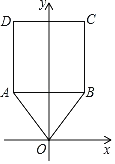
A.（﹣2，7）B.（7，2）C.（2，﹣7）D.（﹣7，﹣2）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系xOy中，拋物線y = ax2+ bx + c經過A、B、C三點，已知點A（-3，0），B（0，3），C（1，0）．
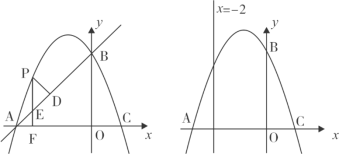
（1）求此拋物線的解析式；
（2）點P是直線AB上方的拋物線上一動點，（不與點A、B重合），過點P作x軸的垂線，垂足為F，交直線AB于點E，作PD⊥AB于點D．動點P在什么位置時，△PDE的周長最大，求出此時P點的坐標；
（3）在直線x = -2上是否存在點M，使得∠MAC = 2∠MCA，若存在，求出M點坐標．若不存在，說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】我們知道：四邊形具有不穩定性．如圖，在平面直角坐標系中，將邊長為4的菱形
的邊
固定在
軸上，開始時
，現把菱形向左推，使點
落在
軸正半軸上的點
處，則下列說法中錯誤的是（ ）
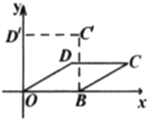
A.點
的坐標為
B.
C.點移動的路徑長度為4個單位長度D.
垂直平分
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系
中，拋物線
與直線
交于點
，且點的橫坐標為
．
（1）請用
的代數式表示
；
（2）點
在直線
上，點的橫坐標為
，點
的坐標為
．
①若拋物線
過點，求該拋物線的解析式；
②若拋物線與線段
恰有一個交點，直接寫出的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
