Question

【題目】如圖，在平面直角坐標系中，菱形OBCD的邊OB在x軸上，反比例函數y= （x＞0）的圖象經過菱形對角線的交點A，且與邊BC交于點F，點A的坐標為（4，2）．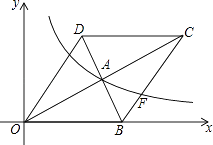

（1）求反比例函數的表達式；
（2）求點F的坐標．

Answer 1

【答案】
（1）解：∵反比例函數y= 的圖象經過點A，A點的坐標為（4，2），

∴k=2×4=8，

∴反比例函數的解析式為y=

（2）解：過點A作AM⊥x軸于點M，過點C作CN⊥x軸于點N，

由題意可知，CN=2AM=4，ON=2OM=8，

∴點C的坐標為C（8，4），

設OB=x，則BC=x，BN=8﹣x，

在Rt△CNB中，x2﹣（8﹣x）2=42，

解得：x=5，

∴點B的坐標為B（5，0），

設直線BC的函數表達式為y=ax+b，直線BC過點B（5，0），C（8，4），

∴ ，

解得： ，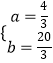

∴直線BC的解析式為y= x+ ，

根據題意得方程組 ，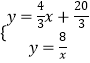

解此方程組得： 或

∵點F在第一象限，

∴點F的坐標為F（6， ）．

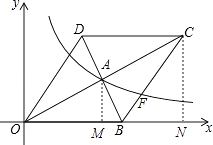
【解析】（1）將點A的坐標代入到反比例函數的一般形式后求得k值即可確定函數的解析式；（2）過點A作AM⊥x軸于點M，過點C作CN⊥x軸于點N，首先求得點B的坐標，然后求得直線BC的解析式，求得直線和拋物線的交點坐標即可．本題考查了反比例函數圖象上的點的特點、待定系數法確定反比例函數的解析式等知識，解題的關鍵是能夠根據點C的坐標確定點B的坐標，從而確定直線的解析式．
【考點精析】根據題目的已知條件，利用菱形的性質的相關知識可以得到問題的答案，需要掌握菱形的四條邊都相等；菱形的對角線互相垂直，并且每一條對角線平分一組對角；菱形被兩條對角線分成四個全等的直角三角形；菱形的面積等于兩條對角線長的積的一半．