
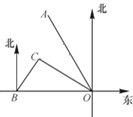
【題目】如圖所示,港口B位于港口O正西方向120 km處,小島C位于港口O北偏西60°的方向.一艘游船從港口O出發,沿OA方向(北偏西30°)以v km/h的速度駛離港口O,同時一艘快艇從港口B出發,沿北偏東30°的方向以60 km/h的速度駛向小島C,在小島C用1 h加裝補給物資后,立即按原來的速度給游船送去.
(1)快艇從港口B到小島C需要多長時間?
(2)若快艇從小島C到與游船相遇恰好用時1h,求v的值及相遇處與港口O的距離.
【答案】(1)快艇從港口B到小島C需要的時間為1小時;(2) 當v=20時,OE=60km;當v=40時,OE=120km.
【解析】
試題(1)要求B到C的時間,已知其速度,則只要求得BC的路程,再利用路程公式即可求得所需的時間;
(2)過C作CD⊥OA,垂足為D,設相會處為點E.求出OC=OBcos30°=![]() ,CD=
,CD=![]() OC=
OC=![]() ,OD=OCcos30°=90,則DE=90﹣3v.在直角△CDE中利用勾股定理得出
,OD=OCcos30°=90,則DE=90﹣3v.在直角△CDE中利用勾股定理得出![]() ,即
,即![]() ,解方程求出v=20或40,進而求出相遇處與港口O的距離.
,解方程求出v=20或40,進而求出相遇處與港口O的距離.
試題解析:(1)∵∠CBO=60°,∠COB=30°,∴∠BCO=90°.在Rt△BCO中,∵OB=120,∴BC=![]() OB=60,∴快艇從港口B到小島C的時間為:60÷60=1(小時);
OB=60,∴快艇從港口B到小島C的時間為:60÷60=1(小時);
(2)過C作CD⊥OA,垂足為D,設相會處為點E.則OC=OBcos30°=![]() ,CD=
,CD=![]() OC=
OC=![]() ,OD=OCcos30°=90,∴DE=90﹣3v.∵CE=60,
,OD=OCcos30°=90,∴DE=90﹣3v.∵CE=60,![]() ,∴
,∴![]() ,∴v=20或40,∴當v=20km/h時,OE=3×20=60km,當v=40km/h時,OE=3×40=120km.
,∴v=20或40,∴當v=20km/h時,OE=3×20=60km,當v=40km/h時,OE=3×40=120km.


科目:初中數學 來源: 題型:
【題目】某單位要印刷“市民文明出行,遵守交通安全”的宣傳材料.甲印刷廠提出:每份材料收2元印刷費,另收1000元的制版費;乙印刷廠提出:每份材料收3元印刷費,不收制版費.
(1)分別寫出兩個印刷廠的收費![]() ,
,![]() (元)與印制數量
(元)與印制數量![]() (份)之間的關系式(不用寫出自變量的取值范圍);
(份)之間的關系式(不用寫出自變量的取值范圍);
(2)在同一坐標系內畫出它們的圖象,并求出當印制多少份宣傳材料,兩個印刷廠的印制費用相同?此時費用為多少?
(3)結合圖象回答:在印刷品數量相同的情況下選哪家印刷廠印制省錢?
查看答案和解析>>
科目:初中數學 來源: 題型:
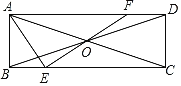
【題目】如圖,在矩形ABCD中,AB=1,BC=3,AC和BD交于點O,點E是邊BC上的動點(不與點B,C重合),連接EO并延長交AD于點F,連接AE,若△AEF是等腰三角形,則DF的長為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料,然后回答問題:
已知a>0,S1=![]() ,S2=﹣S1﹣1,S3=
,S2=﹣S1﹣1,S3=![]() ,S4=﹣S3﹣1,S5=
,S4=﹣S3﹣1,S5=![]() ,….當n為大于1的奇數時,Sn=
,….當n為大于1的奇數時,Sn=![]() ;當n為大于1的偶數時,Sn=﹣Sn﹣1﹣1.直接寫出S2020=_____(用含a的代數式表示);計算:S1+S2+S3+…+S2022=_____.
;當n為大于1的偶數時,Sn=﹣Sn﹣1﹣1.直接寫出S2020=_____(用含a的代數式表示);計算:S1+S2+S3+…+S2022=_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,一次函數![]() 與反比例函數
與反比例函數![]() 的圖象相交于
的圖象相交于![]() 兩點,過點
兩點,過點![]() 作
作![]() 軸于點
軸于點![]() ,
,![]() ,
,![]() ,
,![]() 點的坐標為
點的坐標為![]() .
.
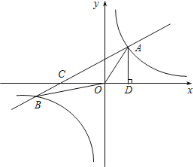
(1)求一次函數和反比例函數的表達式;
(2)求![]() 的面積;
的面積;
(3)![]() 是
是![]() 軸上一點,且
軸上一點,且![]() 是等腰三角形,請直接寫出所有符合條件的
是等腰三角形,請直接寫出所有符合條件的![]() 點坐標.
點坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A與點B關于原點對稱,點C在第四象限,∠ACB=90°.點D是![]() 軸正半軸上一點,AC平分∠BAD,E是AD的中點,反比例函數
軸正半軸上一點,AC平分∠BAD,E是AD的中點,反比例函數![]() (
(![]() )的圖象經過點A,E.若△ACE的面積為6,則
)的圖象經過點A,E.若△ACE的面積為6,則![]() 的值為( )
的值為( )
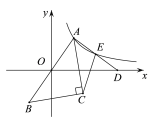
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了了解學生參加體育活動的情況,學校對學生進行隨機抽樣調查,其中一個問題是“你平均每天參加體育活動的時間是多少”,共有4個選項:A 1.5小時以上;B 1~1.5小時;C 0.5~1小時;D 0.5小時以下.圖1、2是根據調查結果繪制的兩幅不完整的統計圖,請你根據統計圖提供的信息,解答以下問題:

(1)本次一共調查了多少名學生?
(2)在圖1中將選項B的部分補充完整;
(3)若該校有3000名學生,你估計全校可能有多少名學生平均每天參加體育活動的時間在0.5小時以下.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com