
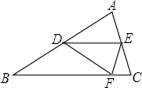
【題目】如圖,△ABC紙片中,AB=BC>AC,點(diǎn)D是AB邊的中點(diǎn),點(diǎn)E在邊AC上,將紙片沿DE折疊,使點(diǎn)A落在BC邊上的點(diǎn)F處.則下列結(jié)論成立的個(gè)數(shù)有( )①△BDF是等腰直角三角形;②∠DFE=∠CFE;③DE是△ABC的中位線(xiàn);④BF+CE=DF+DE.
A. 1個(gè)B. 2個(gè)C. 3個(gè)D. 4個(gè)
【答案】B
【解析】
根據(jù)題意可知△DFE是△DAE對(duì)折的圖形,所以全等,故AD=DF,而AD=BD,所以BD=DF,但是∠B不一定等于45°,所以△BDF不一定是等腰直角三角形,①不成立;結(jié)合①中的結(jié)論,BD=DF,而∠ADE=∠FDE,∠ADF=∠DBF+∠DFB,可證∠BFD=∠EDF,故DE∥BC,即DE是△ABC的中位線(xiàn),③成立;若③成立,利用△ADE≌△FDE,DE∥BC,∠AEF=∠EFC+∠ECF,可證∠DFE=∠CFE,②成立;根據(jù)折疊以及中位線(xiàn)定理得右邊=AB,要和左邊相等,則需CE=CF,則△CEF應(yīng)是等邊三角形,顯然不一定,故④不成立.
解:①根據(jù)折疊知AD=DF,所以BD=DF,即一定是等腰三角形.因?yàn)椤?/span>B不一定等于45°,所以①錯(cuò)誤;
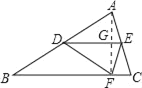
②連接AF,交DE于G,根據(jù)折疊知DE垂直平分AF,又點(diǎn)D是AB邊的中點(diǎn),在△ABF中,根據(jù)三角形的中位線(xiàn)定理,得DG∥BF.進(jìn)一步得E是AC的中點(diǎn).由折疊知AE=EF,則EF=EC,得∠C=∠CFE.又∠DFE=∠A=∠C,所以∠DFE=∠CFE,正確;
③在②中已證明正確;
④根據(jù)折疊以及中位線(xiàn)定理得右邊=AB,要和左邊相等,則需CE=CF,則△CEF應(yīng)是等邊三角形,顯然不一定,錯(cuò)誤.
故選:B.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
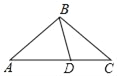
【題目】如圖,在△ABC中,BA=BC=4,∠A=30°,D是AC上一動(dòng)點(diǎn),
(Ⅰ)AC的長(zhǎng)=_____;
(Ⅱ)BD+![]() DC的最小值是_____.
DC的最小值是_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
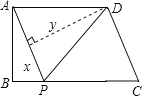
【題目】如圖,四邊形ABCD中,AD∥BC,∠ABC=90°,AB=3,AD=4,BC=![]() ,動(dòng)點(diǎn)P從A點(diǎn)出發(fā),按A→B→C的方向在AB和BC上移動(dòng),記PA=x,點(diǎn)D到直線(xiàn)PA的距離為y,則y關(guān)于x的函數(shù)圖象大致是( )
,動(dòng)點(diǎn)P從A點(diǎn)出發(fā),按A→B→C的方向在AB和BC上移動(dòng),記PA=x,點(diǎn)D到直線(xiàn)PA的距離為y,則y關(guān)于x的函數(shù)圖象大致是( )
A. 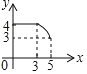 B.
B. 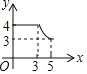
C. 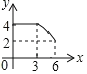 D.
D. 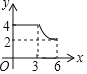
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某出租汽車(chē)公司有出租車(chē)100輛,平均每天每車(chē)消耗的汽油費(fèi)為80元,為了減少環(huán)境污染,市場(chǎng)推出一種叫“CNG”的改燒汽油為天然汽的裝置,每輛車(chē)改裝價(jià)格為4000元.公司第一次改裝了部分車(chē)輛后核算:已改裝后的車(chē)輛每天的燃料費(fèi)占剩下未改裝車(chē)輛每天燃料費(fèi)用的15%,公司第二次再改裝同樣多的車(chē)輛后,所有改裝后的車(chē)輛每天的燃料費(fèi)占剩下未改裝車(chē)輛每天燃料費(fèi)用的40%.問(wèn):
(1)公司共改裝了多少輛出租車(chē)?改裝后的每輛出租車(chē)平均每天的燃料費(fèi)比改裝前的燃料費(fèi)下降了百分之多少?
(2)若公司一次性將全部出租車(chē)改裝,多少天后就可以從節(jié)省的燃料費(fèi)中收回成本?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某校積極參與垃圾分類(lèi)活動(dòng),以班級(jí)為單位收集可回收的垃圾,下面是七年級(jí)各班一周收集的可回收垃圾的質(zhì)量頻數(shù)表和頻數(shù)直方圖(每組含前一個(gè)邊界值,不含后一個(gè)邊界值).
某校七年級(jí)各班一周收集的可回收垃圾的質(zhì)量頻數(shù)表
組別(kg) | 頻數(shù) |
4.0~4.5 | 2 |
4.5~5.0 | a |
5.0~5.5 | 3 |
5.5~6.0 | 1 |
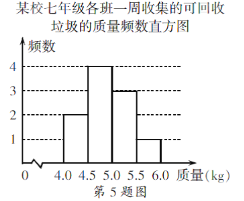
(1)求a的值;
(2)已知收集的可回收垃圾以0.8元/kg被回收,該年級(jí)這周收集的可回收垃圾被回收后所得的金額能否達(dá)到50元.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
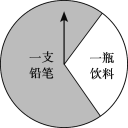
【題目】某商場(chǎng)有一個(gè)可以自由轉(zhuǎn)動(dòng)的圓形轉(zhuǎn)盤(pán)(如圖).規(guī)定:顧客購(gòu)物100元以上可以獲得一次轉(zhuǎn)動(dòng)轉(zhuǎn)盤(pán)的機(jī)會(huì),當(dāng)轉(zhuǎn)盤(pán)停止時(shí),指針落在哪一個(gè)區(qū)域就獲得相應(yīng)的獎(jiǎng)品(指針指向兩個(gè)扇形的交線(xiàn)時(shí),當(dāng)作指向右邊的扇形).下表是活動(dòng)進(jìn)行中的一組統(tǒng)計(jì)數(shù)據(jù):
轉(zhuǎn)動(dòng)轉(zhuǎn)盤(pán)的次數(shù)n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“鉛筆”的次數(shù)m | 68 | 111 | 136 | 345 | 546 | 701 |
落在“鉛筆”的頻率 (結(jié)果保留小數(shù)點(diǎn)后兩位) | 0.68 | 0.74 | 0.68 | 0.69 | 0.68 | 0.70 |
(1)轉(zhuǎn)動(dòng)該轉(zhuǎn)盤(pán)一次,獲得鉛筆的概率約為_______;(結(jié)果保留小數(shù)點(diǎn)后一位)
(2)鉛筆每只0.5元,飲料每瓶3元,經(jīng)統(tǒng)計(jì)該商場(chǎng)每天約有4000名顧客參加抽獎(jiǎng)活動(dòng),請(qǐng)計(jì)算該商場(chǎng)每天需要支出的獎(jiǎng)品費(fèi)用;
(3)在(2)的條件下,該商場(chǎng)想把每天支出的獎(jiǎng)品費(fèi)用控制在3000元左右,則轉(zhuǎn)盤(pán)上“一瓶飲料”區(qū)域的圓心角應(yīng)調(diào)整為______度.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
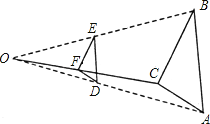
【題目】按如下方法,將△ABC的三邊縮小的原來(lái)的![]() ,如圖,任取一點(diǎn)O,連AO、BO、CO,并取它們的中點(diǎn)D、E、F,得△DEF,則下列說(shuō)法正確的個(gè)數(shù)是( )
,如圖,任取一點(diǎn)O,連AO、BO、CO,并取它們的中點(diǎn)D、E、F,得△DEF,則下列說(shuō)法正確的個(gè)數(shù)是( )
①△ABC與△DEF是位似圖形②△ABC與△DEF是相似圖形
③△ABC與△DEF的周長(zhǎng)比為1:2④△ABC與△DEF的面積比為4:1.
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,直線(xiàn)AB和拋物線(xiàn)的交點(diǎn)是A(0,-3),B(5,9),已知拋物線(xiàn)的頂點(diǎn)D的橫坐標(biāo)是2.

(1)求拋物線(xiàn)的解析式及頂點(diǎn)坐標(biāo);
(2)在![]() 軸上是否存在一點(diǎn)C,與A,B組成等腰三角形?若存在,求出點(diǎn)C的坐標(biāo),若不存在,請(qǐng)說(shuō)明理由;
軸上是否存在一點(diǎn)C,與A,B組成等腰三角形?若存在,求出點(diǎn)C的坐標(biāo),若不存在,請(qǐng)說(shuō)明理由;
(3)在直線(xiàn)AB的下方拋物線(xiàn)上找一點(diǎn)P,連接PA,PB使得△PAB的面積最大,并求出這個(gè)最大值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
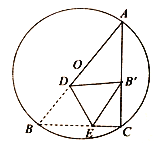
【題目】如圖,![]() 內(nèi)接于
內(nèi)接于![]() ,
,![]() 為
為![]() 的直徑,
的直徑,![]() ,
,![]() ,
,![]() 、
、![]() 分別是邊
分別是邊![]() 、
、![]() 上的兩個(gè)動(dòng)點(diǎn)(不與端點(diǎn)
上的兩個(gè)動(dòng)點(diǎn)(不與端點(diǎn)![]() 、
、![]() 、
、![]() 重合),將
重合),將![]() 沿
沿![]() 折疊,點(diǎn)
折疊,點(diǎn)![]() 的對(duì)應(yīng)點(diǎn)
的對(duì)應(yīng)點(diǎn)![]() 恰好落在線(xiàn)段
恰好落在線(xiàn)段![]() 上(包含端點(diǎn)
上(包含端點(diǎn)![]() 、
、![]() ),若
),若![]() 為等腰三角形,則
為等腰三角形,則![]() 的長(zhǎng)為__.
的長(zhǎng)為__.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com